排队论在钢铁企业中的应用研究
梁素梅 陈娜

摘要:通过对钢铁企业中受铁罐转炉兑铁作业物流过程的解析,在排队论的基础上,分别建立了转炉兑铁作业的单队列和多队列排队系统;计算出两种排队系统的主要数量指标;并讨论了转炉数量对平均等待受铁罐数(包括节省的)和受铁罐平均等待服务时间(包括节省的)的影响。研究表明单队列(M/M/N)的排队系统可为钢铁企业物流优化提供理论参考。
Abstract: Based on the analysis of hot metal charging ladle's operation logistics process in the iron and steel enterprises, on the basis of the queuing theory, the single-queue and multi-user queuing systems of hot metal charging ladle operation were established respectively; the main quantitative indicators of the two queuing systems were calculated. And it discussed the impact of the number of hot metal charging on the average waiting for the number of hot metal ladles (including savings) and the average waiting time for hot metal ladles (including savings). Research shows that the single queue can provide theoretical reference for the steel enterprises' material flow optimization.
關键词:高炉-转炉区段;兑铁;排队论;M/M/N
Key words: BF-BOF region;hot metal charging;queuing theory;M/M/N
中图分类号:F426 文献标识码:A 文章编号:1006-4311(2020)02-0105-04
0 引言
随着产钢量的迅速增长,进一步节约能源,降低生产和经营成本,俨然成为各钢铁企业优先考虑的问题。钢铁企业中从总体上研究钢铁厂内部结构的新思路被不少有识之士提出,也就是说在开发和采用钢铁生产新技术的同时,从宏观分析钢铁企业生产流程。从而可对钢铁企业流程进行整体优化和节能增效。鲜少涉及用数学方法分解和研究钢铁企业各物流环节。在此思路下本文通过对国内某大型钢铁企业中受铁罐转炉兑铁作业环节进行物流分析,在排队论的基础上,分别建立了转炉兑铁作业的单队列和多队列排队系统;计算出两种排队系统的主要数量指标;并对转炉数量与平均等待受铁罐数(包括节省的)和受铁罐平均等待服务时间(包括节省的)关系进行讨论。
1 理论分析
1.1 受铁罐转炉兑铁作业排队系统
受铁罐转炉兑铁作业实质上是一个排队系统,其基本结构由受铁罐、转炉兑铁和排队规则三个部分组成。受铁罐转炉兑铁排队系统的主要成分是受铁罐和转炉。在此作业环节中,受铁罐可看成排队系统中的输入过程,一开始受铁罐在汽车的运输或火车头的牵引下成批到达各个调车场排队等待调派到转炉兑铁,然后受铁罐到达检罐站排队等待检罐,受铁罐车检罐完后按队列在转炉处接受兑铁。
1.2 单多队列的排队系统的数学指标
在受铁罐转炉兑铁作业排队系统中,“单队列多转炉兑铁”的排队方式即M/M/N(见图1):受铁罐单个到达,相继到达转炉的时间间隔服从参数为λ的负指数分布;受铁罐在每个转炉的兑铁时间服从参数为μ的负指数分布且相互独立;共有N个转炉对受铁罐进行兑铁。和“多队列多转炉兑铁”的排队方式是指N个M/M/1(见图2)的排队系统:只有一个转炉对受铁罐进行兑铁时就是 M/M/1;N个M/M/1是指:有N个独立的转炉兑铁(M/M/1)排队系统。
通过上述排队论的相关知识可知:表示系统M/M/1和M/M/N在t时刻的受铁罐数。则{N1(t),t?叟0},{N2(t),t?叟0}均是状态有限的生死过程,平稳解存在[1,2]。假设受铁罐泊松到达的参数是?姿,转炉兑铁时间参数是?滋,现在给出这两种排队系统的主要稳定态数学指标。
1.2.1 受铁罐单队多转炉兑铁排队系统(M/M/N)
受铁罐单队多转炉兑铁排队系统:受铁罐单个到达,相继到达转炉的时间间隔服从参数为λ的负指数分布,此排队系统中共有N个转炉可以对受铁罐进行兑铁,每个转炉兑铁时间服从参数为μ的负指数分布且彼此独立。一旦有受铁罐到达,则空闲的转炉就对受铁罐进行兑铁,不然则排成一个等待时间为无限的队列等待兑铁。其次对此排队系统的平稳分布进行讨论。对个数为N的多转炉兑铁排队系统,有M/M/N:设转炉兑铁利用率为?籽,则?籽=;其中Pn(N=n)(n=1,2,3,…)表示当系统达到平衡状态后,队长N的概率分布。则当?籽<1时,受铁罐单队多转炉兑铁排队系统存在平稳分布,记为P0,P1,P2…,可得此系统状态的平衡(即输入流=输出流)方程为:
其中。由此可推导出此系统的主要的稳定态数学指标:
等待兑铁的平均受铁罐数:
平均受铁罐数(包括等待的和服务的):
受铁罐平均等待时间:
受铁罐的平均逗留时间:
1.2.2 受铁罐多队多转炉兑铁排队系统(N个M/M/1)
单个转炉兑铁系统M/M/1:受铁罐的相继到达转炉的时间服从参数为λ的负指数分布,转炉兑铁时间同样也服从参数为μ的负指数分布,且转炉台数为一台的空间无限允许无限排队的最简单的排队系统。N个M/M/1是指:有N个独立相同的M/M/1系统。
M/M/1:设兑铁强度为?籽,则?籽=;=其中P0=1-?籽,n=1、2,…。当?籽<1时,此系统存在平稳分布,记为P0,P1,P2…,并推导出系统状态的平衡方程为:(6
据此,主要的稳定态数学指标如下:
平均受铁罐数(包括等待的和服务的):
等待兑铁的平均受铁罐数:
每个受铁罐平均等待时间:
每个受铁罐的平均逗留时间:
1.3 单多队列排队系统主要数学指标对比
如果把到达的受铁罐均匀分流到N个M/M/1/排队系统中去,每个子流强度为,依然还是泊松流。现在比较N个单独的转炉兑铁的排队系统与具有N个转炉兑铁的排队系统的主要数学指标。假设每个转炉兑铁率都是?滋,且?籽=<1。则有
①兑铁强度。M/M/N系统?籽=。N个M/M/1系统?籽==,相同。
②转炉兑铁空闲概率。
因此。而M/M/1系统。从而M/M/N系统空闲概率小于N个M/M/1系统空闲概率。
③受铁罐等待概率。
M/M/N系统受铁罐等待概率为
但
所以 (11)
但是在N个M/M/1系统,系统受铁罐排队等待概率,根据上述得到N个M/M/1系统等待机会大。
④等待受铁罐数。
M/M/N排队系统 (12)
而N个M/M/1系统
得到N个M/M/1系统受铁罐等待罐数多。
⑤受铁罐数。
M/M/N排队系统(13)
N个M/M/1系统平均受铁罐数是M/M/N排队系统受铁罐数的N倍,
为(14)
但是 (15)
为N个M/M/1系统的受铁罐数。
⑥受铁罐等待兑铁时间。
M/M/N系统受铁罐平均等待兑铁时间
而N个M/M/1系统 由(16)、(17)知,即M/M/N系统受铁罐等待兑铁时间短。
综上六个方面比较:单多队列排队系统,在受铁罐转炉兑铁作业中,除空闲概率P0外,单队列排队系统的其它主要数学指标都优于多队列排队系统的。然而受铁罐多队列排队系统的空闲概率小,也就表明此系统的效力高,据此合营比单干产生的效益确实高一些。式(2)到式(10)的数学指标越小,那么排队系统的性能反而会越好。式(2)到式(5)与式(7)到式(10)解析比较并结合上述六个方面得出前者优于后者,因此受铁罐单队列排队系统比多队列排队系统更优。
2 案例实施
某大型钢铁企业用受铁罐“一罐到底”模式代替现有的“鱼雷罐-兑铁包”模式。据相关文献报道[3],用100t的受铁罐来盛接铁水,则也要用对应公称容量为100t的转炉,用一车3罐的方式来进行运输。则受铁罐泊松到达的参数?姿为3罐/时,那么受铁罐到达时间间隔则服从平均时间为1/3时的负指数分布。受铁罐转炉兑铁作业服从平均服务时间为15分钟的负指数分布,即?滋为1/15罐/分钟。
2.1 受铁罐单多队列排队系统的主要数量指标
受铁罐排队系统主要由输入过程(受铁罐)、受铁罐到达规则、受铁罐排队规则、转炉结构、兑铁时间以及兑铁规则等要素来组成。在钢铁企业受铁罐转炉兑铁作业环节中,受铁罐单队列M/M/N排队系统:表示在此作业中的受铁罐到达间隔时间(但参数一般不同)、受铁罐服务时间服从负指数分布,且有N个转炉的排队系统;受铁罐多队列N个M/M/1表示受铁罐到达间隔时间和服务时间均服从负指数分布且只有一个转炉的排队系统[1,2,4]。排队系统的评价指标分为受铁罐和转炉两方面。可用排队时间、等待队长、队长、堵塞概率、排队的概率等来作为判断受铁罐的主要数量指标。与转炉相关的数量指标主要有转炉利用率、排队区利用率、受铁罐兑铁能力等。对双方利益进行综合考虑,通过对受铁罐转炉兑铁排队系统的主要数量指标(等待概率P、平均等待的受铁罐数Lq、进入车轨的平均受铁罐数Ls、每个受铁罐在车轨内的平均逗留时间Ws和平均等待服务时间Wq以及转炉兑铁繁忙率/空闲率等)对排队系统进行评价。用单多队列排队系统的主要数量指标对N=2(即转炉台数=2)进行计算,得到结果表1。
2.2 单多队列排队系统下转炉数量对平均等待受铁罐数Lq的影响
单多队列排队模式下,转炉数量与平均等待受铁罐数Lq的关系见图3。单队列排队模式下,随着转炉数量的增多,平均进入车轨中的等待受铁罐数目越来越少;并且对于多队列,随着转炉数量增多,平均等待受铁罐Lq=2.25罐不变。
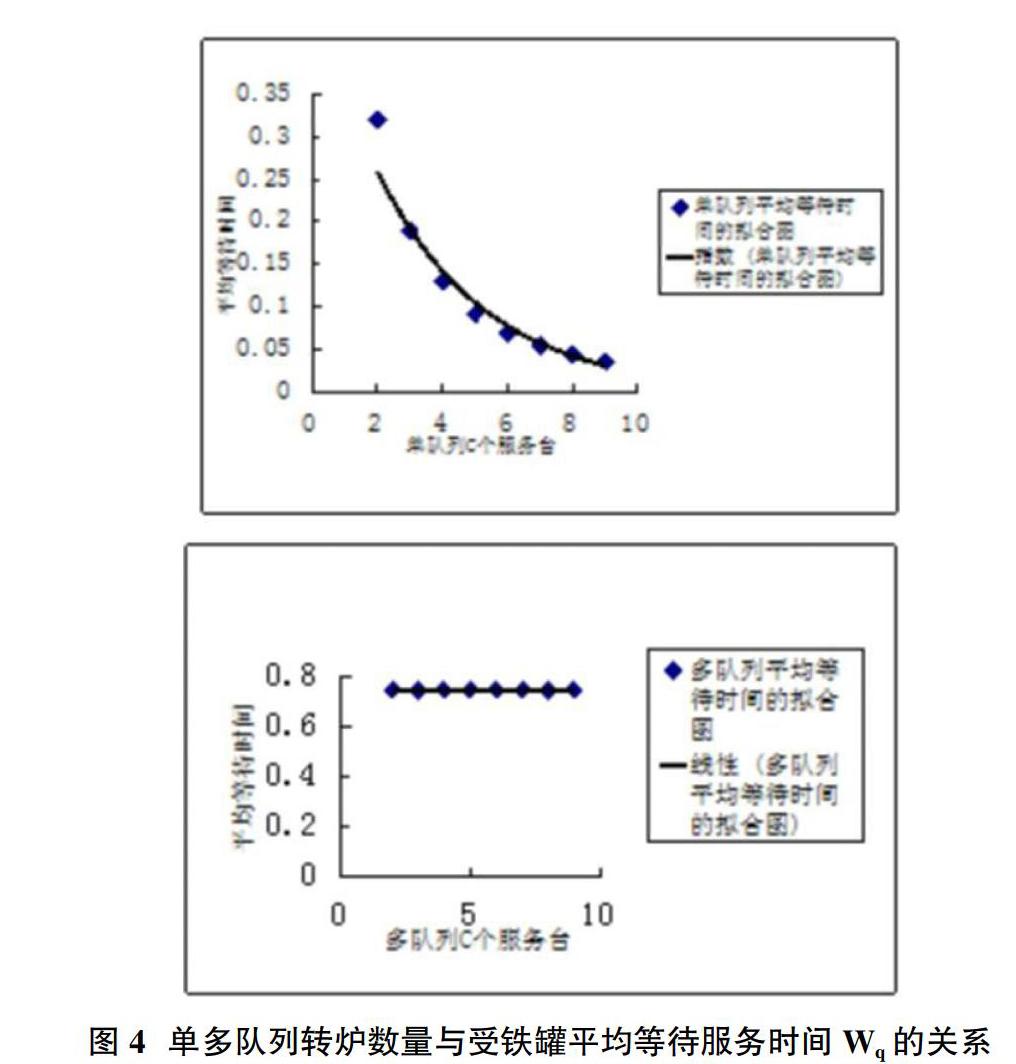
2.3 单多队列排队系统下转炉数量对受铁罐平均等待服务时间Wq的影响
单多队列排队模式下,转炉数量与受铁罐平均等待服务时间Wq的关系见图4。单队列排队模式下,隨着转炉数量的增多,受铁罐平均等待服务时间也越来越短;并且对于多队列,随着转炉数量的增多,受铁罐平均等待服务时间都是0.75h。
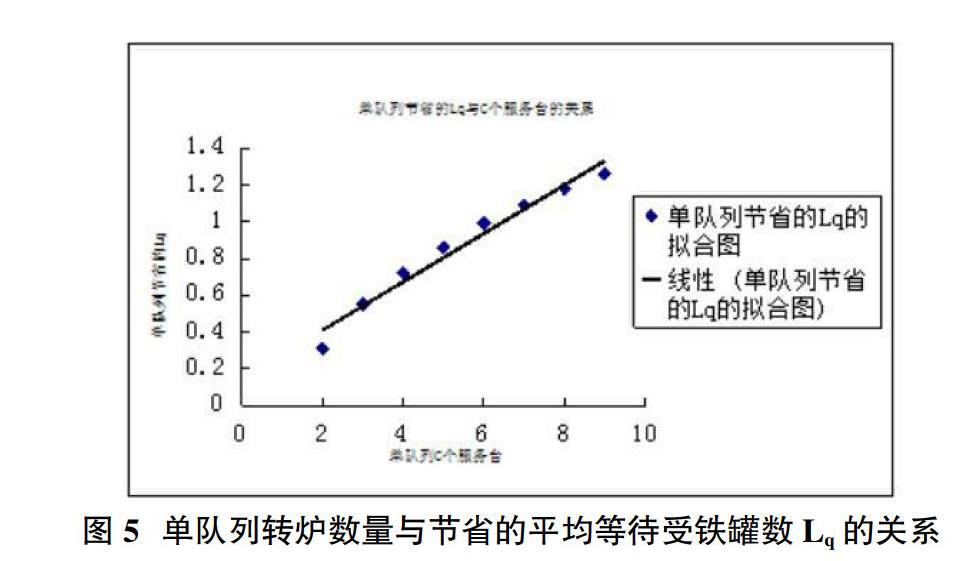
2.4 单队列排队系统下转炉数量对节省的平均等待受铁罐数Lq的影响
单队列排队模式下,转炉数量与节省的平均等待受铁罐数Lq的关系见图5。单队列排队模式下,随着转炉数量的增多,节省的平均等待受铁罐数也越来越多,平均节省了0.87罐。
2.5 单队列排队系统下转炉数量对节省的受铁罐平均等待兑铁时间Wq的影响
单队列排队模式下,转炉数量与受铁罐平均等待兑铁时间Wq的关系见图6。单队列排队模式下,随着转炉数量的增多,节省的受铁罐平均等待兑铁的时间Wq也越来越短;并且对于多队列,随着转炉数量的增多,平均节省了0.633h。
综上所述,通过单多队列中转炉数量对平均等待队长(包括节省的)和平均等待时间(包括节省的)的影响,受铁罐单队列多转炉的排队模型的各项数量指标(平均等待的受铁罐数Lq、进入车轨的平均受铁罐数Ls、受铁罐在车轨内的平均逗留时间Ws和平均等待服务时间Wq等)明显优于受铁罐多队列多转炉的排队模型。
3 结论
通过对钢铁企业受铁罐转炉兑铁作业环节的物流分析,构建其单多队列排队系统;在单多队列排队模式下,对转炉数量对平均等待受铁罐数(包括节省的)和受铁罐平均等待时间(包括节省的)的影响进行讨论,并得到以下结果:
①在数学解析方法(排队论)的基础上,通过实际钢铁企业中的受铁罐转炉兑铁作业,对单队列(M/M/2)和多队列(2个M/M/1)排队系统的主要数量指标进行分析,可发现单队列排队的排队系统的各项数量指标都比多队列排队系统优。
②随着转炉数量的增多,单队列排队方式时平均等待受铁罐数和受铁罐平均等待服务时间得到了优化,节省的也越来越多,其分别平均节省了0.87罐和平均节省了0.633h。从而可为钢铁企业带来直接的经济和社会效益。
参考文献:
[1]孙荣恒,李建平.排队论基础 [M].北京:科学出版社,2002.
[2]唐加山.排队论及其应用[M].北京:科学出版社,2016.
[3]李亚军.钢铁企业高炉——转炉区段界面铁水温降研究[D].沈阳:东北大学硕士论文,2008.
[4]陆风山.排队论及其应用[M].长沙:湖南科学技术出版社,1984.

