UPFC接入对电力系统运行可靠性的影响分析

刘家兵 李晓芳 张旭亮 赵宝 李从飞

（1.云南电网有限责任公司红河供电局 云南省蒙自市 661100 2.南京弘毅电气自动化有限公司 江苏省南京市 210039）

统一潮流控制器（Unified Power Flow Controller,UPFC）是目前最先进的灵活交流输电系统（Flexible AC Transmission System,FACTS）设备之一[1]，它通过控制规律的改变分别或同时实现并联补偿、串联补偿、移相和端电压调整，为电网灵活可靠地控制提供了通用手段，可见，UPFC 设备的接入将会对电力系统的运行可靠性产生较大影响[2-4]。

为了研究UPFC接入对电力系统运行影响，首先需要建立UPFC 的数学模型。文献[5]采用电压源等效模型得到了 UPFC 注入功率表达式；文献[6]基于功率注入法建立了UPFC 的稳态潮流计算模型，研究了UPFC 对系统输电能力的影响；文献[7]对潮流模型对电网运行可靠性的影响进行了比较分析。此外，迄今为止UPFC元件仍然是一种昂贵的电力电子设备，确定其在发输电系统中的安装位置和安装容量是UPFC 实际工程应用中首先要解决的问题，为此，许多研究人员在UPFC 设备的优化配置方面开展了大量研究：文献[8]采用发电成本最低作为优化的目标函数，基于直流潮流模型和 Big-M 法提出了一种对UPFC 在线路中的安装位置和容量进行寻优的算法；文献[9]针对电网局部解环后潮流分布不均的问题，建立了UPFC 多目标优化配置模型，确定了UPFC 在电网中的最优安装位置、运行容量和安装容量；文献[10]利用含UPFC 的负荷削减模型中拉格朗日乘子的物理意义，提出了基于灵敏度分析确定UPFC最佳安装位置的方法。综上所述，现有文献从UPFC 数学模型和优化配置方面开展了较多研究，但是较少文献在可靠性的角度研究UPFC 接入对系统运行的影响。为此，本文通过研究UPFC 的稳态模型，建立含UPFC 的系统状态后果分析模型，提出了含UPFC 的系统可靠性分析算法。并以修改后的RBTS 可靠性测试系统为例，验证了本文UPFC 建模方法和系统可靠性分析算法的正确性，并进一步研究了UPFC 接入地点、负荷水平等因素对含UPFC 的系统可靠性分析的影响。

1 UPFC工作原理和数学模型

UPFC 的结构原理图如图1所示[9]，它由两个共用直流侧电容的电压源换流器组成，并通过两台耦合变压器接入系统。VSC1 通过变压器Tsh 并联接入系统，用来提供或吸收换流器 VSC2 所需的有功功率，同时还能吸收或产生可控的无功功率，为系统提供无功补偿；VSC2 通过变压器Tse 串联接入输电线路，提供一个幅值和相角均可控的电压相量Vse，实现与输电线路间有功和无功的交换，从而控制线路上的潮流。其中，Vse 的幅值和相角变化范围受交流输电系统的电压水平、装置容量和线路输送容量限制，Vs 的幅值和相角的变化范围分布为[0,Vsemax]和[0,2π]。

UPFC 通过控制线路间的电压和相角来控制线路的有功功率传输，在线路ij 上安装UPFC 时可以把UPFC 等效为一个电压控制变量Upq 和一个相角控制变量δ，UPFC 通过提供Upq 和δ 来改变线路的有功潮流分布和线路阻抗[7,11,12]，含UPFC 的输电线路直流潮流模型如图2所示。

图1：UPFC 的基本结构

图2：含UPFC 的输电线路直流潮流模型

线路ij 上的功率可近似表达为[7]：

等效注入功率为：

线路等效阻抗为：

其中，Upq 和δ 分别是UPFC 的电压控制变量和相角控制变量，Pij 是线路ij 的有功功率，θi 和θj 分别是节点i、j 处的相位，△P是等效注入功率，节点Xij 是未安装UPFC 时的阻抗，Xnewij 是安装UPFC 后的等效阻抗。

2 计及UPFC的负荷削减优化模型

在传统的发输电系统可靠性评估中，基于直流潮流的最优负荷削减线性规划模型得到了广泛的使用[13]。当UPFC 设备接入电力系统时，基于直流潮流的线性规划模型转变成为一个非线性化的问题，含有UPFC 的非线性的负荷削减优化模型如下[7]：

图3：UPFC 可靠性评估流程图

图4：MMRBTS 系统接线图

其中式（4）为直流潮流下的最优负荷削减模型的目标函数，也即最优负荷削减量。式（5）-（11）为约束条件，（5）式为节点有功平衡方程式，（6）式为线路潮流计算式，（7）式为发电机组有功约束，（8）式为负荷削减量约束，（9）式为线路潮流约束，（10）式为UPFC 元件电压幅值约束，（11）为UPFC 元件电压相角约束。

图5：UPFC 安装位置对LOLP 指标的影响

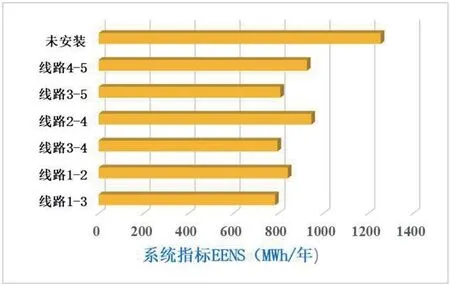
图6：UPFC 安装位置对EENS 指标的影响

图7：UPFC 安装位置对EENS 指标的影响

3 含UPFC的电力系统可靠性评估算法流程

含UPFC 的电力系统可靠性评估算法流程图如图3所示，具体步骤如下：

（1）读入系统参数（各节点参数、线路参数、发电机参数等）；

（2）抽样次数记为0；

（3）抽样次数加1；

（4）用非序贯蒙特卡洛模拟法抽取系统状态；

（5）判断该状态是否已经抽取并评估过，若评估过，则累计相同系统状态的次数。若没有评估过，则进入下一步；

（6）判断该状态下系统是否发生解列，在这里为了简化程序，若系统判断为解列，则不再进行优化。若解列，则进入下一步；

表1：MMRBTS 系统可靠性指标

（7）判断在发生故障情况下，系统各节点出力是否能保持不变，若无法保持不变，则进行优化调度即负荷削减，以使系统恢复原先的安全状态；

（8）若节点出力能够保持不变，计算故障情况下的各线路潮流；

（9）判断线路故障是否导致线路越限，若越限，则进行优化调度；

（10）统计本次系统状态下切除负荷总量，更新指标；

（11）判断是否抽样结束，若没有结束，转步骤3。若抽样结束，则进入下一步；

（12）统计系统可靠性指标。

4 算例分析

本文算例分析中，设置UPFC 的电压控制参数Upq 的范围是[-0.5,0.5]，相角控制参数δ 的范围是[0,2π]。为了验证UPFC 接入对系统运行可靠性的影响，本文首先对经典的RBTS 可靠性测试系统[14]进行了改造，改造方法如下[12,15]：

（1）将原RBTS 系统各个节点负荷扩大为原来的1.3 倍；

（2）在原RBTS 系统的节点1 处增加1 台20MW 的机组，机组参数与原 RBTS 系统节点 2 处20MW 机组相同；

（3）在原RBTS 系统的节点2 处增加2 台20MW 的机组，机组参数与原 RBTS 系统节点 1 处 20MW 机组相同；

（4）在节点5 和6 之间增加线路10，线路10 的参数与线路9相同。

改造得到的MMRBTS 系统接线图如图4所示。

4.1 UPFC安装之前和之后的MMRBTS系统可靠性指标比较

表1 给出了不安装UPFC 时MMRBTS 原始系统和在线路1-3的节点1 侧安装UPFC 元件后的系统可靠性指标，其中LOLP(Loss of Load Probability )为系统失负荷概率；EENS（Expected Energy Not Supplied）为系统缺电量不足期望，单位为MWh/年。由表1可见，安装UPFC 之后，系统的可靠性指标得到了较大的改善。

4.2 UPFC安装位置的影响

图5 和图6 分别给出了UPFC 安装在不同位置时的MMRBTS系统的LOLP 和EENS 指标，由此可见，UPFC 的接入地点对系统可靠性指标的影响较大。对于MMRTS 系统，当UPFC 在线路1-3处接入时，对系统可靠性的改善效果最好。

4.3 负荷灵敏度分析

图7 给出了MMRBTS 原始系统和UPFC 元件安装在1-3 线路两种情况下，不同系统负荷水平时的系统EENS 可靠性指标的变化情况。由图7 可见，随着系统负荷的增加，安装UPFC 后的系统可靠性指标改善效果越显著，这是因为当系统负荷水平增加时，输电系统的容量裕度较小，因此装设UPFC 能得到更加显著的效果。

5 结论

本文研究了UPFC 的基本结构和工作原理，基于直流潮流模型的UPFC 数学模型建立了包含UPFC 的系统负荷削减模型，并提出了考虑UPFC 接入的电力系统可靠性评估算法。最后以MMRBTS系统为例进行了算例分析，算例结果证明了论文所采用的负荷削减模型和含UPFC 的可靠性评估算法的正确性，算例结果表明UPFC设备的接入将会对电力系统的运行可靠性带来积极的影响，本文研究工作能够为UPFC 的接入和考虑UPFC 接入的电力系统规划设计提供参考。