拓扑结构时变的耦合时滞复杂网络自适应同步
邰亚丽 马益聪
(1.集美大学诚毅学院 福建省厦门市 361021 2.集美大学理学院 福建省厦门市 361021)
近年来,随着信息技术的发展,复杂网络的研究成为了许多学科研究的热点。[1-2]在复杂网络的研究中,同步现象广泛存在,对网络同步的研究备受学者关注。[3-4]由于传输速度的有限性、信道的拥堵导致时滞现象广泛存在,在研究复杂网络的同步问题时节点时滞和耦合时滞很有必要考虑。[5-10]由于实际问题中外界的干扰,导致复杂网络的拓扑结构会随时间发生变化,所以在复杂网络中引入时变拓扑结构的设定是有必要的。而且拓扑结构时变的复杂网络要达到同步仅靠自身调节很难实现,所以这类复杂网络的同步问题更加值得学者们研究。[11-14]
本文讨论了一类复杂网络的同步控制问题,这类网络是由相同节点构成,不仅拓扑结构具有时变性而且带有时变时滞耦合项。通过设计一个自适应控制器,实现了这类复杂网络与其孤立节点的同步。最后利用Matlab 数值仿真,验证了该控制器的的有效性和这类网络的可控性。
1 系统描述与预备知识
考虑一个由N 个相同节点构成的复杂网络,网络具有时变拓扑结构且带有时变时滞耦合:
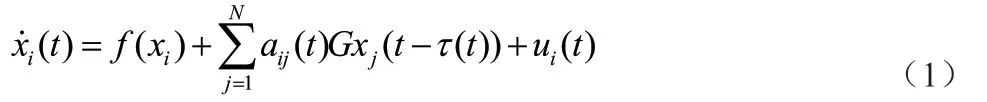
注1:A(t)不一定是对称阵。
假设1[15]向量函数满足Lipschitz 条件,即对于任意的存在正常数l,满足
引理1[16]对任何向量都有不等式成立。
2 复杂网络同步分析与实现
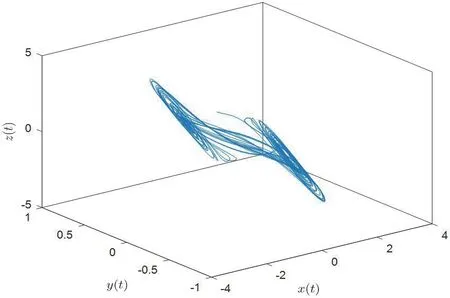
图1:Chua 混沌电路

图2:无控制作用时同步误差
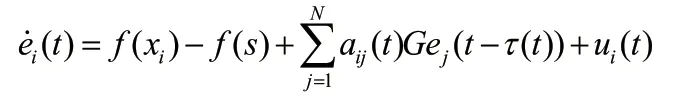
证明:构造Lyapunov 函数:
●基金项目:福建省中青年教师教育科研项目(JT180871)。
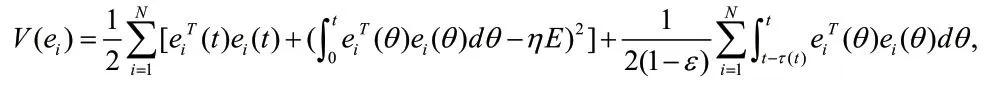
将V(ei)沿误差系统求导,
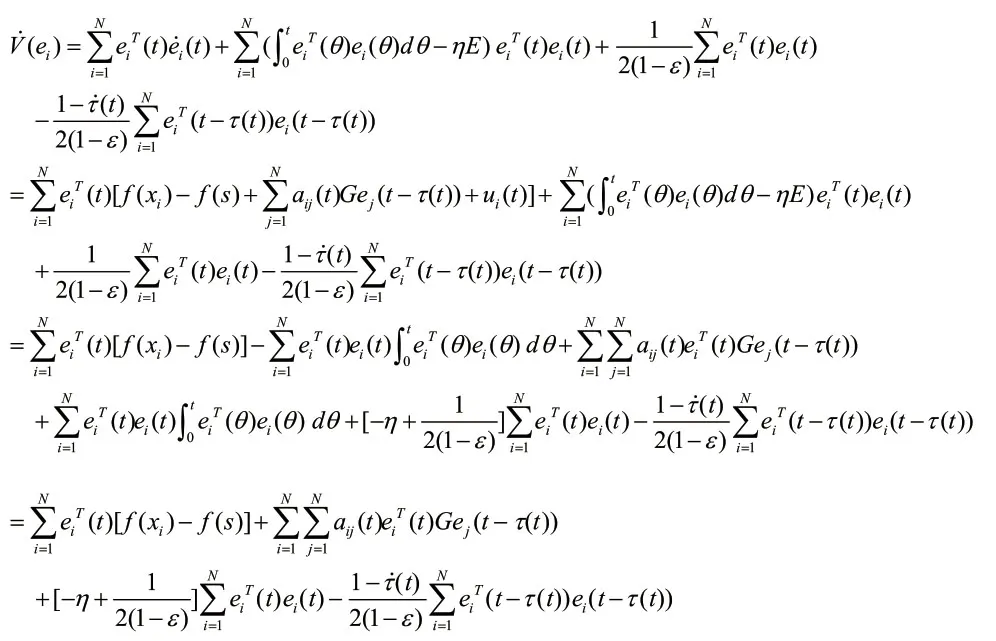

这里的表示PTP 的最大特征值,利用Lyapunov 稳定性理论[17]知,ei(t)渐近地趋于稳定的零解,即复杂网络(1)和其孤立节点s(t)实现同步。
3 数值仿真
例:假设复杂网络的节点个数N=3,选取Chua 混沌电路作为复杂网络(1)的节点状态,状态方程为

复杂网络的状态方程可写为
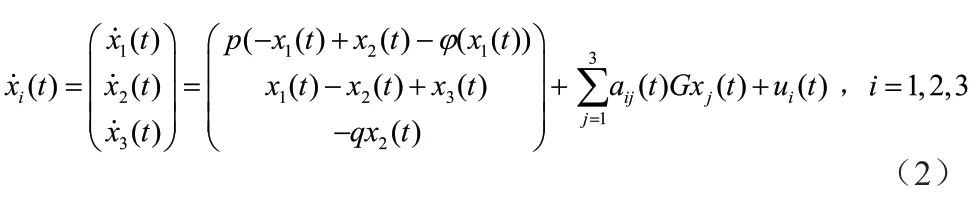
其中外部耦合矩阵为

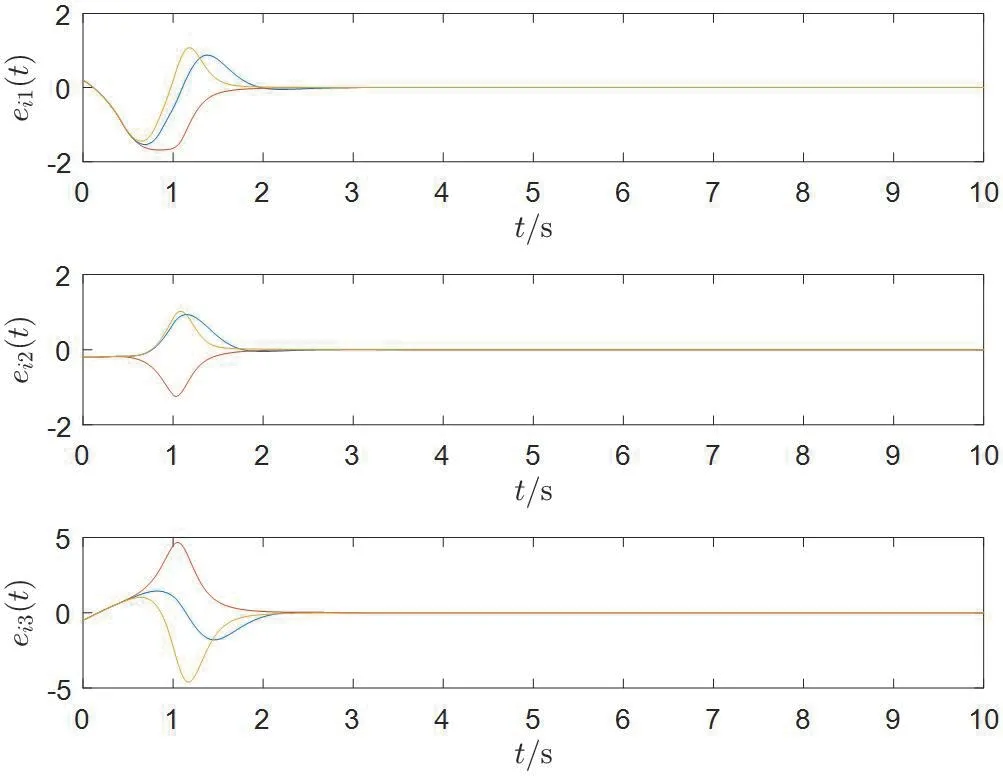
图3:控制器作用下同步误差误差
内部耦合矩阵为

图3给出了给复杂网络(2)施加定理1 中的自适应控制器后的同步误差的演化曲线,可以看出系统在施加了自适应控制器时网络的各节点与孤立节点实现了同步。
4 结论
本文研究了拓扑结构时变且有时变时滞耦合的复杂网络的同步问题。构造Lyapunov 函数并利用稳定性理论经证明得到所研究网络同步的充分条件。最后利用 Matlab 仿真,证实了方法的有效性,如图3所示的网络系统误差快速的趋于0,即说明了网络在施加了本文的自适应控制器后快速地实现了同步。

