数字全息深度学习重建方法
王帅,陈波
(华北理工大学电气工程学院,唐山063210)
0 引言
数字全息技术[1]凭借着无损伤、非接触、高分辨率、实时性以及处理迅速等优点,被广泛应用于形貌形变测量[2]、生物医学细胞成像分析[3]、粒子场测量[4]等领域。数字全息根据记录光路不同可分为同轴全息和离轴全息。同轴全息,在现光波沿同轴方向传播,其光路结构简单,能充分有效的利用了相机的空间带宽。缺点在于直透光、孪生像和原始像不可分离,可以通过多步相移技术[5]有效去除孪生像的干扰,但该方法会导致所谓的两步重建过程,即相位恢复和聚焦,使得重建过程变的复杂。离轴全息图,参考光以一定角度照射探测器,在现时直接将透射光与产生共轭像的衍射光分离,可通过单次曝光采集完成相位测量。而缺点在于,虽然数字全息相位重建技术是利用计算机数字计算完成相位在现,但传统相位重建过程仍多采用人工方法选择实像频谱,限制了重建像质量和重建速度的提高。
近年来,深度学习[6]广泛应用于图像复原[7]、目标分类[8]、图像超分辨率[9-10]等计算机视觉任务中。Yair Riv⁃enson等人用改进的卷积神经网络对使用反向传播算法得到的初步相位图进行全息图像重建[11-12];Ozcan等人提出基于多尺度卷积神经网络的方法用以去除全息重构中的共轭像与零级像,实现了相位恢复和全息图像重建[13];2018年,Ozcan等人提出了基于深度学习的自动聚焦和相位恢复在全息成像中的扩展景深[14];Wonseok Jeon等人利用多尺度卷积网络实现对全息图的去噪处理[15-17];2018年,Wang等人结合Ozcan网络和U-Net网络,提出了一种新型网络结构eHoloNet网络,该网络将同轴数字全息图和原始图像进行端对端映射,然后利用这些特征重建图像[18];2019年,Wang等人提出一种新型的Y-Net网络结构,实现了数字全息重建方法一对二的深度学习框架,可同时重建出单个数字全息图的强度信息以及相位信息[19]。为此本文通过数值仿真方法研究了基于深度学习的全息重建方法。相比于传统的重建方法,经过充分训练的卷积神经网络能一步到位直接重建全息图,无需任何预处理。
1 原理和方法
1.1 数字全息
数字全息术利用CCD等光电探测器记录全息图,即目标光与参考光的干涉信号,然后利用数字信号处理方法模拟光学衍射重构出目标图像。典型的全息光路如图1所示,激光器发出的光束一路通过目标后,携带着目标信息作为目标光,另一路作为参考光,光电探测器记录参考光和目标光的干涉信号:
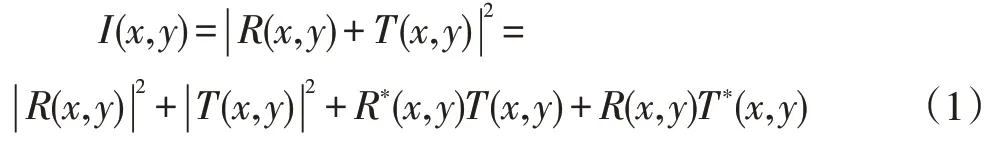
其中R(x,y)和T(x,y)分别表示参考光和目标光在探测平面上的复振幅。
传统的数字全息目标图像重建方法是,采用数字信号处理方法模拟参照光通过全息图I(x,y)的衍射传播,即可得到目标图像。对于离轴全息,通过合理选取目标光和参考光的夹角能够消除孪生像的干扰,但是系统的空间带宽积不能有效利用;对于同轴全息,则需要采用多步相移等方法消除孪生像和背景噪声的干扰。为此,下面重点介绍基于深度学习的目标重建方法。

图1 全息光路图
1.2 深度学习目标重建方法
基于深度学习的目标重建方法核心是构建和训练神经网络模型。神经网络模型经过大量样本的持续训练,最终建立了输入与输出之间的非线性映射关系,即全息图和目标图之间的映射关系,可替代传统算法应用于数字全息图像重建工作。
卷积神经网络能够大幅减少计算量,从而节约计算资源,降低时间成本。因此,使用卷积神经网络来建立我们的网络结构,提出了如图2(a)所示的CNN网络模型,在如图2(a)所示CNN网络结构中主要有三种类型的功能层:卷积层、池化层和全连接层。如图(b)所示为卷积层,它由卷积块和激活函数组成,选用tanh激活函数。为了避免过拟合和梯度消失,我们在网络模型中添加批量归一化(BN)操作和值为0.5的神经节点丢失率(Dropout),以达到增加训练速度和提高网络泛化能力的目的。将全息图以及对应的原强度图输入到网络对网络模型进行训练,训练过程中不断调整网络的超参数,对原有网络进行优化,从而得到更好的输出结果。该网络使用Tensorflow搭建深度学习框架,实现了CNN网络模型。该模型训练的硬件平台为Intel i5-8300H,8GB RAM,NVIDIA GeForce GTX 1050Ti GPU的工作站,软件为Windows10操作系统,Python3.0的编译环境。
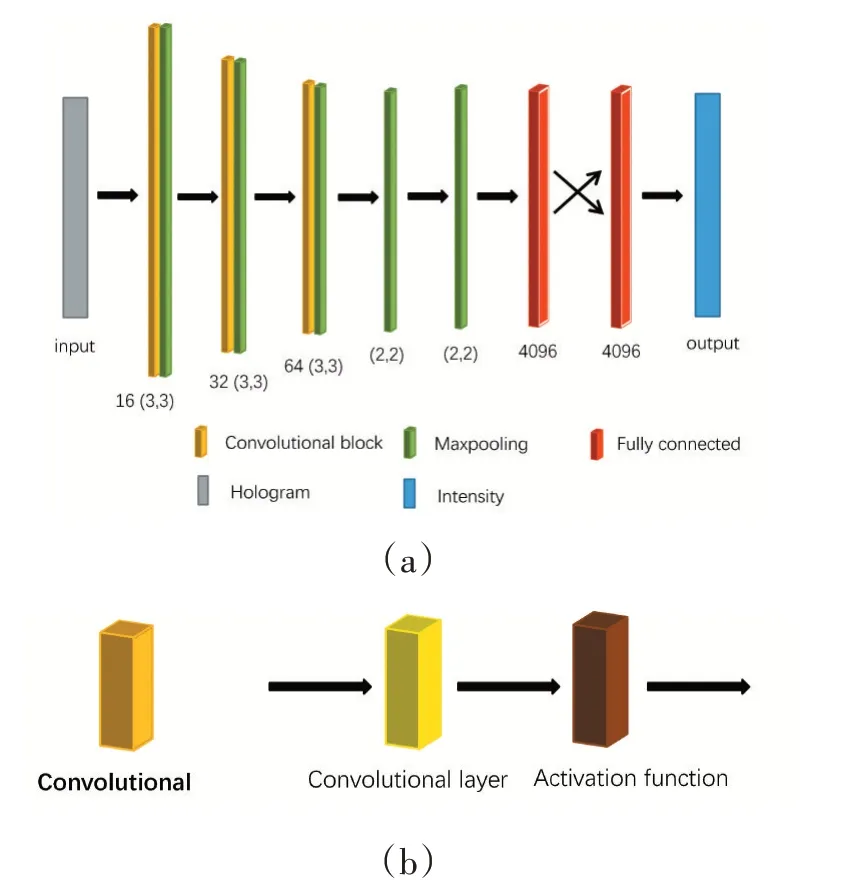
图2 CNN网络模型
利用MATLAB数值仿真获得全息图和对应的原强度图构建数据集,将全息图像作为网络输入,对应的原强度图作为网咯输出。数据集分为训练集和测试集两部分,训练CNN网络过程中,网络只会学习训练集的内容,测试集用于对网络的测试不参与训练过程,当网络模型训练完成后,用测试集测试网络效果,输入测试集内的全息图,CNN模型会迅速输出对应的重建图像。
2 实验和结果分析
2.1 实验模型
在MATLAB中建立了离轴数字全息仿真模型,目标图像大小为64×64像素,通过全息仿真模型得到对应目标的全息图像,图像大小为128×128像素。
利用卷积神经网络来搭建网络结构,如图2所示。将全息图输入网络模型,首先通过三个不同数量过滤器的卷积层(过滤器个数分别为16、32、64),它是由(3,3)大小的卷积核以及tanh激活函数组成,卷积核的移动步幅为(1,1)大小,用来提取图像特征。每一卷积层之后都需要加上相同的池化层,池化步幅为(2,2)大小,并选用的是最大池化方法(Maxpooling)。在这之后,在分别经过两个相同的池化层,通过池化来降低卷积层输出的特征向量,同时改善输出结果,防止过拟合。最后通过两个全连接层(FC),使用两组4096个神经元做全连接,神经元通过激活函数进行输出。激活函数的作用是加入非线性因素,从而解决非线性函数拟合问题,在卷积神经网络模型建立过程中,对比了sigmoid函数、tanh函数、Relu函数等常用的激活函数对损失函数的影响,选择tanh函数作为输入层和隐含层的激活函数。通过全连接层将前面经过多次卷积后高度抽象化的图像特征进行整合,最终输出重建结果。
我们通过数字全息仿真模型进行数据采集。共采集到全息图与相对应的实际目标强度图各8200张,将采集到的数据图像分两类,一类作为卷积神经网络的训练集用于网络模型的特征学习,共8000张;一类作为卷积神经网络的测试集用于对训练好的网络的测试,共200张。数据集中的全息图,图像尺寸大小为128×128像素,如图3所示。利用全息图所对应的原图的强度信息制作标签图像,图像尺寸大小为64×64像素,对应的标签图像如图4所示。

图3 全息实验图像

图4 标签图像
我们将损失函数定义为均方误差(MSE),并对网络超参数进行一定的设置,具体网络模型训练超参数如表1所示。
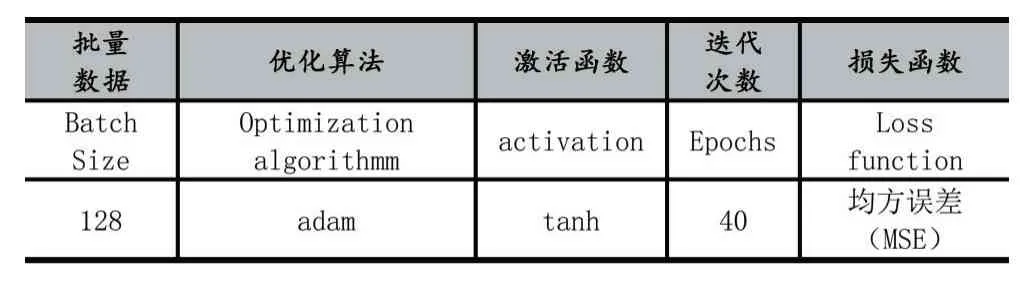
表1 卷积网络模型训练参数
2.2 实验结果
应用表1中的超参数对网络进行训练,我们采用MSEloss(均方误差)作为训练过程中的损失函数,训练结果如图5所示。图5绘制了相对应的train-MSEloss和test-MSEloss随循环迭代次数(epoch)的loss曲线。循环迭代次数为40次,最终稳定在0.0017左右,训练完毕。
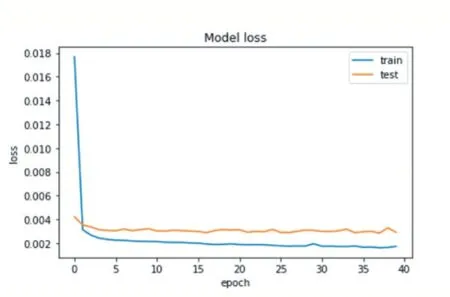
图5 网络模型loss曲线
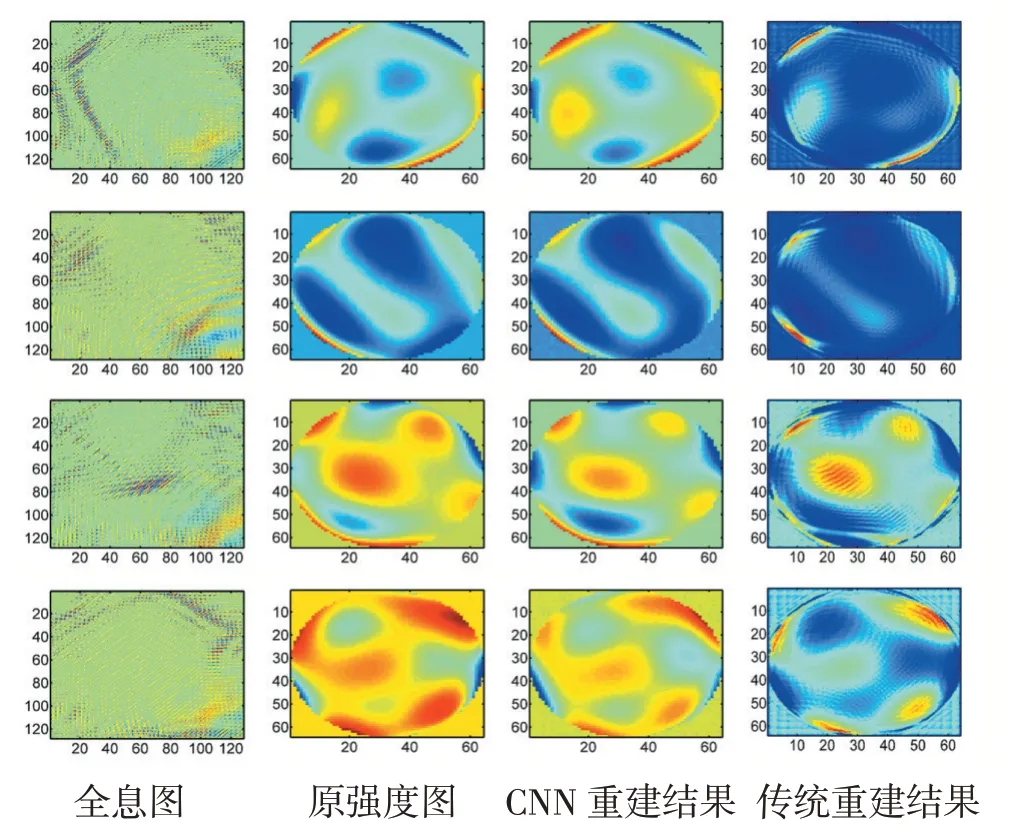
图6 重建测试结果
从测试集中随机选择4组全息重建结果进行误差分析,如图6所示。第一列为实验平台采集的全息图像,我们采用均方根的方法进行误差对比,通过计算第二列原强度图和对应的第三列CNN重建图的均方根,来反映重建结果的好坏,得到4组重建误差的均方根值分别为:0.0435、0.0299、0.0411、0.0537,结果说明基于深度学习的全息重建方法具有较高的重建精度,能够端对端的一步到位而无需任何预处理,直接利用全息图重建出物体的强度信息。
为了更直观体现CNN网络模型对单幅全息图的重建效果,选用了经典传统傅里叶变换全息重建方法来进行对比分析,重建结果如图6第4列所示。从图中通过CNN重建结果与传统重建结果对比可以看出,卷积神经网络重建结果优于传统重建结果,极大提高了重建效率,并且无需反向传播处理,简化了全息重建过程。
3 结语
在这篇文章里,我们提出一种新的CNN网络结构,即一种数字全息深度学重建方法,该方法大大减少了实验所需数据量,使得数字全息重建效率显著提升。该模型通过建立端对端的映射关系,学习图像特征,实现全息重建,克服了传统数字全息重建过程中孪生项、直流项的影响。通过使用CNN网络模型,可以直接重建出物体的强度信息,并且重建是一个一步完成的过程,无需反向传播。

