基于非对称弯曲理论的预制箱梁单梁静载试验应力研究

梁茜雪

摘要：针对非对称预制预应力箱梁静载试验中实测应力与理论计算偏差较大的现象，文章通过对非对称预制箱梁试验应力影响因素以及常规对称弯曲理论应力计算局限性的分析，提出了基于非对称弯曲理论的预制箱梁应力计算方法。计算实例表明，该方法计算的各测点应力与实体模型计算结果相对偏差仅为-0.37%～2.92%;约束扭转引起的纵向正应力在常规混凝土截面箱梁影响较小，小于总应力的1%;非对称预制箱梁试验时的纵向弯曲变形属于非对称弯曲，中性轴与水平轴呈一定夹角。

关键词：箱梁;单梁试验;应力;非对称弯曲;约束扭转

0 引言

预应力预制装配式混凝土结构因具有工厂集成化的优势，可有效提高施工质量和效率，广泛应用于我国公路桥梁施工中[1-4]。目前的中小跨径公路桥梁上构多为简支梁和连续梁，主梁采用预制装配式预应力混凝土梁，常见主梁截面形式为空心板、箱梁和T梁等。在架设梁板之前，需要通过单梁静载试验确保施工质量满足规范及设计要求，而现有规范对单梁静载试验的规定不明确，与非对称弯曲的预制箱梁结构应力计算相关的研究也不多[5-8]。本文主要以实际工程中发现的不符合现象为研究出发点，对非对称预制箱梁单梁静载试验中的应力不对称现象进行研究。

1 对称弯曲理论在单梁静载试验中的研究现状

1.1 单梁静载试验方法

单梁静载试验时结构形式属简支梁，因此传力简单、受力特征明确、影响因素少，根据试验结果进行承载能力判断的可靠性很高。试验属于构件试验，可在试验室、预制场或已架设的桥梁上实施。试验对象为预制单梁（也称裸梁），加载方式主要有千斤顶配合反力架加载和重物加载两类。试验前按施工顺序及对应的结构体系建立成桥计算模型，分析主梁在恒载和设计活载作用下的荷载效应，扣除预制梁自重后，依据应力等效原理得出试验状态下裸梁的荷载效应，再反算出试验荷载值。试验时在裸梁上分级施加试验荷载，测量各测试截面的应力（应变）和挠度等响应，观察裂缝扩展情况，通过实测响应与计算值比较分析判断预制梁的强度、刚度和受力状况是否达到设计要求。单梁静载试验时弯矩测试截面一般布置于简支梁四分点处，应变测点分别对称布置于腹板和底板，测量横截面上的沿梁纵向应变，挠度测点对称布置于底板。测点布置见图1。

1.2 对称弯曲理论及局限性

当梁横截面有对称轴且梁上所有横向力或（及）力偶均作用于包含该对称轴的纵向平面上时，梁变形后的轴线是纵向对称面上的平面曲线，这种变形称为对称弯曲[9]。根据对称弯曲理论，弯曲时横截面绕通过形心且垂直于纵向对称面的轴，即中性轴旋转。在各纵向纤维间互相不挤压、拉伸和压缩时弹性模量相等条件下推导出对称弯曲时横截面上正应力计算式[9]：

为与整体式现浇箱梁区别，预制装配式混凝土箱梁常被称为“小箱梁”，其较空心板和T梁有抗扭能力强的优势，故成桥时横向刚度较好，是使用较多的预制梁截面。预制箱梁的中梁截面一般按纵向对称设计。因功能需要，边梁外翼缘多较内翼缘长，所以边梁常规截面为非对称截面，无纵向对称面。

单梁试验的受力分析常采用梁单元建立有限元模型，计算出各级试验荷载下试验梁的应力和挠度。空间梁单元一般有六个自由度，变形模式包括轴向拉伸、2个主平面内弯曲以及扭转变形的组合。其中纵向弯曲正应力按对称弯曲理论计算，认为挠曲线位于横向力与纵轴平面内，截面绕通过形心且与横向力垂直的坐标轴转动。单梁试验时的荷载均为竖向荷载，在计算模型中，梁单元截面绕水平轴发生平面转动，故应力沿梁高呈线性变化，即同一梁高处的应力相同。但在实际试验时，边箱梁经常出现同一截面两侧相同高度实测应变差异较大的现象，其中腹板较底板明显，最大相差约50%。试验现场对可能造成影响的支座安装偏差、加载偏位、布点质量、仪器故障等因素进行了逐一排查，未發现异常，认为试验数据真实可信。表1选取两片边箱梁单梁静载试验应变结果以说明应变分布规律。

2 非对称弯曲应力计算

为避免加载时试验箱梁发生侧倾，试验荷载的横向位置应对称于支承中线布置，即对称于底板中心线。非对称箱梁的截面形心不在底板中心线处，故试验荷载合力作用线偏离形心，属于偏心荷载。箱梁在偏心荷载作用下，将产生纵向弯曲、扭转、畸变及横向弯曲四种变形[10]。其中试验荷载在顶板直接受荷部分产生横向弯曲，同时引起其他部分的横向弯曲，从而在纵截面上产生正应力及相应的剪应力。但单梁试验关注的是试验梁在横截面上的承载力，所以测试应变为横截面上正应力，故在研究单梁试验应力时无须考虑横向弯曲变形的影响。另由于混凝土箱梁截面尺寸均较厚，且端部和中部多布置横隔板，畸变引起的应力很小，可不计入。综上，研究非对称预制箱梁在单梁静载试验时应力可忽略横向弯曲和畸变，仅通过分析纵向弯曲和扭转变形对应力的贡献来获取满足试验分析要求的精确计算应力。

2.1 纵向弯曲正应力分析

非对称预制箱梁无纵向对称面，在试验荷载作用下的弯曲变形不再遵循对称弯曲理论的规律，变形后轴线不在某个平面内，截面转动的方向与弯矩向量及截面特性有关。非对称截面梁的弯曲变形均为非对称弯曲，弯曲时横截面仍符合平面假定，中性轴通过形心，方向由弯矩确定。

作用在梁任一横截面上的弯矩M可分解为通过任意一对相互垂直的形心轴上的两个分量My和Mz，依据非对称弯曲理论的广义弯曲正应力公式为[10]：

在确定测试截面竖向平面内的弯矩后，根据截面特性和测点与形心相对位置由式（4）可计算出各测点应力值，由式（5）计算中性轴的方向。

2.2 约束扭转正应力分析

非等直圆杆在扭转时横截面不再保持平面，除转动外还发生翘曲。当纵向纤维未受到约束时，横截面上仅有扭转剪应力τk，此时的扭转为自由扭转;当纵向纤维受到约束后，除扭转剪应力τk外，还产生翘曲正应力σω以及由翘曲正应力σω引起的约束扭转剪应力τω[10]。箱梁在静载试验时的扭转变形属约束扭转，所以需分析与试验应力有关的翘曲正应力σω。

约束扭转的翘曲正应力σω采用基于乌曼斯基闭口截面薄壁杆件理论的薄壁效应算法按式（6）计算[11]：

目前的有限元结构分析软件，如ANSYS、Midas Civil等已增加了七自由度梁单元，即在原六自由度基础上增加了约束扭转双力矩作为第七个自由度，可计算箱梁截面的约束扭转效应，包括约束扭转剪应力和翘曲正应力。虽然采用七自由度梁单元建模分析可计算出弯曲正应力和约束扭转正应力的组合应力，但弯曲正应力仍依据对称弯曲理论计算，因此软件提供的组合应力不是准确计算应力，需要设法得出单独的约束扭转正应力。

2.3 组合应力计算

根据以上分析，非对称预制混凝土箱梁静载试验纵向应力可表示为纵向弯曲正应力σM和约束扭转正应力σω的组合应力。按非对称弯曲理论和薄壁效应算法编制计算程序，分别计算出纵向弯曲正应力σM和约束扭转正应力σω，由此得到组合应力σ=σM+σω。σω的计算也可采用支持含约束扭转双力矩自由度梁单元的有限元结构分析软件单独计算。在梁单元模型中施加绕梁轴线的力偶，力偶的位置、大小和方向由荷载及偏心位置确定，此时无弯曲变形，横截面上正应力仅包括约束扭转正应力。

3 计算实例

某预应力预装配混凝土箱梁桥，上构形式为4×25 m连续梁，横向布置5片箱梁，预制箱梁高1.5 m、宽2.85 m，混凝土强度等级为C50，设计荷载为公路-Ⅰ级。对1#跨左侧边箱梁进行单梁静载试验，加载方式为预制块加载，每块重7 t。以跨中截面为控制截面，预制块总重56 t，在跨中截面产生弯矩My=2 799 kN·m。应变测点布置见图1，加载布置见图3。选取1片边箱梁进行单梁荷载试验应力分析，分别采用Midas Civil建立六自由度梁单元模型、本文组合应力算法和Midas FEA建立实体单元模型三种方法计算边箱梁在试验荷载下跨中截面纵向正应力。将前两种方法计算出的应力和中性轴位置与实体模型结果进行比较，以分析各方法偏差程度，研究本文算法的可靠性。

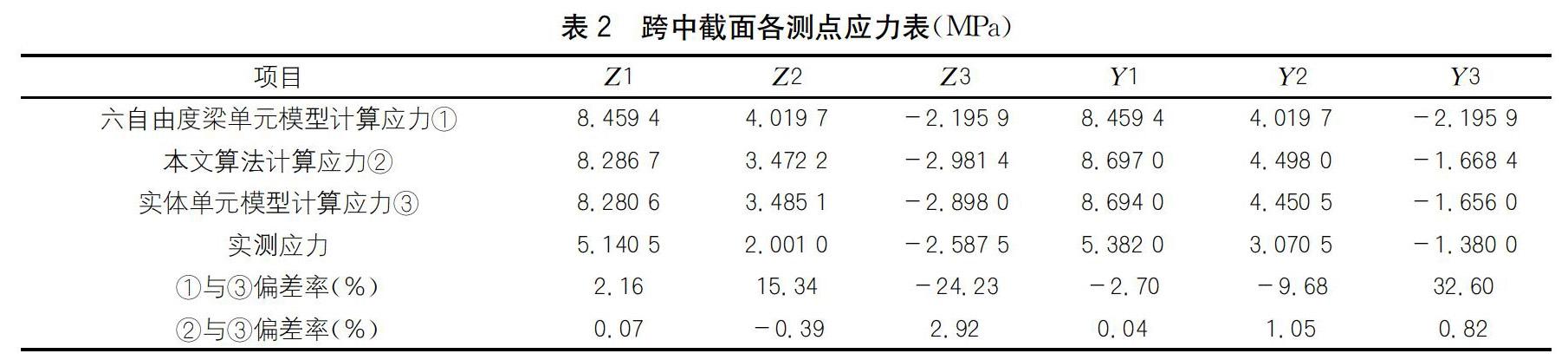
由表2可见，六自由度梁单元是依据对称弯曲梁理论计算截面应力，中性轴的位置为通过形心的水平轴。各测点应力与实体模型计算结果相对偏差为-24.23%～32.60%，与实体模型计算的中性轴距离越近则测点应力相对偏差越大。没有纵向对称面的预制箱梁单梁试验时的变形与对称弯曲变形明显不符，仍采用对称弯曲理论计算弯曲正应力将产生较大误差，直接影响对裸梁承载能力的判断。而按组合应力计算的各测点应力与实体模型计算结果相对偏差仅为-0.37%～2.92%。表4、图4和图5的结果显示中性轴位置与有限元实体模型计算结果高度吻合，说明本文提出的精确算法准确性好、精度可靠，是计算非对称箱梁和其他非对称截面梁结构应力计算的实用方法（见表3）。

表3分别列出了弯曲正应力σM和约束扭转正应力σω的结果，组合应力中σω未达到总应力的1%，对纵向应力的影响很小。约束扭转引起的纵向正应力在常规混凝土截面箱梁影响很小，可不考虑。但对大型箱梁截面和箱壁较薄时应利用薄壁结构理论分析约束扭转应力的影响，避免产生较大误差。

非对称预制箱梁单梁试验时的纵向弯曲变形属非对称弯曲，梁截面变形仍符合平面假定，但中性轴为与水平轴呈一定夹角的斜轴。本算例按组合应力计算的中性轴与Y轴的夹角θ=90.025 8°，中性轴与水平方向夹角仅为0.025 8°，但两侧应力分布差异明显。因此非对称箱梁的两侧应变测点应根据中性轴的位置调整，避开接近零值位置，无须再按对称布置。

4 结语

通过对非对称预制箱梁在单梁试验时纵向正应力主要变形的研究，推导出单梁静载试验时的纵向弯曲正应力和中性轴夹角公式。研究过程中得到了一些有益的结论：

（1）没有纵向对称面的预制箱梁单梁试验时的变形与对称彎曲变形明显不符，采用常规对称弯曲理论进行箱梁应力计算分析误差较大。

（2）本文方法计算出的各测点应力与实体模型计算结果相对偏差仅为-0.37%～2.92%，在非对称箱梁和其他非对称截面梁结构应力计算方面优势明显。

（3）约束扭转引起的纵向正应力在常规混凝土截面箱梁影响较小，小于总应力的1%，试验过程中可不考虑该因素的影响。

（4）非对称预制箱梁单梁试验时的纵向弯曲变形属非对称弯曲，梁截面变形仍符合平面假定，但中性轴为与水平轴呈一定夹角。

参考文献：

[1]陈卓异，黄 侨，李传习，等.波形钢腹板组合槽型梁静载试验与有效预应力分析[J].土木工程学报，2018，51（8）：60-70.

[2]刘邵平，姜 燕.城市轨道交通U型梁静载弯曲试验加载方案研究[J].南京工程学院学报（自然科学版），2016，14（2）：79-82.

[3]关良勇，黄应征，张永平.30 m预应力混凝土T梁单梁静载试验[J].公路交通科技，2018，167（11）：155-157.

[4]毕硕松.单梁动静载试验快速检测技术研究[D].西安：长安大学，2013.

[5]肖宏笛，史晓贞.基于静载试验的公路桥梁预制单梁板承载能力评定[J].中华建设，2018（7）：148-150.

[6]吴 捷.索形优化后的双向张弦梁静载试验分析之全跨均布荷载下的上弦钢梁[J].清华大学学报（自然科学版），2014，54（11）：1 396-1 406.

[7]刘忠平.预应力型钢混凝土梁静载及疲劳试验研究[J].铁道建筑，2019，59（9）：13-18.

[8]周叶飞，曾明杰.预制小箱梁单梁静载试验及承载能力评定分析[J].中外公路，2015，35（2）：142-146.

[9]孙训芳，方孝淑，关泰来，等.材料力学[M].北京：高等教育出版社，2009.

[10]项海帆.高等桥梁结构理论[M].北京：人民交通出版社，2013.

[11]包世华，周 坚.薄壁杆件结构力学[M].北京：中国建筑工业出版社，1991.