核心素养视野下一道中考压轴题的分析与启示
◎ 成鸣娟
中考数学压轴题综合性强,涉及的知识点多,对不同水平的学生进行区分和选拔,在中考中举足轻重。笔者针对陕西省2017数学中考题25题略谈粗浅认识,不当之处请指正。
一、试题呈现
(2017年陕西数学中考题第25题)
问题提出
1.如图1,△ABC是等边三角形,AB=12。若点O是△ABC的内心,则OA的长为_______。
问题探究
2.如图2,在矩形ABCD中,AB=12,AD=18。如果点P是AD边上一点,且AP=3,那么BC边上是否存在一点Q,使得线段PQ将矩形ABCD的面积平分?若存在,求出PQ的长;若不存在,请说明理由。
问题解决
3.某城市街角有一草坪,草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成,如图3所示。管理员王师傅在M处的水管上安装了一喷灌龙头,以后他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水。于是,他让主喷灌龙头的转角正好等于∠AMB(即每次喷灌时喷灌龙头由MA转到MB,然后再转回,这样往复喷灌),同时,再合理设计好喷灌龙头喷水的射程就可以了。如图3,已测出AB=24m,MB=10m,△ABM的面积为96m2;过弦AB的中点D作DE⊥AB交弧AB于点E,又测得DE=8m。
请根据以上提供的信息,帮助王师傅计算喷灌龙头射程至少多少米时,才能实现他的想法?为什么(结果保留根号或精确到0.01米)?

图1
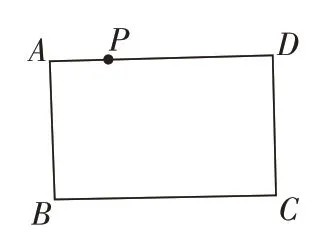
图2
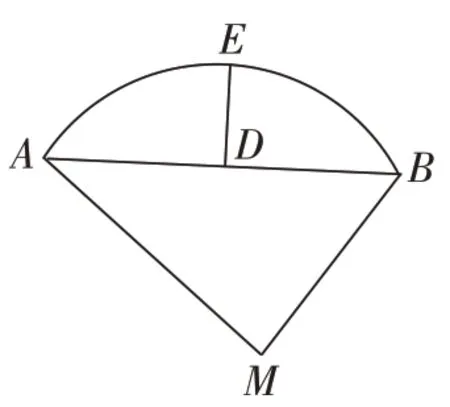
图3
二、解题过程分析
第1 问:考查等边三角形的内心,构造直角三角形,应用勾股定理解得:
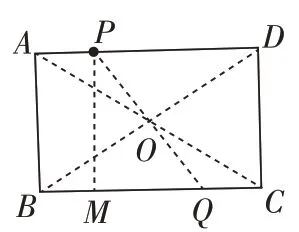
图4
第2问:如图4:
连接AC、BD相交于点O,连接PO并延长交BC于点Q。则线段PQ将矩形ABCD的面积平分。
∵点O为矩形ABCD的对称中心,CQ=AP=3。过点P作PM⊥BC于点
点评:考查平行四边形的中心对称是典型的面积平分问题,以往平分面积是定性分析,而这道题是定量计算,在这一细节上稍提升难度,高于平时练习。
第3问:如图5,作射线ED,
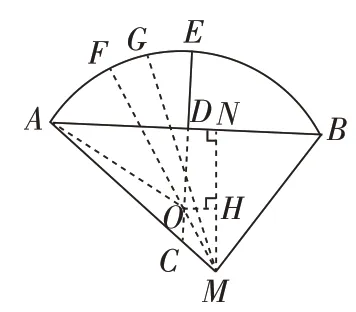
图5
∵AD=BD,ED⊥AB,弧AB为劣弧,∴弧AB所在圆的圆心在射线ED上。
假设圆心为O,半径为r,连接OA,则r2=122+(r-8)2,
解得:r=13,∴OD=5。
过点M作MN⊥AB物N,
∵SΔABM=96,AB=24,∴MN=8,NB=6,AN=18,
∵△ADC~ΔANM,∴
∴O在ΔAMB内部。
连接MO并延长交弧AB于点F,则MF为草坪上的点到M的最大距离。
在弧AB上任取一异于点F的点G,连接GO、GM,
∴MF=FO+OM=GO+OM>GM.
过O作OH⊥MN,垂足为H,则OH=DN=6,MH=3。
∴MF=MO+r=
点评:第3问的基本思路:一找二算。对于如1、2问之后,自然在解法思路上有一些相通之处,提炼出前两问的共同之处,关键的线段都和中心点(内心或对称中心)有关系,于是第3问,联想到利用圆心找最短距离。最短距离是直径的一部分,这样思路就打开了。在最短距离的计算中,前两问共同之处用到了勾股定理,那么第3问能否应用勾股定理解决.如何计算最短距离,圆中计算,基本量就是半径r,如此解题思路便越来越清晰。本题要用到勾股定理、相似三角形、等面积法等知识,综合性强,体现了中考命题原则中的“选拔”。
本题前两问考查基础知识和基本技能,关注不同学生的学习状况。第3问有一定难度,渗透考查数学基本思想:数学抽象、逻辑推理、数学建模,是核心素养中最重要的数学思维品质。在计算最短距离中考查了数学运算、直观想象。
作为压轴题,该题区别于前几年陕西的25题,以往以纯数学知识为载体进行考察,而该题以实际问题为背景,学生首先要能将实际问题转化为数学问题:要能找到“喷灌龙头最短射程就是线段FM的长度”,这是该题的难点,也是题目的创新之处。导向到对数学应用能力和意识的培养上,立意新数学味道浓厚且具生活气息,有较高的区分度。对深化数学课程改革有很好的引领作用,是本次试题的亮点。
三、教学启示
中考数学试题一方面检测学生的学习情况,另一方面指导教师的数学教学。通过分析该题目,笔者对初中数学教学提出以下建议。
1.树立模型意识,提高问题解决能力
本题一改往年陕西25题的纯数学背景,立足民生,以城市街角的草坪灌溉为背景,综合初中数学知识设计问题。考查“从实际问题中抽象出数学模型”的能力,这一导向体现了学习的最终目的,即服务于生活,也是对数学核心素养的落实。
每年中考试题有一部分题目,虽然题型和考查方式较为固定,学生也练习过大量的类型题,但这些题依然丢分,比如三角函数、相似三角形、一次函数等相关的应用题。如果以其他数学知识作为载体设计实际问题,或对常规应用题进行变动,学生的得分率会更低,说明学生解决实际问题能力较弱,问题解决能力需要提高。
中考是初中教学的指挥棒,特别是中考压轴题,一定程度引导着教师的教和学生的学。本题旨在提醒一线数学教育者应适当调整教学比重,不仅要关注纯数学问题的求解,还应注重数学应用,帮助学生树立数学应用意识。在日常教学中,注重引导学生了解数学概念产生的背景,针对每一个知识点,尽可能创造生活情境,引导学生提炼数学知识,整合数学信息,在解决实际问题的教学中提高应用数学的能力,最终提高数学建模能力。
2.渗透数学思想,发展数学核心素养
数学核心素养是保障数学学科育人的关键,是在数学知识技能的学习过程中形成的,是在渗透数学思想中发展的。《普通高中数学课程标准》明确提出了六大核心素养,即数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。数学抽象、逻辑推理、数学建模反映的是数学基本思想,也是最基本的素养。
教师在教学中引导学生反思解题过程,理解和掌握数学思想方法,关注知识的发生和发展过程,注重解题的思路来源,加强变式训练,促进数学思想方法的内化。一题多解,多题归一,引导学生抽象出数学本质,提炼出数学思想。在复习课教学中,设置数学思想专题课,用数学思想统领全局,引导学生体会同一个数学思想在不同知识点、不同方法中是如何渗透的,从而提高学生的数学思维品质,发展数学核心素养,获得良好的数学教育。

