基于三维运动轨迹的高分辨显微CT环状伪影去除方法
李静,郑良,陈璐杰,罗守华
东南大学 生物科学与医学工程学院,江苏 南京 210000
引言
高分辨显微CT可达到微米级别分辨率,能对骨骼、牙齿、生物标本等离体标本进行高分辨的三维成像[1]。为了实现系统的高空间分辨率,高分辨显微CT系统大多采用了X线耦合可见光系统高分辨探测器[2],该探测器的核心部件是将X射线转化为可见光的超薄闪烁体,当系统的成像分辨率达到2 μm时,闪烁体的厚度需要小于10 μm才可在景深范围内确保清晰成像。如此薄的闪烁体,其研制过程中不可避免地会引入损坏或响应不一致的像素点,在圆轨迹重建下,最终的重建图像会出现环状伪影[3]。环状伪影在重建图中的表现为以旋转中心为圆心的同心圆(图1a),在正弦图中为竖直方向的直线(图1b),严重的环状伪影会影响图像的后续处理及量化分析。

图1 环状伪影在高分辨显微CT重建图及正弦图中的表现注:a. 牙签重建图像;b. 相应的正弦图。
目前的环状伪影校正方法主要分为三类:第一类是硬件校正方法[4],其中最为常见的方法是通过移动探测器破坏环状伪影的形成机制,使得探测器像素坏点反投影后的误差分散到重建图像各处,使其无法形成环状;第二类是投影域校正方法[5-6],Münch等[7]提出对投影数据进行离散傅里叶变换或小波变换,Liu等[8]也提出可利用低通滤波器滤除水平方向的高频分量来抑制环状伪影,Sun等[9]通过迭代算法对X射线波谱进行修正从而去除环状伪影等非线性伪影;第三类是重建域校正方法,常用的算法是使用极坐标变换法[10-11]将直角坐标系中的环状伪影映射为极坐标系中的线状伪影,再使用一系列线状伪影去除算法对其进行检测以及校正,再将图像变换到直角坐标系[12-13]。
这些环状伪影抑制方法虽然都能一定程度上能够去除环状伪影,但是也相应地存在一些不足。投影域算法中的低通滤波器法会过滤掉部分有效信号,其次迭代类型算法[14],大都存在运行时间过长、不适用于实际等问题;重建域校正算法里的极坐标变换法由于多次使用插值操作,造成图像分辨率下降;而移动探测器的硬件校正方法图像质量好、重建时间快,不过对硬件精度要求高。图2所示为本实验室自研高分辨显微CT系统,其具有光学放大装置以及X线耦合可见光成像系统(虚线框所示),其中X线耦合可见光成像系统内包含了易引入环状伪影的闪烁晶体。因此移动探测器成本高且非常容易影响图像质量,移动探测器的环状伪影硬件校正方法在高分辨显微CT系统并不适用。

图2 高分辨显微CT实体图
针对以上方法的不足并结合高分辨显微CT系统的结构特点,本文提出了一种基于三维运动轨迹的高分辨显微CT环状伪影去除方法,该方法主要包括两个部分:三维运动轨迹的位移矩阵测量以及结合位移矩阵的FDK重建。位移矩阵测量需要对图像进行配准,我们采用了Insight Segmentation and Registration Toolkit (ITK)平台。ITK是一个开源、跨平台的医学图像处理类库,主要用于医学图像的预处理、分割及配准。基于ITK的配准算法简化了医学图像配准程序的开发工作,为医学图像引导临床诊断的研究应用提供参考,是一种成熟的图像配准平台。为了增强该方法的实用性,本文中选用了FDK算法进行重建。FDK算法是由Feldkamp、Davis和Kress提出的一种基于圆形轨道扫描的锥束CT近似解析重建算法,具有重建速度快、可以局部重建的优点,是一种应用广泛的实用型算法。本文提出的环状伪影去除方法对环状伪影去除效果好、重建速度快,适合于高分辨显微CT系统。
1 算法
1.1 三维运动轨迹去环原理
传统的高分辨显微CT中待测物体的运动轨迹为转台形成的圆轨迹,重建过程中环状伪影的形成机制如图3所示[15]。若单个探测器像素存在响应不一致,此误差值在反投影后会平均分布在探测器像元与射线源焦点的连线上(如图3中线L所示)。高分辨显微CT成像过程中探测器与射线源相对静止,转台围绕着旋转中心旋转采图,这意味着每一个角度的探测器像元与射线源焦点的连线到旋转中心的距离始终保持不变。反投影后的误差数据经圆周累加后会出现图3的所示的情况,伪影较为稀疏的区域会被探测器其他像元测量得到的正确数据修正,而较为密集的区域则在重建图像中切出一个以旋转中心为原点、d为半径的环状伪影。

图3 成环机制
本文中加入了可移动的三维平移台并结合旋转台,在空间中形成全新的三维运动轨迹从而破坏圆轨迹的成环机制。在平移台移动过程中,旋转台、源以及探测器的位置均没有发生改变。图4a~c是平移台移动不同位置的重建图像,移动位置分别为左上,中间,右上。图中可以看出重建图像的旋转中心以及环状伪影的成像位置没有改变,变化的是物体在重建图中的位置。图4d指的是将a~c三张图像针对成像物体进行配准后叠加的结果,图4e是将成像物体去除之后环状伪影误差线的叠加结果,可以看出误差线被分散到了图像的各处,环状伪影的成像机制被破坏了。伪影数据被打乱并分布到重建图像各处。对于某个重建数据点而言在特定角度下获得的是伪影数据,但是在其他角度下得到的是真实数据,该重建数据点的伪影数据被真实数据平均,因此不会出现某个数据点的所有角度都是伪影数据而导致此点的重建值误差异常突出的情况。由上述可知通过平移台移动多位置并完整拍摄n圈图像,将他们配准后叠加可以得到去环的效果。但是此种方法扫描时间长,且每一次重建都要进行配准操作,导致重建过程过于复杂而缺乏足够的实用性。
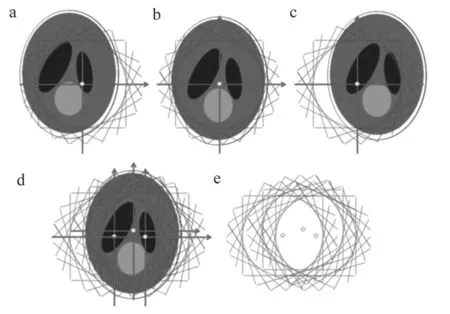
图4 移动平移台去环原理
图5a中将CT的圆周扫描轨迹等角度间隔划分,红点和黄点表示只有旋转台旋转待测物体时产生的圆周轨迹。图5b中是使用三维平移台以及旋转台产生的三维运动轨迹。黑点表示待测物体只有旋转,灰点表示待测物体平移之后旋转,图5b中可以看出物体平移之后旋转中心没有变化但是旋转半径发生改变,因此形成了图中所示的待测物体质心的三维运动轨迹。高分辨显微CT拍摄的一圈投影图中属于不同平移台位置的投影图间错排列,我们将平移台在拍摄过程中需要在不同位置之间不断抖动的采图方式称为单圈抖动拍图,本文中使用了单圈抖动的采图方式来去除环状伪影。

图5 单圈抖动拍图注:a. 圆轨迹;b. 三维运动轨迹。
基于三维运动轨迹的高分辨显微CT环状伪影去除方法具体流程为:首先使用重复定位精度优秀的三维平移台移动到多个固定位置拍摄模体,通过三维图像配准算法进行位移矩阵测量。获得位移矩阵之后,使用单圈抖动来拍摄待测物体。最后,利用本文提出的基于位移矩阵的FDK算法进行重建,达到去除环状伪影的效果,流程图见图6。
1.2 三维亚像素刚性配准算法实现
本文中三维图像的亚像素配准基于ITK实现[16],配准的过程主要包括四个模块:变换模型、插值方式、相似度计算、优化方法选择。由于本文中使用了重复定位精度优秀(0.05% F.S)的三维平移台进行平移台移动,平移过程中待拍摄物体不存在非刚性变换以及旋转,因此配准只需要考虑三维刚性平移变换。此外插值方法是三线性插值,相似度计算为均方误差方程,优化方法选取正则化步长梯度下降法。基于ITK的配准实现伪代码如下所示:① 设置Transform、Interpolator(插值方式)、metric(相似度计算)、optimizer(优化方法)类型;② 设置fixedImage、MovingImage;③ 设置迭代次数S、最大迭代步长、最小迭代步长等迭代参数;④ 初始化参数;⑤ 重复迭代;⑥ For i = 1 to S do;⑦ 将MovingImage结合相应的位移矩阵、插值方式进行转换得到TransferImage;⑧ 计算TransferImage与fixedImage之间的metric;⑨ 对位移矩阵进行迭代优化;⑩ End For。

图6 基于三维运动轨迹的环状伪影去除方法流程图
1.3 基于位移矩阵的FDK重建算法
本文中基于位移矩阵的FDK反投影使用的是像素驱动方法,将每个重建像素坐标投影到投影图上,获得对应投影图坐标下的值后累加到该重建像素值上。由于在单圈抖动拍摄的一圈投影图中每一个角度对应的平移台位置不同,因此需要在反投影时将每个位置位移矩阵考虑到FDK算法内,使得实际物体上同一个点在不同平移台位置时的投影值都能累加到同一个CT值上。如图7所示,以源到探测器平面的垂线与探测器平面的交点为坐标原点,源与坐标原点的连线为y轴,旋转轴为z轴。α为投影线与y轴之间的夹角,焦距为D。
确定源、探测器、旋转中心后,通过旋转物体来获得不同角度的投影值,基于位移矩阵的FDK算法主要有三步:
第一步,对物体旋转角为β的投影数据进行预处理,即投影值乘以cosα:
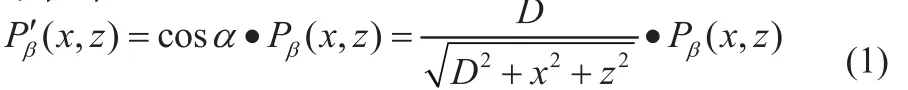
第二步,对不同投影角度的投影数据进行水平方向上的一维滤波,g(x)为一维斜坡滤波器:
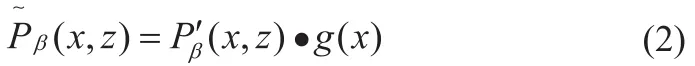
第三步,最后沿X射线方向进行三维反投影。我们定义旋转以及平移的操作为M得到:

得到某点坐标之后,我们需要将经过M变换之后的点(xM,yM,zM)做正投影到探测器上,得到此点的投影点坐标对应的上的值,将这个操作定义为B:
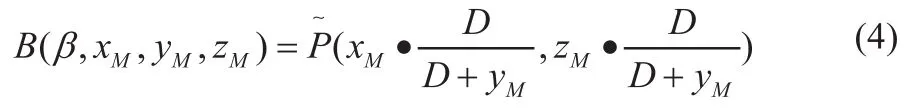
重建的CT值是各角度下通过该体素的所有角度投影的贡献之和,式(5)中N为投影角度数,因此我们得到:


图7 锥束的坐标系
2 实验及结果分析
基于三维运动轨迹的环状伪影去除算法的验证实验设计,本文采用一组仿真数据与一组离体小鼠肱骨真实数据验证算法的有效性。本文中的小鼠产地为南京市江宁区青龙山动物繁殖场,体重为24~26 g,取其肱骨进行离体拍摄实验。实验中所用真实数据由实验室已有的高分辨型显微CT拍摄获得。重建参数,见表1。

表1 重建参数
2.1 仿真结果
使用标准的三维shepp-logan模型进行了平移台移动仿真实验,平移台一共选取了四个位置,分别为P0(0,0,0)、P1(γ,-γ,γ)、P2(-γ,γ,-γ)、P3(γ,-γ,-γ),其中代表步长。本次仿真实验分为四组子实验a、b、c、d,去除环状伪影后的重建图像对应图8a~d,图8e~h分别为图8a~d的局部放大图像。实验中,分别设置a、b、c、d的步长分别为0、1、5、10。当等于0时等同于平移台没有移动,如图8a、e所示重建图像带有明显环状伪影;当等于1、5的时候,如图8b、c、f、g所示重建图像环状伪影去除效果明显,且不影响图像质量;当等于10时,如图8d、h所示,虽然环状伪影也被消除了,但是重建图像出现了一定程度的条纹状伪影。实验说明了位移大小应当尽量控制在10以内,位移过大,会产生影响图像质量的伪影。

图8 仿真结果注:a~d为移动步长r分别为0、1、5、10的重建图像;e~h为a~d的局部放大图像。
2.2 实际结果
本文对小鼠肱骨进行了高分辨显微CT成像。使用重复定位精度良好的三维平移台进行固定选取了四个位置,经过亚像素三维配准算法计算,得到这四个位置分别为(0.00,0.00,0.00)、(3.23,4.23,0.10)、(-4.10,2.30,-0.34)、(4.89,2.01,1.40)。图9a为平移台没有移动的重建结果,可以看到环状伪影明显。图9b为基于三维运动轨迹的重建结果,环状伪影得到了很好的去除,图像中没有出现因为位移而产生其他伪影。实际实验结果明显可见环状伪影减少、去环效果显著,小鼠肱骨本身结构像也符合其微结构特征,因此论证了此环状伪影去除方法在实际实验中的有效性以及可重复性。

图9 小鼠肱骨图像注:a. 环状伪影;b. 基于三维运动轨迹去除环状伪影图像。
3 结论
本文提出了一种基于三维运动轨迹的高分辨显微CT环状伪影去除方法。基于位移矩阵的FDK重建算法实现过程也可以采用先反投影,再平移的方式。但是,这种方法存在两个缺点,首先此方法需要额外的内存空间用于保存反投影后的临时重建数据,特别是对于高分辨显微CT这种数据量大的系统而言,内存消耗过大。其次平移的过程中多做了插值操作,损失了分辨率。仿真实验探讨了位移大小对于图像质量的影响,结果证明基于位移矩阵的FDK重建算法在小位移的情况下,对图像质量基本没有影响。由仿真实验以及真实实验结果可知,本文提出的基于三维运动轨迹的高分辨显微CT环状伪影去除方法在不额外增加采图时间的条件下,对于环状伪影去除效果优秀、重建速度快,对于具有复杂成像系统的透镜耦合式高分辨CT非常适用。

