响应曲面法优化石英脉型金矿尼尔森重选工艺

陈桥，陈贵民，佟琳琳，林意人，杨洪英

(1.东北大学冶金学院，辽宁沈阳，110819；2.海南山金矿业有限公司，海南乐东，572531)

重力选矿是一种利用矿石密度和粒度的差异，借助介质流动的外力作用实现不同矿物分离的过程[1]。重力选矿具有安装和能耗成本低、操作简单及环境友好等优点，被广泛应用于黄金选矿中[2]。尼尔森选矿机是一种典型的离心强化重选设备，因其能够有效回收微、细粒金而在世界范围内得到了广泛认可和应用[3]。自1980年尼尔森选矿机问世至今，已有大量的国内外学者对其分选机理及工业应用进行了研究。通常认为，影响尼尔森重选效果的因素主要有2个方面：一是原料性质，包括脉石密度、磨矿细度及矿浆浓度等；二是操作条件，包括给矿速度、相对离心力及反冲水压等。研究人员利用单因素实验、中心复合设计实验等方法探究了各个因素对尼尔森选矿机分选效果的影响，主要研究概况如表1所示。由表1可知，不同研究关于影响尼尔森选矿机分选效果的主次因素结论存在差异，这与使用的原料性质、实验方法及实验设备不同有关。文献中研究使用的原料为高品位砂金矿或者人工配制的混合矿石，具有一定的特殊性，缺少以工业金矿石为原料的实验样本。因此，本文作者以石英脉型金矿为原料，利用响应曲面法探究各因素对尼尔森选矿机分选效果影响的主次关系及交互作用，并优化分选工艺条件，以实现该金矿的高效回收。

1 原料及方法

1.1 原料性质

本试验所用原料为海南某金矿。对原矿石中Au，S及SiO2进行定量分析可知：原矿石中金品位为9.8 g/t，S和SiO2质量分数分别为0.65%和62.19%，可见该矿石属于低硫石英脉型金矿。利用X线衍射分析、光学显微镜及扫描电镜等分析方法，对原矿石进行工艺矿物学研究，结果表明：该矿石的主要脉石矿物为石英、白云母及绿泥石，质量分数分别为49%，37%和8%；主要金属矿物为黄铁矿，质量分数约为1%。金矿物主要为自然金，赋存状态为包裹金、粒间金和裂隙金，分别占48%，43%及9%。金矿物粒度分布较广，粗粒金、中粒金、微粒金以及细粒金的质量分数分别为33%，18%，23%和26%。

1.2 试验设计

响应曲面法是一种利用数学建模统计分析输入参数和输出变量之间关系的试验设计及优化方法，它通过对特定的点进行局部试验，利用回归的方法拟合出全局范围内各因素与结果之间的函数关系，从而定量分析各因素及其交互作用对结果的影响，并通过优化分析获得各因素的最优水平值[12]。采用响应曲面法可以快速有效地确定各因素及其交互作用对金回收率的影响，并得出该矿石尼尔森重选的最佳条件。

影响金矿石尼尔森分选效果的因素主要包括脉石密度、磨矿细度、矿浆浓度、给矿速度、相对离心力及反冲水压力。磨矿细度、相对离心力及反冲水压对精矿品位及金回收率影响较大，因此选取磨矿细度、相对离心力和反冲水压3个参数进行响应曲面分析，分别用x1，x2和x3表示，响应曲面选择的实验因素水平和编码见表2。尼尔森选矿机具有产率低、富集比高的特点，并且尼尔森重选精矿通常用摇床进一步精选，故以金回收率作为响应曲面优化的评价指标。

表1 尼尔森选矿机分选效果的影响因素研究概述Table 1 Summary of literature on influence of various factors on separation effect of Knelson concentrator

表2 响应曲面设计因素和水平编码Table 2 Independent variables and their levels used for response surface methodology

利用软件design expert8.0进行试验设计，将选择的因素和水平输入系统，按照Box-Behnken组合方法设计出试验方案，如表3所示。

表3 试验设计及结果Table 3 Experimental design matrix and results

1.3 试验步骤

原矿石经颚式破碎机(EP-3)破碎后，利用XMQ-350×160型球磨机磨矿，使磨矿细度分别达到40%，65%和90%，利用激光粒度仪(BT9300H)分析磨矿产品粒度，结果如图1所示。研究使用选矿设备为KC-MD3，每组试验使用原矿2 kg，矿浆质量分数为40%，给矿速度为500 g/min。各组试验结束后，收集尼尔森精矿，过滤、烘干、测质量并分析精矿品位；尾矿均匀取样后烘干，检测尾矿品位，并计算金回收率。

图1 样品粒度分布曲线Fig.1 Particle size distribution of sample

2 结果与讨论

按照设计方案进行试验，结果见表3。试验所得精矿品位为139.64～242.8 g/t，对应的金回收率为66.06%～81.92%。

2.1 选择响应模型

采用Design-Expert软件对试验结果进行分析，结果如表4所示。考虑到本试验中金回收率受多因素影响，对表4中的多种模型的显著性、失拟项及相关性数据进行综合分析，选择采用二阶模型来近似模拟。

表4 模型统计表Table 4 Model summery statistics

2.2 响应模型的方差分析及模型建立

对金回收率的二阶模型进行方差分析以及显著性检验，结果见表5。在方差分析中，P小于0.05则视为模型显著[13]，由表5可知，二次模型P＜0.000 1，失拟项P大于0.05，表明该模型适应性很好，拟合精度高。多项式模型的拟合质量用R2表示，多元相关系数R2越大，说明相关性越好，模型拟合良好的相关系数应不小于0.80[14-15]。该模型中相关系数(R2=0.984 6)表明模型方程与实验数据接近，调整后的确定系数(R2=0.964 7)也说明了模型的显著性。变异系数(CV)表示实验进行的精确程度，是评价实验可靠性的指标，CV越低，实验的可靠性越高[16]，该试验中CV较低(1.21%)，说明试验结果可靠性较高。一般认为，信噪比大于4的测量方法具有足够的精度，视为合理[17]，本模型中信噪比为21.005，证明模型适用。

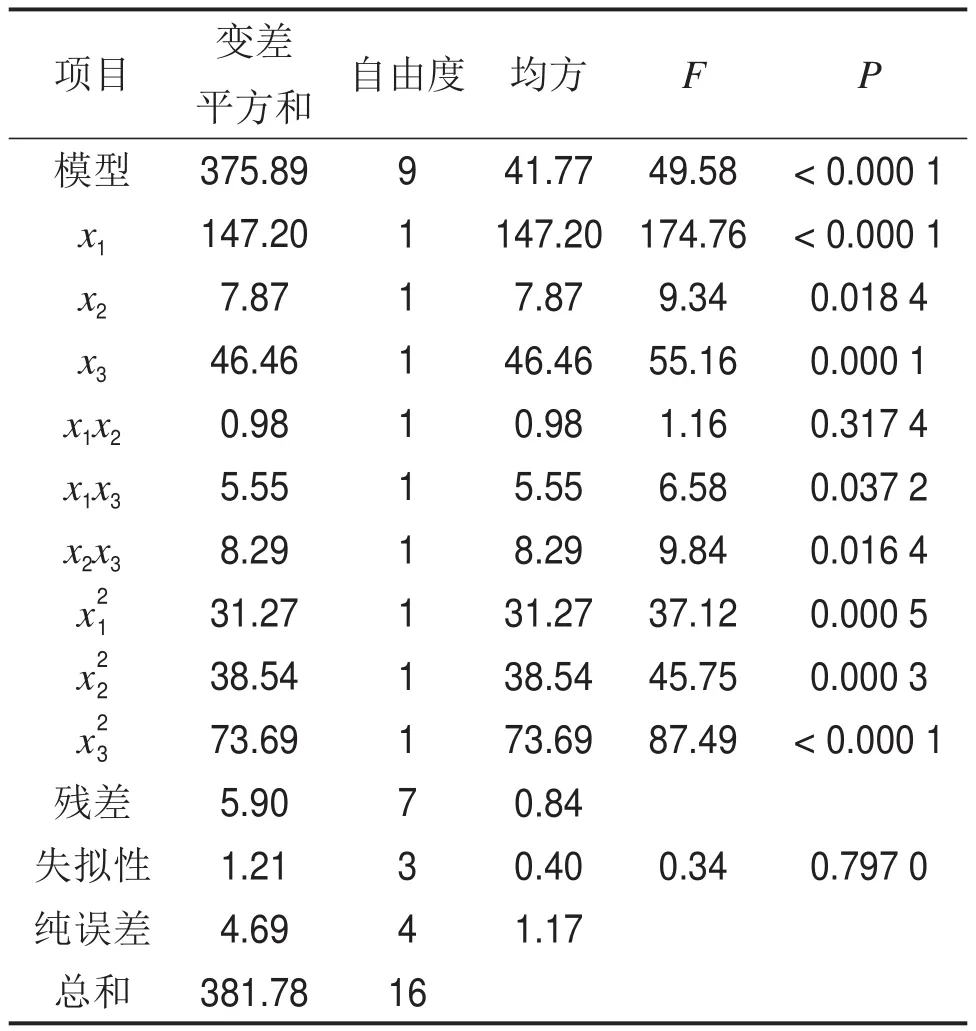
表5 金回收率的二次模型方差分析结果Table 5 Analysis of variance for response surface quadratic model of gold recovery

通过软件分析计算，得出金的回收率关于变量的拟合方程为

金回收率模型的残差正态概率分布及预期值试验值的比较分别如图2和图3所示。由图2可知，回收率模型的残差散点几乎分布在一条直线上，且在模型残差正态概率图中的中间概率上分布的残差散点比在两边的分布密集，残差落在区间(-2，2)以外的概率为0，说明模型拟合效果非常好。由图3可知，回收率的预测值与试验值的散点近似分布在一条直线上，说明试验值和预期值有很高的契合度。综合以上分析可得，通过响应面试验方法建立的回收率预测模型可靠。

图2 回收率模型残差正态概率Fig.2 Normal probability versus internally studentized residuals

图3 回收率预测值与试验值对比Fig.3 Predicted values versus experimental values of recovery ratio

2.3 响应曲面分析

图4～6所示为自变量对因变量的响应曲面及等高线图。响应曲面图是由各影响因素交互作用下的响应值构建的三维空间曲面，它可以直观地描述各试验因素的变化对响应值的影响，若曲面坡度较陡，则该因素对响应值的影响较大，反之则影响较小。因素之间交互作用的显著程度可通过等值线图直观地表现出来，其等值线轮廓图越接近圆形，表示因素的交互作用越不显著[18-19]。

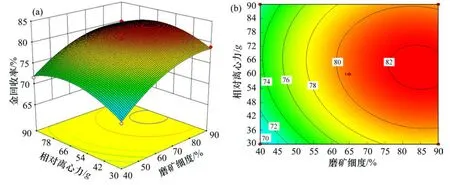
图4 磨矿细度与相对离心力对回收率的交互影响Fig.4 Response surface and contour plots for effects of particle size and relative centrifugal force on gold gravity

图5 磨矿细度与反冲水压对回收率的交互影响Fig.5 Response surface and contour plots for effects of particle size and water pressure on gold gravity

图6 相对离心力与反冲水压对回收率的交互影响Fig.6 Response surface and contour plots for effects of relative centrifugal force and water pressure on gold gravity

由图4(a)可知，当磨矿细度一定时，金回收率随着相对离心力的增大先增加后减小，但总体变化幅度不大，可见相对离心力对金回收率影响相对较小。当相对离心力一定时，金回收率随着粒度变细先快速增加，后增加速度变缓，并达到最大值，该极值出现在中等离心条件(55～70g)及较细的粒度(磨矿细度为75%～90%)范围内。图4(b)所示为等值线图，其形状近似为圆形，说明磨矿细度与相对离心力的交互作用不显著。

图5(a)所示为反冲水压和磨矿细度对回收率影响的响应曲面。从图5可以看出，当磨矿细度一定时，金回收率随着反冲水压的增大先增加后减小，在反冲水压4～16 kPa范围内金回收率增加速度较快，而在反冲水压16～28 kPa范围内降低速度较慢。这是由于反冲水较小时分选床层被压实，分选不完全，随着水流量增加，流态化床层形成，金回收率快速达到最大值；反冲水压进一步增加会将部分细粒金带入尾矿中流失，导致金回收率降低。保持反冲水压一定，随着矿石粒度变细金回收率逐渐增加，且变化范围较大，表明磨矿细度对金回收率影响较大。由图5(b)可知：中等值线图轮廓呈椭圆形，磨矿细度与反冲水压的交互作用较为显著。

当磨矿细度为65%时，反冲水压和相对离心力对回收率影响的响应曲面如图6(a)所示。由图6(a)可知，反冲水压对回收率的影响大于相对离心力对回收率的影响，最大值所在区域对应的反冲水压为14～24 kPa，相对离心力为55～75g。由图6(b)可知，相对离心力和反冲水压的交互作用对金回收率的影响最显著。

综合方差分析和响应面分析可知，3个因素对金回收率的影响从大到小顺序为磨矿细度、反冲水压、相对离心力；相对离心力与反冲水压的交互作用最显著，反冲水压与磨矿细度的交互作用次之，而相对离心力与磨矿细度的交互作用不明显。

2.4 过程优化

利用软件优化功能得出模型预测的最优条件如下：磨矿细度为83.17%，相对离心力为64.68g，反冲水压为18.55 kPa，该条件下金回收率的预测值为82.48%。为了实际操作方便，调整磨矿细度为83%，相对离心力为65g，反冲水压为19 kPa，在此条件下进行验证实验，得到金回收率分别为81.96%，82.44%及82.58%，平均值为82.33%，与模型预测值接近，说明该预测模型在本试验的研究范围内是合理的，证明应用响应面法能够快速有效地对该金矿尼尔森选矿机重选工艺参数进行优化。

3 结论

1)磨矿细度对金回收率影响最大，反冲水压次之，相对离心力对金回收率影响最小；相对离心力与反冲水压的交互作用最显著，磨矿细度与反冲水压的交互作用次之，而相对离心力与磨矿细度的交互作用不显著。

2)通过模型预测最优实验条件为：磨矿细度83.17%，相对离心力64.68g，反冲水压18.55 kPa。在最优条件下，金回收率的预测值为82.48%，试验平均值为82.33%，与预测值相差0.15%，表明在本试验研究范围内该模型是合理有效的。