数形结合思想在高中数学解题中的运用

陈丁潇

数形结合就是将更直观的图形与更抽象的数学语言结合起来，将形象思维与抽象思维紧密结合起来，通过对图形的有效处理，充分发挥直觉思维对抽象思维的支柱作用，有效地实现具体图像与抽象概念之间的转换和联系，变难为易，并提取出来。图像知识可以转化为可视化。根据解决问题的实际需要，定量关系问题可以逐渐转化为相关问题。基于此，本文针对高中数学解题中数形结合思想应用的方法展开深入的分析和研究，促使我们能够在实际的高中数学学习当中掌握更多的解题思路和方法。

“数”与“形”总是不可分割地结合在一起，这是一种抽象和直观的表现。在高中数学中，“数”和“形”是两个最基本的数学概念，高中数学的学习体系是围绕两个基本概念发展起来的。数与数相结合的思想不仅能提高学生解决问题的能力，而且对培养学生的数学素养也有很大的作用。在高中数学中，数与数结合的思想是解决数学问题的重要方法。熟练掌握和运用数与数相结合的思想，将抽象的数学概念信息与直观的图形相结合，简化思维过程，可以大大提高问题解决的效率。由此能够看出，加强对高中数学解题中数形结合思想应用的方法的研究具有十分重要的作用和现实意义。

1 高中数学解题中数形结合思想应用的意义

如果我们在学习过程中使用数字和数字相结合的思想，这将有助于我们的高中生相应地转换一些更模糊和困难的概念，并使知识点的概念更具体和更容易理解。这样，当我们学习和记忆时，我们可以进一步缩短记忆时间，达到事半功倍的效果。因为高中数学中有许多种类的函数公式，它们还包括对定义域的性质、单调性、范围等的背诵和理解。如果我们使用数字和数字的组合来记忆和理解，我们可以加深学习的印象，并有助于我们成就的发展。

如果我们在学习数学的过程中仅仅依靠死记硬背，不仅不利于我们数学成绩的提高，也影响了我们学习数学的兴趣，这在学习数学的过程中产生了负面影响，不能促进我们数学成绩的提高。但是，如果我们在学习过程中将数字和图形相结合的思想应用到数学学习过程中，这不会让我们在学习数学的过程中感到枯燥乏味，也将极大地帮助我们高中生提高学习数学的信心。因此，为了提高我们高中生学习数学的兴趣，我们可以在学习数学的过程中使用数和数相结合的思想，这有助于帮助我们促进数学成绩的提高。

2 高中数学解题中数形结合思想的应用

2.1集合问题

在高中数学的解题当中，集合问题是比较典型的题型，在解决相关集合问题的过程中经常会涉及到Venn图和数轴的使用，能够将较为抽象化的问题变得更加的具体化，并且能够将问题转化为最简化，更好的帮助我们学生使用最快的方法解决问题，促进我们在实际的解题当中掌握更多的数学知识。

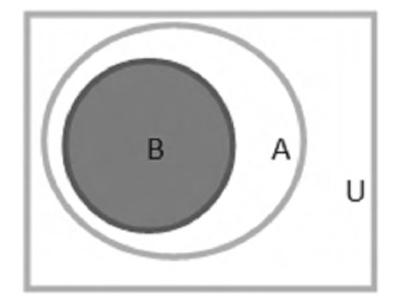
例如：已知全集U=N，集合A={x|x=2n，n∈N}，B={x|x=4n，n∈N}则，U=（      ）。

解：有题目可知，B是A的真子集，在解决这道题的过程中就可以使用Venn图辅助解题。如右图。

2.2方程、不等式问题

由于不等式的概念比較抽象，学生就可以根据数形结合思想帮助自己理解不等式的概念，让我们学生能够更加质感的理解不等式的概念。在学习数学方程以及不等式相关知识的过程中，可以转换成为两个函数的交点问题，不等式问题就可以依照条件和问题转化成为函数，然后分析题目虽具有的几何意义，并且能够从图形方面寻找到解决问题的方法。

例如：求解的过程中，可以将其转化为图像交点的相关问题，可以先画图，能够得出。

2.3绝对值问题

正确理解和掌握计算原理是解决数学问题的关键，在计算更复杂的计算机时有一些问题，很多时候我们都很难理解计算原理，这就导致计算混乱，无法计算出正确的数学答案。因此，我们学生在利用数形结合思想解决绝对值的问题上时，可以将问题转化到数轴上，然后根据绝对值的性质能够获得一个准确的范围，进而能够获得绝对值问题的答案。

例如：|x|>a，（a>0），求解。

在解题的过程中就可以根据数轴（如右图所示），然后再根据绝对值的性质就能够得到：一点到另一点的距离，解得x<-a或者是x>a。

结语：综上所述，将数与数结合的思想渗透到高中数学课堂学习中是一项重要的要求。在高中数学课堂学习中，如果能帮助学生掌握数与数结合的相关思想，不仅能培养学生分析和思考问题的能力，还能更好地提高学生学习数学的能力。因此，学生应该学会如何将数形结合的思想渗透到解题中，帮助学生简化复杂的数学问题，形象化抽象的数学概念，澄清数学计算问题，形象化隐含的数学规律，促进学生更灵活地运用数形结合的思想。

（作者单位：山东省肥城市第一高级中学）