基于改进果蝇优化的压电精密定位平台迟滞Bouc-Wen模型辨识

王龙飞，邓 亮，刘 萍

上海电力大学 自动化工程学院，上海200090

1 引言

近年来，随着航天、纳米生物工程、微电子、精密制造等领域的快速发展，压电执行器在微纳米定位受到越来越广泛的关注[1-2]。然而，输出位移与驱动电压之间的迟滞非线性限制了其在快速高精度定位系统中的推广[3-4]。为此，研究人员采用各种数学模型描述迟滞非线性，如Preisach模型[5]、Prandtl-Ishlinskii模型[6]，Bouc-Wen模型[7]和Jiles-Atherton模型[8]等。Bouc-Wen模型可描述各种迟滞非线性和迟滞动态行为，在压电精密定位平台、磁流变阻尼器、音圈电机等迟滞系统建模中得到广泛应用[9-10]。然而，由于模型复杂的非线性特性和辨识参数较多，其参数辨识已成为具有挑战的问题[11]。

利用Bouc-Wen模型对压电精密定位平台实施建模需辨识五个参数，其参数对滞环形状的影响呈现强非线性，很难根据大量的数据总结具体模型的参数范围。据此，Bouc-Wen 模型在磁性材料领域的应用相对较少。随着有效数值算法的发展，Bouc-Wen 模型参数辨识已更为准确，模型的动态性能有望得到改善[12-13]。文献中讨论了几种实现这一目标的方法，包括解析法、高斯-牛顿法、单纯形法、简化梯度法和扩展卡尔曼滤波[14-15]。由于迟滞非线性辨识的复杂性，随机优化被认为是一种很好的解决策略。近年来，已有学者采用遗传算法[16]、粒子群优化[17-18]、差分进化[19-20]等算法辨识迟滞非线性模型。此外，Laudani等人运用度量-拓扑进化优化算法获得了Bouc-Wen模型参数[21]。尽管前述方法已产生准确的辨识结果，但依然可开发新颖的群智能优化算法以获得更快的收敛速度和更高的辨识精度。为此，本文提出一种改进的果蝇优化算法（IFOA）对压电精密定位平台迟滞Bouc-Wen模型参数进行辨识。

果蝇优化算法（Fruit fly Optimization Algorithm，FOA）是由中国台湾学者潘文超于2011年6月提出的一种全局优化智能算法[22]。该算法已成功应用于科学和工程领域，并在求取函数极值、微调Z-SCORE 模型系数、优化广义递归神经网络参数和支持向量机回归参数等方面有着广泛应用。与其他智能优化算法相比，FOA具有简单易懂、调节参数较少、计算量小、寻优能力较强且寻优精度较高等优点。因此，设计改进的FOA 并将其应用于Bouc-Wen模型的参数辨识具有重要的研究意义。迄今为止，尚未有基于改进果蝇优化的压电精密定位平台迟滞Bouc-Wen模型的辨识报道。为了提高算法的优化性能，本文从种群多样性保持、迭代搜索步长设置和后期精确寻优三个方面对FOA 进行改进，提出改进的果蝇优化算法（Improved Fruit fly Optimization Algorithm，IFOA），使算法寻优性能得到提升并将其成功应用于压电精密定位平台Bouc-Wen模型的参数辨识。

2 果蝇优化算法

FOA 是基于果蝇觅食行为而推演出的一种寻找全局最优解的群智能优化算法。果蝇本身具有敏锐的视觉和嗅觉系统，对漂浮在空气中的气味颗粒具有超强的感知能力。果蝇个体利用其嗅觉系统能迅速地向接近食物源的方向飞去，同时其利用敏锐的视觉系统发现同伴聚集的位置，并向该位置飞去。果蝇寻找食物的过程是不断地从食物味道浓度低的地方飞向浓度高的地方，直至发现食物源为止。

果蝇群体迭代搜索食物的过程如图1 所示，Fly group 表示果蝇群体的初始位置；Fly1,Fly2,Fly3为果蝇个体的搜索方向；Dist 为果蝇个体与原点之间的距离；S 表示果蝇个体的味道浓度判定值，其为距离的倒数；Smell 为果蝇个体对应的味道浓度值，其是味道浓度判定值的函数。

根据果蝇的觅食特征，果蝇优化算法的具体步骤如下：

步骤1 初始化果蝇群体位置(xp,yp)，并给出种群规模SizePop 和最大迭代次数MaxIter。

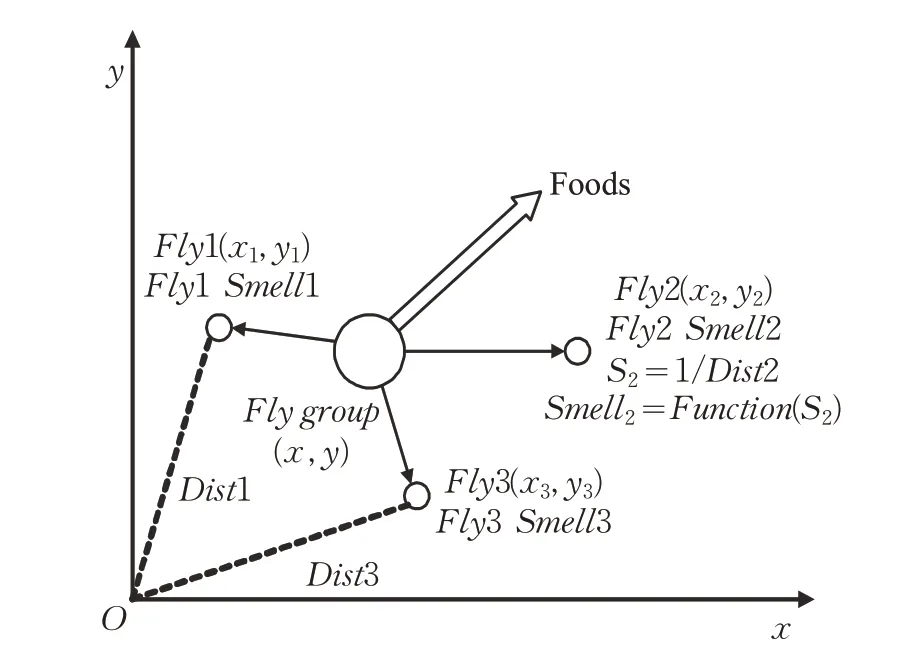
图1 果蝇群体迭代搜索食物示意图

步骤2 赋予果蝇个体随机方向和距离，利用嗅觉寻找食物。

式中，i=1,2,…,SizePop,xi,yi为第i 个果蝇种群的初始位置；randx,i,randy,i为[0，1]内的两个任意随机数。

步骤3 估算果蝇个体距原点的距离Di并计算味道浓度判定值Si：

步骤4 将Si代入味道浓度判定函数（即适应度函数f）得到果蝇个体的味道浓度值Smelli：

步骤5 找出味道浓度最佳的果蝇个体（这里取最小值）并记录该果蝇的最佳气味浓度值bestSmell 和在此种群对应的标号bestIndex：

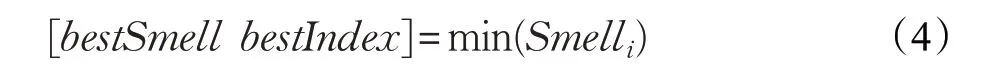
步骤6 将最佳气味浓度值bestSmell 记为Smellbest，并记录相应的位置坐标和最佳气味浓度判断值bestS。果蝇群体将利用视觉飞向该位置：

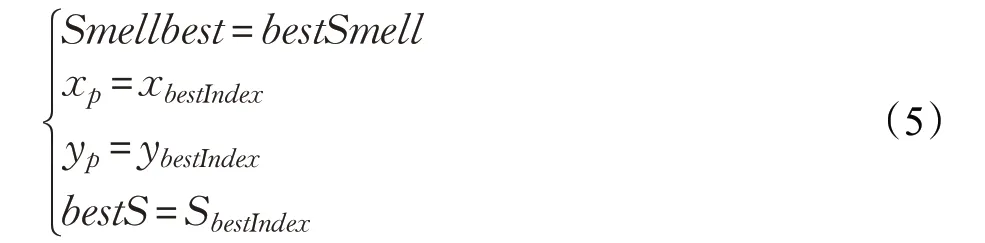
步骤7 算法完成初始化，开始进入迭代寻优过程。

对步骤2～5重复执行，判断当前最佳味道浓度值与上一代最佳味道浓度值的大小，若当前最佳味道浓度值小于上一代最佳味道浓度值（此时目标函数是求最小值），则执行步骤6，否则继续进行迭代，直至达到最大迭代次数为止。

3 改进的果蝇优化算法

原始的FOA结构简单，代码易于实现，相比于其他智能算法，具有调节参数少，计算速度快，寻优精度高等优点。然而，原始的FOA依然存在以下缺陷：

（1）在算法寻优时，每次迭代果蝇都飞向适应度值最高的果蝇个体，这在一定程度上降低了果蝇群体的多样性。一旦该果蝇个体位于局部最优值附近，算法极易陷入局部最优解。

（2）算法每次迭代都取固定步长。搜索步长若取值较大，在迭代前期会加快算法的寻优速度，但迭代后期，过大的搜索步长会使算法在最优解附近徘徊，始终达不到精度要求；若取值较小，则大大降低算法寻优速度，使得算法的整体寻优性能下降。

（3）在后期的精确搜索中，果蝇个体位置通过x、y坐标的微小变化进行更新。当算法的优化函数为多维函数，且多维的目标解彼此不在同一数量级，则此更新方法不会使目标解进一步向精确解靠近，使得算法只能保持当前精度而不会进一步提高精度。

因此，本文重点从群体多样性、迭代搜索步长和后期精确搜索三个方面对FOA进行改进。

3.1 群体多样性改进

遗传算法利用交叉因子产生代表新解集的种群，这一过程将使该种群所产生的后代种群比前代种群更能适应当前环境，从而逐渐搜索到问题的全局最优解。同时，后代种群与前代种群相结合，在很大程度上增加了种群多样性，使得算法不易陷入局部最优值。

在改进的果蝇优化算法中，将上次迭代随机产生的果蝇群体两两交叉组合，得到的新群体代入味道浓度判定函数，并与交叉前的最优个体进行比较，选出交叉前后的最优个体作为下次迭代的初始位置。通过交叉操作不仅能增加迭代过程中果蝇群体的多样性，跳出局部最优，同时还能加快收敛速度。交叉操作的公式如下：

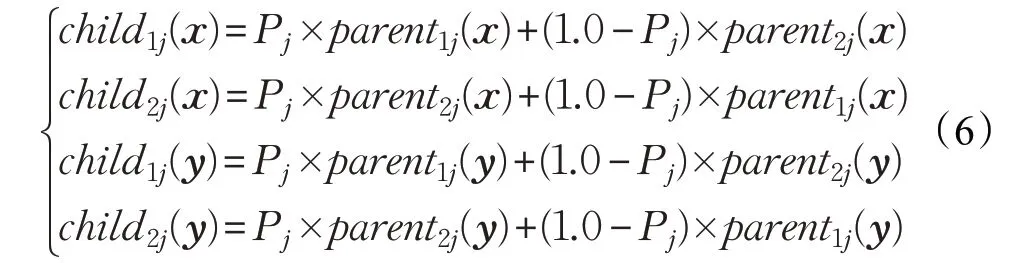
式中，j=1,2,…,d；x,y 为d 维位置向量；childk(x),childk(y)和parentk(x),parentk(y)分别表示子代群体和父代群体位置；k=1,2 分别为群体中前半部分和后半部分成员；P 表示d 维随机分布的任意数向量，其中的每一个分向量都在[0，1]中取值。

3.2 迭代搜索步长改进

根据果蝇优化算法的基本原理，果蝇群体的随机搜索方式为：

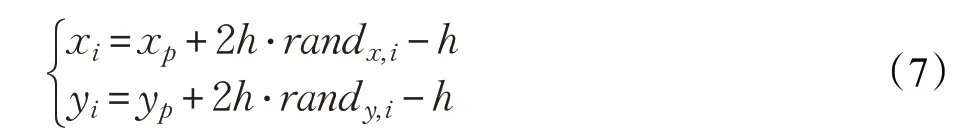
式中，h 为搜索步长，randx,i,randy,i为（0，1）内的两个任意随机数（当x,y 为多维时，rand 为多维向量）。

3.3 算法后期寻优策略改进

在此，加入对味道浓度判定因子S(i)的寻优机制，即果蝇在以后的迭代过程中，不再对其位置x,y 进行每一次更新，而是直接对味道浓度判定因子bestS 更新。这样，合理设置对判定因子的寻优步长，即能向最优解进一步靠近。

假设上一次迭代寻优后得到的最佳味道浓度判定因子为bestS，且bestS 已在最优解附近。设置判定因子的寻优步长时，根据bestS 的数量级进行针对性的步长调整。此搜索方法的搜索机制为：

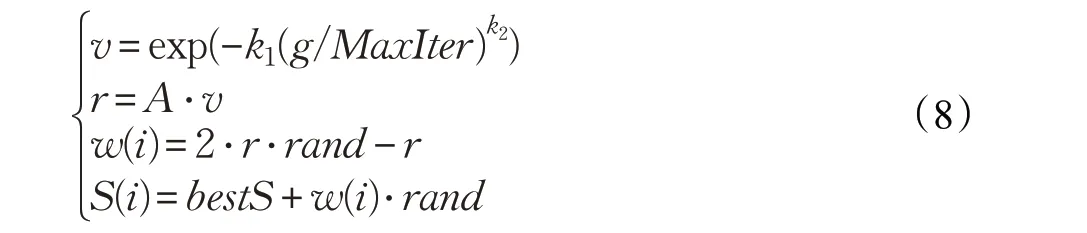
式中，v 为惯性权重函数；g 为当前迭代次数；k1,k2为设定常数；r 为根据前一步迭代得出的寻优步长；A 为bestS 的数量级，可在Matlab 中通过指令floor(lg(bestS))求得；w(i)为当前迭代次数下的搜索方向；S(i)为味道浓度判定因子。

3.4 具体步骤

结合3.1～3.3 节中对果蝇优化算法进行的改进，改进的果蝇优化算法具体步骤如下：

步骤1 初始化果蝇群体位置(xp,yp)，并给出种群规模SizePop 和最大迭代次数MaxIter。

步骤2 赋予果蝇个体随机方向和距离，利用嗅觉寻找食物。

式中，i=1,2,…,SizePop,xp,yp为第i 个果蝇种群的初始位置；randx,i,randy,i为[0，1]内的两个任意随机数。

步骤3 估算果蝇个体距原点的距离Di并计算味道浓度判定值Si：

步骤4 将Si代入味道浓度判定函数（即适应度函数f）得到果蝇个体的味道浓度值Smelli：

步骤5 找出味道浓度最佳的果蝇个体（这里取最小值）并记录该果蝇的最佳气味浓度值bestSmell 和在此种群对应的标号bestIndex：

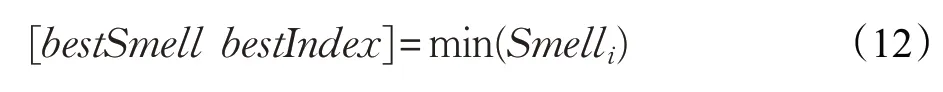
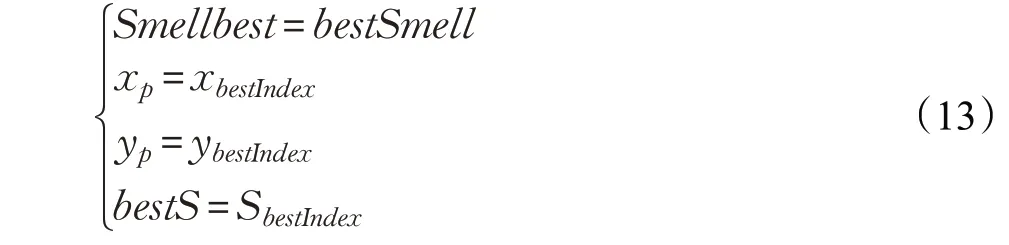
步骤6 对此果蝇群体进行交叉操作，得到新的种群位置x1i,y1i，重复执行步骤3～5，找出味道浓度最佳的新果蝇个体：

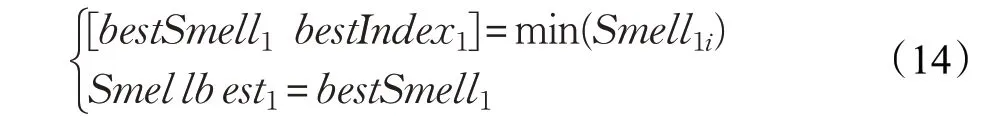
步骤7 若Smellbest1＜Smellbest ，则更新原来的最佳位置：

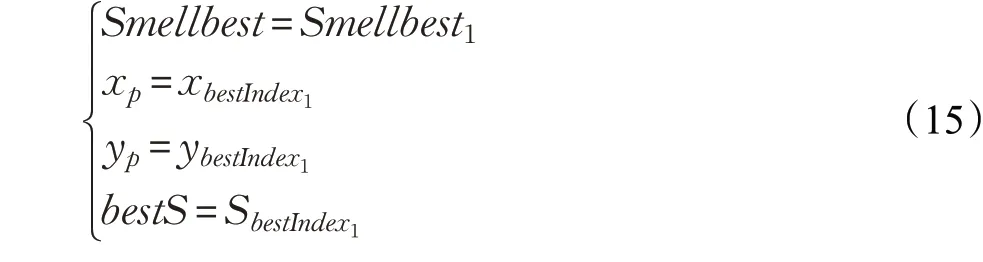
步骤8 若Smellbest1＞Smellbest ，则保持下一次迭代的初始位置xp和yp不变。

步骤9 引入自适应搜索步长hi，并将其代入果蝇个体利用嗅觉觅食的公式中：

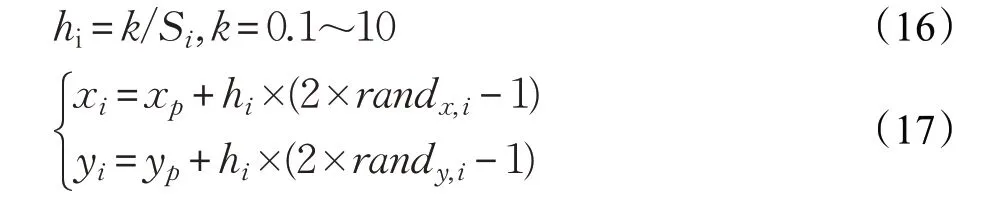
步骤10 进入迭代寻优，重复执行步骤2～8，直至达到最大迭代次数为止，输出寻优结果bestS。

步骤11 启动算法后期精确搜索机制，设置新的最大迭代次数，并将得出的寻优结果bestS 作为精确搜索的初始值。将步骤2～3更改为式（18）所示S(i)后，继续执行步骤4～8，直至达到设置的最大迭代数为止并输出bestS 新的值。

4 压电精密定位平台Bouc-Wen模型参数辨识

压电精密定位平台的迟滞非线性是指执行器升压和降压曲线之间存在位移差，其在很大程度上会影响压电执行器的控制精度。Bouc-Wen模型既包含了非线性阻尼，又包含了非线性刚度，能对各种光滑的迟滞曲线进行描述。本章将改进的果蝇优化算法应用于压电精密定位平台Bouc-Wen模型的参数辨识，通过建模比较，验证辨识结果的准确性。

4.1 Bouc-Wen模型建立

压电精密定位平台的迟滞曲线如图2所示，图中虚线为曲线上最大和最小位移之间的连线。压电精密定位平台的迟滞曲线可看成是该虚线与曲线上的迟滞分量之和：

式中，x(t)为平台输出位移，u(t)为系统输入电压，kv为输入电压与输出位移之间的比例常量，h(t)为迟滞分量，x0为初始位移（一般默认为0）。其一阶导数为：

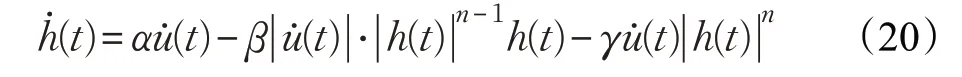
式中，kv、α、β、γ 和n 为待求参数。

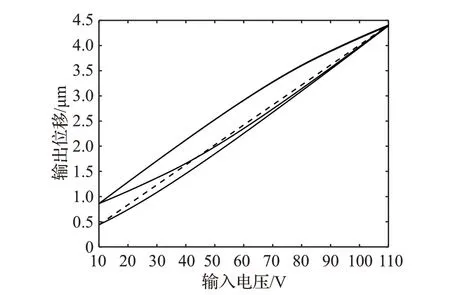
图2 压电精密定位平台输入电压与输出位移的迟滞曲线

4.2 模型参数辨识

取均方根误差作为改进果蝇优化算法中味道浓度判定函数，即：

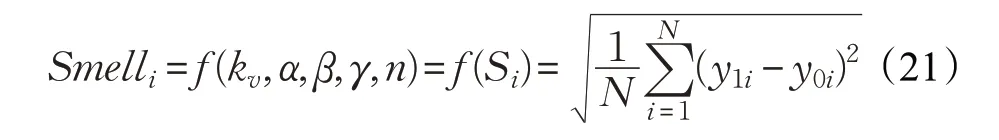
式中，y1i和y0i为第i 个采样时刻的模型输出位移和实测位移，N 为采样个数。将最大迭代次数设置为100，种群规模设置为20，具体辨识步骤如3.4节所示。

4.3 实验验证

压电精密定位实验平台如图3所示，包括RHAC系列精密定位控制器和压电精密定位平台。RHAC 系列控制器具有过流、过热、短路保护，高频率响应、极低的静态电压纹波，其内置标准模拟PID 闭环控制，可加快闭环调整速度，保证闭环压电精密定位平台的最佳控制精度，并具有开、闭环切换功能，可以开环或闭环方式对压电精密定位平台控制。RHAC 系列控制器输出电压稳定性＜0.1%FS/8 h，电压分辨率35 PPmFS±10%，电压监控分辨率0.1%FS，输出电压范围0～140 V，输出电压纹波≤10 mV ，平台输出的非线性为0.1%FS（标定行程）。计算机通过RS232 串口与控制器相连，通过控制器上位机软件获取输出位移。输入电压设计为V=60-60e-0.35tcos(2πe-0.06tt),采样频率100 Hz，仿真时间5 s。

为了直观地反映改进果蝇优化算法步骤的合理性，将其分为三部分加以比较。IFOA1、IFOA2、IFOA 分别为引入交叉因子、引入交叉因子和自适应搜索步长和提出的改进果蝇优化算法。将输入和输出数据保存为原始数据，选取前2 s和后3 s数据集分别作为训练和泛化数据，采用FOA、IFOA1、IFOA2和IFOA对Bouc-Wen模型参数辨识，具体步骤同3.4节。种群规模设置为30，迭代次数为100 次。表1 给出了FOA、IFOA1、IFOA2 和IFOA 辨识出的压电精密定位平台Bouc-Wen 模型参数和适应度值。

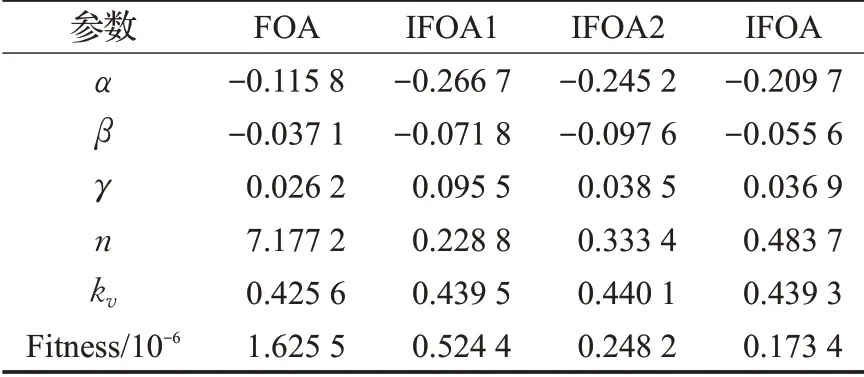
表1 四种优化算法辨识的Bouc-Wen模型参数和适应度函数值

辨识结果如图4～7所示，图4为算法收敛特性比较，图5 给出了输出位移跟踪曲线，相应的迟滞环如图6 所示，辨识出的模型的输出位移与实验数据之间的误差如图7。从辨识结果可见，IFOA 建模效果明显优于IFOA1、IFOA2 和FOA，充分证明了改进方法的有效性和辨识优势。

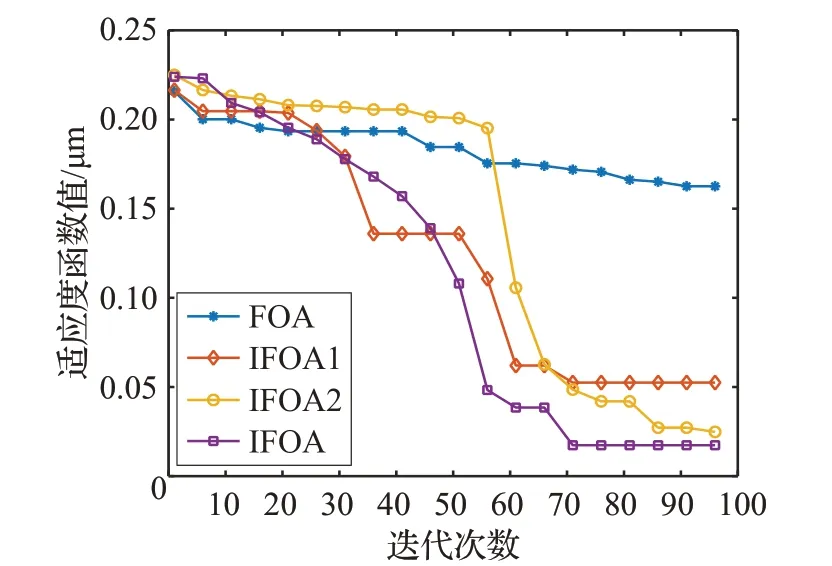
图4 算法收敛特性比较

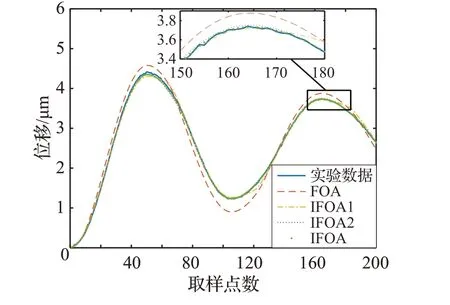
图5 不同算法对应的位移跟踪曲线

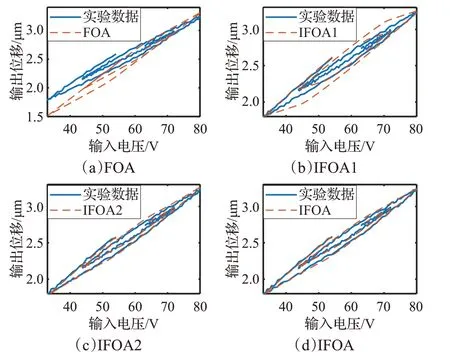
图6 不同算法下辨识出的迟滞环与实验数据的对比

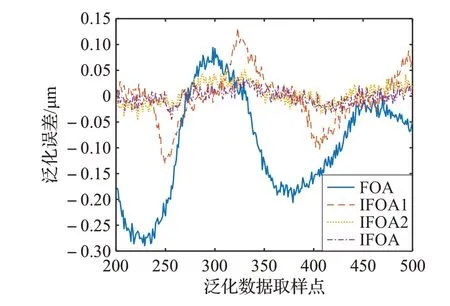
图7 不同算法对应的位移跟踪误差曲线

5 结束语

本文采用广泛应用于迟滞系统的Bouc-Wen模型描述压电精密定位平台迟滞非线性特性，提出一种改进的果蝇优化算法对其参数实施辨识。为了验证所采用模型和相应参数辨识方法的有效性，对压电精密定位实验平台迟滞非线性特性进行了实验建模。研究结果表明，所提出的改进果蝇优化算法能将建模平均绝对值误差控制在0.1 μm以内。