悬浮水轮原理及外界微扰下的系统稳定性研究

尹一凡

(北京航空航天大学 自动化科学与电气工程学院，北京 100191)

1 现象分析

在生活中经常看到以下现象：在靠近朝上喷水的水柱边缘小心放置一个轻质物体，在一定条件下，物体将在悬浮的同时开始旋转。通过实验观察出以下特点，一方面，在水流的冲击下，水轮在竖直面内快速旋转，并且转速维持在一个稳定值附近，同时液体冲击水轮后出现飞溅现象，之后较强的系统稳定性使得体系可以在一定程度上抵抗来自外部环境的干扰。通过观察高速摄像机照片发现，液体在接触点与物体发生作用。先以液体流速为变量进行了实验，得出了实验结果如图1所示，从中发现，液体主要集中离开点与液体流速有着很大关系，随着流速的增加，液体的离开由集中流淌离开向铺洒的方式变化，现象也更为剧烈，而且液体的流淌也更多地从两侧偏向中间竖直轴线。

通过对水流的分析，猜想，水流流向可以分为沿竖直轴线和从轮球两侧流动前进这两种情况，即为图2中ABC这三条方向，这些方向与物体的外形有着显著关系。对于图2左图所举例的水轮而言，其边缘垂直的壁面使得AC两股水流可以忽略不计，可以视水流为全部经过B的途径。而对于图2右图所示的情况，即物体两侧不完全垂直，如圆球、梭型等物体，这时水流不仅能通过B途径，也会通过AC途径前进。

通过对A/C途径进行分析，其作用除了使B途径液体量减少外，还在于马格努斯效应的产生。马格努斯效应的含义为：当一个旋转物体的角速度矢量与该物体飞行速度矢量不同向时，存在垂直于这两个矢量的横向力，使物体的飞行轨迹发生偏转，横向力的方向可由右手定则确认[1]。

图2 水轮俯视、平视图Fig.2 Top view and head-up display of water turbine

图3 马格努斯效应示意图Fig.3 Schematic diagram of Magnus effect

在A/C途径下，物体在旋转角速度下还有着相对运动速度，按照马格努斯效应，产生了如图3所示的横向力，因此需要在平衡方程中进行相应的公式修正。同时，在稳定性上，该作用力也使得物体在水平方向上趋向靠近水流冲击点，使物体不易脱离接触，纵向上也使得物体维持高度所需的液体作用力更小，使稳定性增强。

2 水柱与水轮的位置关系

对水轮而言，必须要先由其边缘与水柱相接触，使水柱冲击水轮的下侧，使其产生向上的作用力，使其能够保持不掉落。同时，如果作用位置恰好为水轮的正下方，则水轮在理想条件下不会旋转且会在所处位置保持平衡。而在实际情况里，这样的平衡为不稳定平衡，因而不再赘述。

在单侧受到水流冲击时，从水平方向来分析，冲击点与水轮重心应同处于右视基准面，否则从前视基准面上分析来看，水轮所受重力与水柱的作用力不在同一条直线上，无法满足平面力系平衡条件，水轮也就无法处于平衡状态。

3 水轮的受力状况

3.1 仅在冲击点处存在摩擦力

此时的受力分析如图4所示。

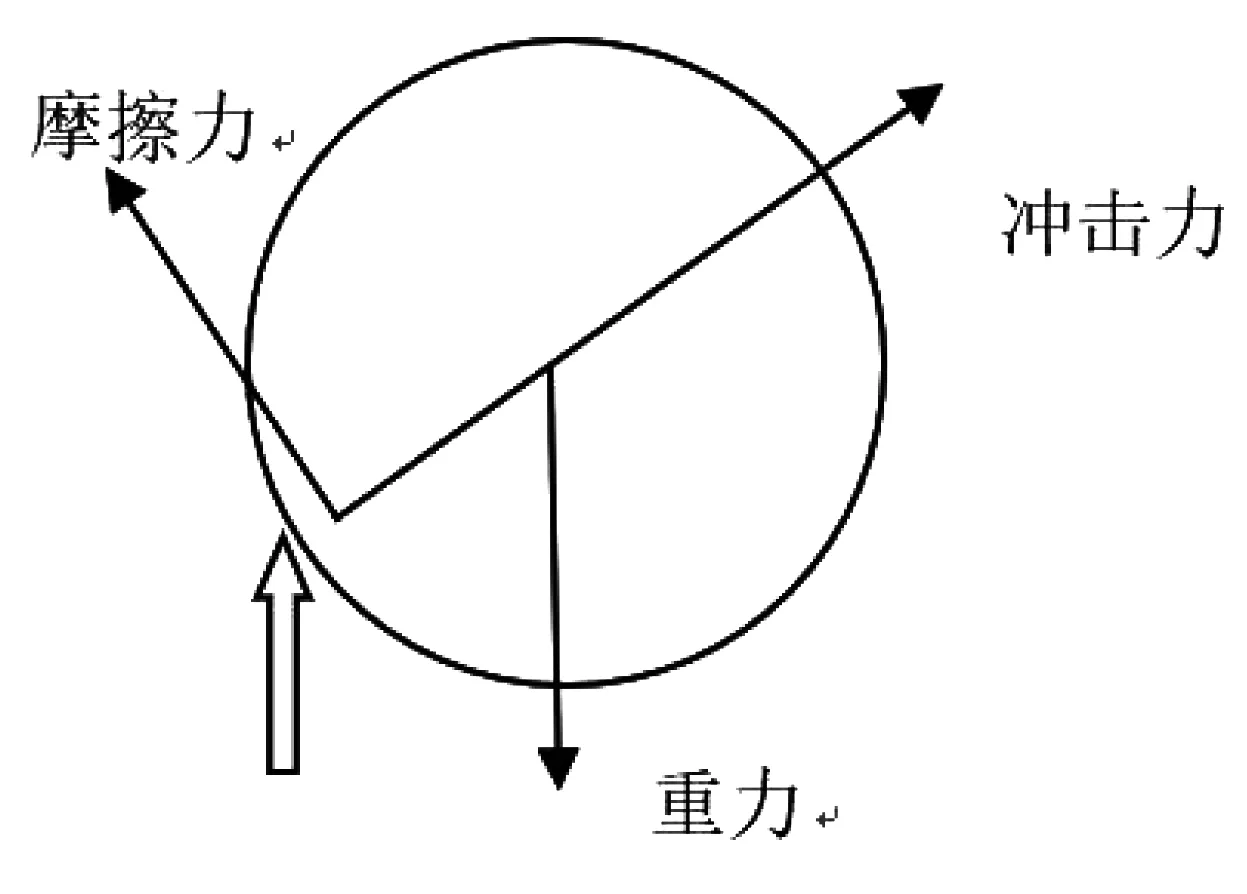
图4 受力模型假设Fig.4 Stress model assumptions

假设冲击点与圆心连线与水平线夹角为θ，水轮转动的角加速度为α，F为冲击力，Ff为摩擦力，R为水轮半径，m为水轮质量，此时对其进行受力分析：

may=mg+Ffcosθ+Fsinθ=0

max=Fcosθ-Ffsinθ=0

Jα=FfR

其中：

从x、y方向上的受力情况来看，摩擦力的存在可以使水轮质心在铅锤平面上保持平衡，但由于角加速度α的存在，使水轮旋转不断加快，在较长时间后，在冲击点的切线方向上，水轮与水柱的速度相同。也就是说，两者间最终会不存在相对速度和相对运动趋势，这样摩擦力也就不会产生了。由此看来，从最开始的仅有冲击力到加入单一的摩擦力来试图解决问题的模型是不成功的，因此要引入其他的作用力[2]。

3.2 水对水轮有着多处摩擦力作用

一般情况下，两个刚体的碰撞会使得两刚体快速接近并迅速分离，中间可能产生了短时间的法向或切向作用力，而在根据这一点做出的以上两种分析均不能解释悬浮水轮的现象，因此在新模型中开始考虑水的形变带给水轮受力分析的影响。

考虑到水轮与小球在曲面构型上的相似性，以小球为例进行水柱的冲击实验。通过实验发现，当水柱冲击小球的下侧面时，水柱并没有出现像之前猜想的那样直接弹开，而是吸附在了小球表面，以至于将其完全包裹。

图5 小球模型实验实物图(1)Fig.5 Physical figure of small ball model experiment (1)

如图5所示，如果继续考虑摩擦力的作用，则可以得出以下物理模型：

在初始状态下，水柱冲击水轮后，两者的切向速度差使得带动水轮旋转，当到达平衡状态时，水轮转速保持不变，而水柱在接触点处的切向速度仍大于水轮的切向速度，在这种情况下，摩擦力对水轮产生了转动加速的力矩。然而，部分水附着在水轮外侧，水轮带动水的作用力的反作用力产生的反向力矩，使得水轮能够在固定的转速保持平衡[3]。

内侧圆代表水轮，外侧圆代表水轮外缘附着的水。同时，为简化模型，假设，水在同一角度对应的区域内是均匀分布的，而考虑到水在外缘的纵向上可能并不是均匀分布的，可以假设水的单位质量(质量的角密度)与角度θ满足函数ρ=φ(θ)。

针对水处于圆心水平线上下两种情况，分别做出了以下受力分析，其中，T代表水轮对水的吸附力，Ff代表水轮对水的摩擦力，dmg或G代表任意微小角度dθ所对应的水的重力。

3.2.1 水在中心线下时(θ<0)

受力分析如图6所示。

图6 θ<0时受力分析Fig.6 Stress analysis when θ<0

在此过程中，Ff可能出现反向情况，便只设向上为正方向，由此可以建立以下关系式：

mat=-cosθG+Ff

anm=T-sinθG-N

G=φ(θ)gθdθ

根据力学方程，得出动力学规律如下：

an=ω2R

根据微分变换可以得出以下式子：

联立方程可得：

T-sinθG-N=ω2Rm

其中，当水速大于水轮转动速度时：

Ff=μN

由此，便可以根据初始的冲击点所对应的角度θ0与水柱接触时的初始速度来求解出与之相对应的两者共速时的角度θ1与速度ω1。

对于摩擦力Ff的求解：

3.2.2 水在中心线上时且在右侧时(θ>0)

受力分析如图7所示。

图7 θ>0时受力分析Fig.7 Stress analysis whenθ>0

根据力学方程，得出动力学规律如下：

atm=Ff-cosθG

anm=T-N+sinθG

在这一段上，因为水轮转速固定，如果假设附着在水轮上的水流速度处处相等，则ω可视为不变且与水轮转速相等，此时：

at=0

an=ω2R

联立方程可得：

T-N+sinθG=ω2Rm

cosθG=Ff

因为质量与角度的关系式得到：

Ff=cosθgφ(θ)dθ

3.2.3 水在中心线上时且在左侧时(θ>0)

由于当水被吸附到水轮的左侧时，其受力分析与水流在右上侧时完全对称，而由于水可能会在这一段上离开水轮，因此假设水在θ2时离开水轮，而过程中摩擦力的表达式与之前完全相同。

3.2.4 综合以上，整体对水轮进行分析

综上所述，针对对水的分析以及牛顿第三定律得出了，水轮所受摩擦力的关系式为(以逆时针方向为正)：

从水轮的所受外力来看，水对水轮吸附力的力矩为0，所以仅有摩擦力可以提供力矩。此时，若以轮质心为轴心进行分析，摩擦力的力矩只有为0时，水轮才可能平衡。构建力矩力矢的平衡方程为：

T冲cosθ0=1

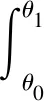
T冲sinθ0-Mg=0

其中，水轮与水流的吸附力T是与水的流速、温度、密度等相关的函数[4]。通过分析得出，作用力T是该作用力可以分为康达效应下的空气压力与水轮外缘壁对液体的沾附作用的合作用力。接着对空气压力进行分析，由伯努利方程得出：

考虑到重力对空气的作用可近似忽略不计，同时贴近液体表面的空气流速也与液体流速近似相同，便可得出空气压力的表达式：

T可简化为Fair(θ)与沾附作用的合力模型，而后者则可以通过材料间的特性进行分析，在此便不再赘述。

φ(θ)也取决于液体流速与水柱流量的关系，为简便运算，可假设T与φ(θ)均为常数，此时：

由此，可认为该模型是成立的。

3.3 通过动量分析水轮平衡

在之前的三个模型中，主要依靠对水轮及水的受力分析来解决问题。现在，通过构建模型和冲量定理来对当球转速过高而使水飞溅的情况进行定性分析。在之前的模型中，水覆盖在水轮表面，当水流速加快后，水流就不再局限于包裹水轮，而是在随着水轮转动的过程中沿着水轮的切线飞溅出，如图8所示，其原理比较接近于研磨金属板时飞溅的火花。

图8 小球实验实物图片(2)Fig.8 Picture of ball experiment (2)

在这种情况下，可以对水轮及其上面的水做整体定性分析。在冲击过程中，水轮始终受到竖直向下的重力带来的冲量，因此水必须要提供给水轮以竖直向上的冲量，而两者在相同时间内大小相等。由牛顿第三定律可知，水轮与水的作用力与反作用力大小相等，方向相反。在这段时间里，水柱I2受到来自水轮竖直向下的冲量，这一分析重点在于确保合动量在水平方向上的分量为0。由于水流最终的动量方向具有不确定性，只要所有动量矢量相加的合动量方向为竖直方向，则水轮在水平方向上的稳定即可得到解释。

4 水轮的抗微扰分析

水轮稳定系统可能会受到各种外部干扰，可以分为轴向力、竖直力、水流干扰等。

4.1 抗轴向力干扰

4.1.1 干扰恢复

当水柱受到来自侧面的轴向力干扰时，水轮会发生偏向轴向力方向的倾侧，水流方向也会随着水柱的倾侧而发生倾侧。根据之前依照冲量定理的分析，当受到向右的轴向力时，水流方向也会向右倾斜，此时水流便会反作用于水轮向左的水平分冲量，水轮在水平方向上便可以得到平衡，并在位移上得到回位。除了从冲量角度进行分析，也可以从作用力角度来分析。当水轮受到水平向右的冲量时，水轮相对于其所附着的水会产生向右的相对速度，此时水轮便会受到来自水的向左摩擦力以使水轮保持平衡。

4.1.2 恢复的局限性

通过分析可以看出，只有被附着的水流沿着水柱方向被充分加速再被甩出去才能产生足够大的反向冲量使水轮平衡。在此过程中，水的右向加速需要一定时间，如果加入冲量的时间过短，水根本来不及变向加速，水轮也就无法在水平冲量角度上保持平衡。同时，如果外力的干扰力过大，使摩擦力无法平衡外力，则物体会加大倾斜，直至完全偏离平面，此时的恢复力也就无效了。此外，如果外力的作用点过于靠近冲击点，产生的位移使得水柱与水轮的接触出现偏离，就会导致附着水流减少，甚至完全脱离水流接触，使系统根本无法依靠水流与水轮作用力来恢复。

4.2 抗纵向力干扰

4.2.1 干扰恢复

在竖直方向上，向下的作用力可以视为水轮重量的增大。从突变时刻到水轮不断被重新调整变速到新的平衡转速过程中，水轮会在竖直方向上做直线运动，直至达到新的稳定。而向上的作用力则可以视为水轮质量的突变减少，分析过程基本与向下时相同，但水轮的质心运动方向和转速变化趋势会相反。

4.2.2 恢复的局限性

作用力向下时，主要考虑留给系统的空间是否足够去调整。如果水轮距离地面高度过小，则水轮会在重新达到平衡状态前撞击地面，系统也就无法平衡。而当作用力向上时，平衡的主要问题在于作用力与水轮重力及水柱流速的关系。如果作用力大于重力或理论平衡的位置超出了水柱所能到达的最大高度，系统也无法实现新的平衡。

4.3 水流干扰

4.3.1 干扰恢复

水流发生变化主要为暂时性断流，水流加强或减弱。对于暂时断流情况，水轮在某一时刻只会受重力作用而脱离水流，此时，水轮会出现短时间的落体过程。而当水流加强时，水轮受到的冲击力会突然变强，此时会产生向上的冲量，其位置会上升。在不考虑冲击力带来水平位移的情况下，高度会上升到新的冲击点处，水流量与原先处相同。水流减弱时分析同理。

4.3.2 恢复的局限性

对于断流的存在，在极短时间内，水轮的受力会存在局部缺失的情况，而且其上面水流的分布也会出现变化，水轮在水平方向上就会出现冲量差，会造成微小的水平偏移。当水流速过大时，水轮可能会被短时激增的冲击力冲出接触平面，而造成系统无法复原的平衡破坏。当水流速过小时，水流的作用力可能无法使水轮保持转动或悬浮，会造成新的失衡。

5 针对文中假设的校正

本研究对水轮表面的水流流量分布做出了常量假设，现作出更细致的校正：

设：在角度θ处飞溅的水量为f(θ)，如果忽略初始冲击时损失的水量且水柱的水量为函数Q(θ)，则其满足方程：

6 结论

通过上述分析表明，水轮与水柱的冲击点处在水轮质心所在纵剖面，否则将无法在位置上满足平衡条件。在平衡受力模型的建立中，排除错误模型，通过理论证明得出合理的“包裹式摩擦力”物理模型，并通过合理假设得出的动力学方程表示出平衡时的物体状态，由定性分析得出平衡时的冲量条件。在抗微扰分析中，通过多种外界干扰假设，分别探究了水轮在不同情况下的动态稳定性。最后，对水流量的常量假设进行校正，用以在日后的实验中测出相关量后对方程进行修正。