Cu75Ni25合金平衡固-液界面的微观结构

王贤洋 吴丙心 汪 昊 尤静林 吴永全

（1.省部共建高品质特殊钢冶金与制备国家重点实验室，上海 200444；2.上海市钢铁冶金新技术开发应用重点实验室，上海 200444；3.上海大学 材料科学与工程学院，上海 200444）

在冶金及材料等领域，金属凝固是最重要的相变过程。固-液界面（crystal-melt interface，CM interface）作为金属凝固发生的第一现场，对凝固过程中的形核和长大都至关重要，因此对固-液界面结构和性质的研究一直都是物理、化学以及材料学等领域的热点。但由于固-液界面深埋凝聚相之中，很难通过试验的手段进行精确定位和直接观察［1］，因此目前对固-液界面微观结构的研究基本是通过计算机模拟的方法来完成。这其中尤以分子动力学（molecular dynamics，MD）模拟的应用最为广泛［2］。

目前，关于固-液界面的描述主要基于界面区（interface region）的概念，包括界面区的定位以及各种结构或属性在界面区的连续变化。对于界面区的定位，通常采用所谓“10% ～90%”原则［3］。针对固液界面的微观结构描述，主要依照分层结构及层内有序度（layering and in-plane ordering）框架［4-5］，即将固-液界面区沿法线方向切成几个薄片，对每个薄片进行平均属性的统计，由此表征平均属性沿法线方向的一维（1 dimension，1D）衰减规律；同时在每个薄片内部又可以精确分析二维有序度的分布并以图像方式进行显示和描述。

目前，金属固-液界面结构的研究主要集中于纯金属，如 Al、Mg、Fe等［6-8］，合金的界面研究相对较少。CuNi合金是全成分范围的匀晶，单质Cu和Ni都是FCC结构，在元素周期表中相邻，半径相近，固-液相都可无限互溶，因此CuNi合金具有很高的应用价值和科学研究意义，已成为近年来的研究热点之一［9-11］。近年来，已报道的关于CuNi合金平衡界面的模拟研究主要集中在溶质吸附［12］、动力学系数［13］、界面能［14］等方面，对 Cu和Ni元素在界面区的分配及其结构表征的区别等研究还较少。为此，本文通过分子动力学模拟，以键取向序参数（bond orientational order，BOO）［15］为主要结构表征手段，对 CuNi合金平衡界面的微观结构进行分析。

根据相图计算，取Cu75Ni25合金成分点，且固液占比接近的平衡点（固相占比Xs＝58.6%，固相中 Ni浓度 xNi，s＝30.3%，液相占比 Xl＝41.4%，液相中 Ni浓度 xNi，l＝17.5%），获得比较持续稳定的固-液界面，有利于对界面结构的研究。

1 模拟方法

1.1 MD模拟概述

本文采用美国Sandia National Labs开发的LAMMPS软件［16］进行MD模拟。采用嵌入原子势（embedded-atom method，EAM）［17-18］描述 CuNi合金原子之间相互作用势：

式中：α和β分别表示中心原子i和邻近原子j的原子种类；Fα为元素α的嵌入函数；ρβ为β原子的电子密度函数；rij为原子i和j之间的距离；φαβ为α和β的对势函数。

该势函数及其参数的正确性在CuNi合金相变的研究中已经得到了很好的验证［19］，在此基础上，采用该势函数对CuNi合金进行了MD+MC（Monte Carlo）相图计算，结果与试验相图［20］相吻合（如图1所示）。

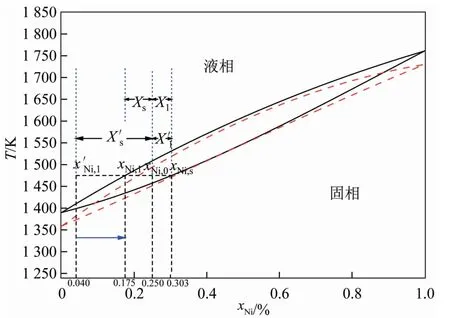
图1 CuNi合金相图（黑色实线为模拟结果，红色虚线为试验值［20］）Fig.1 Phase diagram of CuNi alloy（solid black line represents the simulated phase diagram，red dotted line represents the experimental value［20］）

模拟采用三维周期性边界条件。MD步长为2 fs，运动方程积分采用蛙跳法，采用 Noose-Hoover恒温器和Andersen恒压器控制温度和压力。模拟体系为长方体，其中垂直于界面的方向为z轴。模拟分为两部分，对应两个不同系综：恒温恒压系综（NPT）的升降温过程和恒压恒焓系综（NPH）的两相平衡过程。本文选择3个低指数晶向（［100］、［110］和［111］）作为固-液界面的法线方向，这3个晶向体系大小见表1，其中nx、ny、nz分别为沿x、y、z轴方向的元胞个数。固-液界面平行于x-y面，因此z方向的长度要远大于x和y方向，以保证体系中形成足够区域的两个体相。

表1 ［100］、［110］、［111］晶向体系大小Table 1 System size of［100］、［110］、［111］orientations

整个模拟过程概述如下。（1）先构建0 K下的完美Cu75Ni25晶胞，在0～t1阶段（如图2所示）升温至1 610 K（NPT系综，P＝1 bar），略高于目标温度，如图3（a）所示，体系保持完好的FCC晶格；（2）在 t1～t2阶段（图2），左部原子固定，右部原子（占比约20%）继续升温至2 000 K，待其完全熔化，然后在t2～t3阶段（图2）降温至1 610 K且保持熔态，形成液相约占X′l＝20%的固-液共存体系（图1），图 3（b）为该共存构型；（3）随机抽取等量的左部固相Cu原子和右部液相Ni原子，分别改为对应的Ni和Cu，直至固相中的Ni达到目标浓度 xNi，s＝30.3%（图 1），液相对应的 Ni浓度约为 x′Ni，l＝4.0%（远低于平衡液相浓度，见图1），因该过程属于等量互换，所以始终维持体系的总浓度 xNi，0＝25%不变，图 3（c）为该起始构型；（4）改变体系能量，在 t3～t4阶段（图 2）进入NPH系综（P＝1 bar）趋衡弛豫，直至体系达到固-液两相平衡，图3（d）为最终的平衡构型。固-液平衡时，液相Ni原子浓度达xNi，l＝17.5%（图1），固相和液相之间的比例不再发生变化，约为58.6∶41.4（与图1相图中的杠杆比例一致），同时温度趋于平衡温度。需要说明的是，基于动力学因素，第（3）阶段中固相初始浓度为平衡浓度xNi，s，而液相初始浓度远低于平衡浓度x′Ni，l。在MD的模拟时域范围内，固相原子扩散非常困难，可认为几乎不扩散，而液相原子扩散则容易得多。因而在第（4）阶段，体系会通过熔化固相使液相浓度上升，最终达到与固相平衡的浓度，同时温度达到平衡温度。

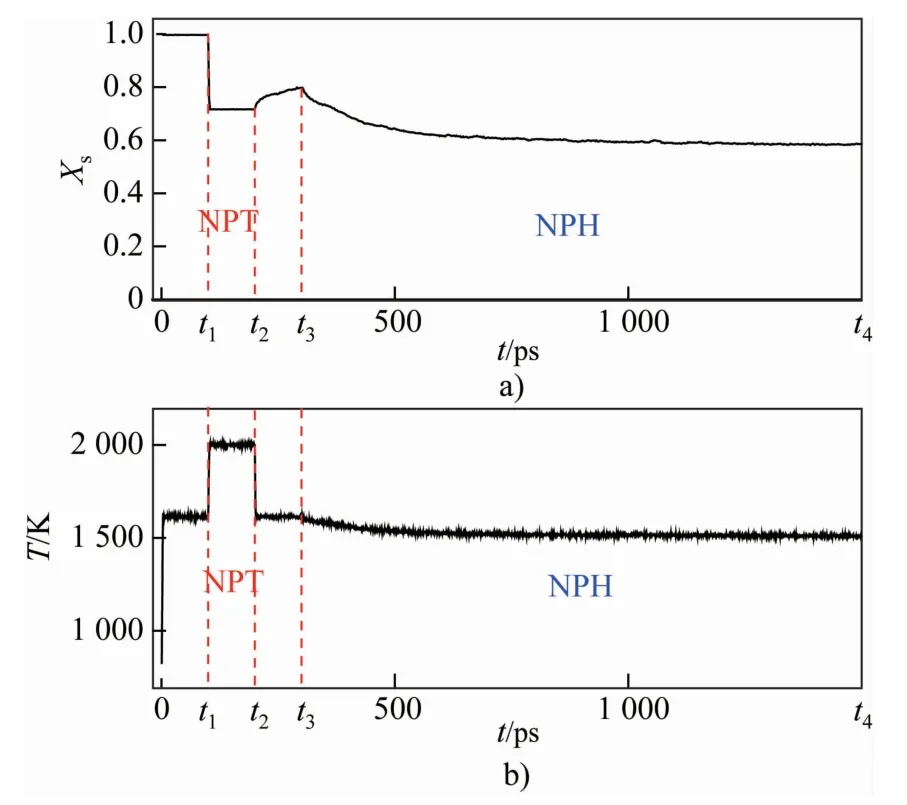
图2 （a）固相原子占比及（b）体系温度随时间的变化（［100］方向）Fig.2 Variation of proportion of（a）solid atoms and（b）temperature with time（［100］direction）

1.2 结构表征方法

采用BOO参数法［15］进行原子标定。对于原子i定义一个复向量：

图3 ［100］方向4个阶段的最终构型（红色代表Cu原子，蓝色代表Ni原子）Fig.3 Four final configurations at the ends of 4 steps in［100］direction（red represents Cu atom，blue represents Ni atom）

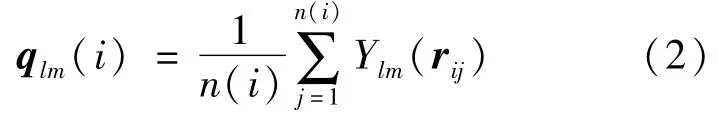
式中：n（i）是原子 i的第一近邻原子数，Ylm（rij）是与原子i成键的原子j的l重球谐函数，rij是从原子i到原子j的键向量，m为整数，其取值范围为-l～l。根据l取值不同，式（2）可以描述原子之间不同程度的对称性。通过评估原子局部环境的对称性参数，来判定原子的结构。

为了区分固、液相，Ten Wolde等［21］引入序参数Sij：

式中：q6m（i）为式中l＝6时的6重复向量，*为共轭复数。序参数Sij为原子i和原子j之间的局部相关性。当Sij大于某个临界值（通常为0.5［22］）时，则认为原子i和原子j是“相连或成键”的。据此，定义一个Frenkel数（用ξ表示）来指代与中心原子“成键”的原子数。当某个原子的ξ小于阈值，ξ（i）＜ξc（阈值 ξc＝7），则认为该原子为液相原子；否则为固相原子。

2 结果与分析

2.1 熔点及其各向异性

试验获得［100］、［110］和［111］3个方向的常压平衡熔点分别为 1 508.31、1 514.92、1 523.35 K，平均值为1 515.53 K，与相图中对应的温度1 475 K很接近。与［100］方向相比，［110］和［111］方向的熔点分别高 6.61和15.04 K，说明 Cu75Ni25合金与纯金属 FCC-Al［7］、BCC-Fe［8］一样，存在各向异性。该结果初步解释了在Cu75Ni25合金降温过程中，有的晶向发生提前凝固的现象［10］。例如，［100］和［110］方向迟于［111］方向凝固，这与 Ni3Al的结果相同［23］，即［111］方向是优先凝固和生长的方向。这是因为凝固温度相同时，［111］方向的过冷度较大，即形核和长大驱动力较大。

固、液两相平衡后，继续弛豫300 ps，对平衡构型进行结构分析。在NPH系综下，3个方向体系能量、体积都保持稳定。表2为体系平衡时的液相浓度 xNi，l、固相浓度 xNi，s及液相占比 Xl、固相占比Xs，固、液比与相图对应的值（固相占比Xs＝58.6%，固相中 Ni浓度 xNi，s＝30.3%；液相占比Xl＝41.4%，液相中 Ni浓度 xNi，l＝17.5%）基本相同。

表 2 体系平衡时液相浓度 x Ni，l、固相浓度 x Ni，s及液相占比X l、固相占比X sTable 2 Equilibrium concentrations of liquid phase x Ni，l，solid phase x Ni，s，and the percentages of liquid X l and solid X s %

2.2 界面属性及宽度

采用沿界面法向的密度、序参数及浓度分布表征Cu75Ni25合金固-液界面的微观结构。以数密度为例，其定义为［24］：

式中：Vz＝LxLyΔz是切片体积，Lx和 Ly分别是 x轴和y轴方向的box尺寸，Δz是切片沿z方向的厚度。＜Nz＞是每个切片内的平均原子数。Δz的取值通常等于或远小于沿界面法线方向的固相层间距（比如Δz＝0.2Å），这样或展现固相平均属性，或展现固相的结构周期性；但不能太小，否则热振周期会体现而掩盖结构周期［3］。

图4为3个方向的数密度、6重对称序参数q6、Frenkel数 ξ、Ni原子浓度 xNi及质量密度 ρ的分布。其中数密度采用了小切片厚度Δz＝0.2 Å，其他属性均采用大切片厚度，并又设定了两套厚度：第 I套为 Δz［100］＝1.8Å，Δz［110］＝1.3Å，Δz［111］＝2.1Å；第 II套的 3个值均是第 I套的 2倍。这样设置的原因是有的晶向固相切片存在晶面间隔周期的现象。

从图4（a）可以看出，数密度分布在固相中的周期性很好，在液相区则基本趋于恒定，体现了固相的结构有序和液相的结构无序。相对而言，［111］方向的固相区域数密度周期性最强，这与该方向的层间距最大有关（［100］层间距为1.7～1.9Å，［110］层间距为1.2～1.4Å，［111］层间距为2.0～2.2Å）。此外，从固相的周期结构向液相均一结构的渐变过程正对应着所谓的界面区（interface region），如图中灰色区域所示，每个共存体系都有2个界面区。

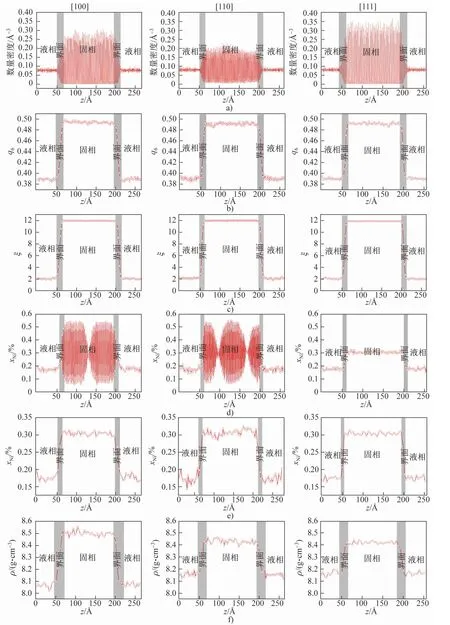
图4 Cu75 Ni25合金3个界面方向的（a）数密度（Δz＝0.2Å）、（b）6重对称序参数 q6（第Ⅰ套 Δz）、（c）序参数 ξ（第 I套 Δz）、（d，e）Ni原子浓度 x Ni（第 I套 Δz和第Ⅱ套 Δz）及（f）密度 ρ（第Ⅱ套 Δz）分布Fig.4 Distributions of（a）number density（bin size is 0.2Å），（b）q6（first set ofΔz），（c）ξ（first set ofΔz），（d，e）x Ni（first set ofΔz and second set ofΔz）and（f）ρ（second set ofΔz）profiles of the crystal-melt interface of Cu75 Ni25 alloy in different orientations

图4（b～d）为（BOP）6重对称序参数 q6、Frenkel数ξ和 Ni原子浓度 xNi分布（第 I套 Δz值）。针对q6和ξ，固相和液相分别对应的值都趋于恒定，而界面区呈过渡性变化，这种过渡与hyperbolic tangent曲线相符合。分析薄片的Ni原子浓度xNi发现，3个方向液相Ni原子浓度都趋于恒定。但［100］与［110］方向的固相Ni浓度存在一高一低现象，且间隔分布，起伏不一，而［111］方向的浓度趋于恒定。显然，沿［100］与［110］方向的固相存在两种晶面，即高Ni晶面和高Cu晶面，这是造成其浓度间隔分布的本质，固相原子层间距不为恒定值是造成Ni原子浓度起伏的主因。为此，取第II套Δz值再次统计Ni原子浓度xNi分布（如图4（e）所示），发现固相浓度趋于恒定，其值为上述相邻两切片的平均值。此外，在第I套Δz的浓度曲线中，［100］和［110］方向还出现了宏观波动，这种宏观波动正是固相热声子振动（thermal phonon fluctuation）的直接体现。对比数密度、q6、ξ和Ni原子浓度分布所确定的界面区厚度，发现Ni原子浓度分布确定的界面区厚度明显小于其他性质确定的界面区厚度，这是合金固-液界面不同于纯金属单质固-液界面的一个显著特征。

图4（f）为质量密度（（第 II套 Δz）分布，可见其固相和液相的平衡值附近波动很大，说明1 515.53 K高温造成的热声子振动十分剧烈，但该振动仅对密度产生影响，对结构对称性的影响（q6和ξ）不大。最后，无论何种属性，从固相到液相的过渡都是在界面区实现的，其线型完全符合双曲正切（hyperbolic tangent）函数，这就是所谓固-液界面的核心特征：diffuse nature。下文选取aq6（平均6重对称序数）和ξ来考察其diffuse nature，并据此估测界面区最重要的表观属性——界面区厚度。

根据试验数据，计算获得aq6和ξ的分布，采用双曲正切函数［3］进行拟合：

求得A、B、C、D参数值。然后根据拟合结果获得最大值ymax与最小值ymin，再依据“10%～90%”原则［3］定位界面及其宽度δz。图5即按照该思路分析获得的aq6结果，从而得出固-液界面宽度分别为9.25和8.73Å。

图5 ［100］方向序参数aq6分布及其双曲正切拟合结果（圆心为试验数据，实线为拟合曲线）Fig.5 Distribution of direction sequence parameter aq6 and its hyperbolic tangent fitting results along［100］direction（circle represents experimental data and solid line represents fitting line）

上述处理都是针对某个单一快照的构型进行的，为获得统计效果，最终的界面宽度是对300 ps时间长度的统计平均值，见表3。如上所述，同一样本存在两个界面，且两个界面宽度一般都存在差异。比较表3中数据可以发现：不同方向界面宽度存在各向异性。即无论采用aq6还是ξ标识的界面宽度，始终存在 δz［100］＞δz［110］＞δz［111］的规律，该结果与典型单金属固-液界面（如FCC-Al、FCC-Ni等［25］）的各向异性一致。另外还发现，采用不同属性表征的宽度值差异较大，以ξ为标准计算得到的界面宽度普遍比aq6的界面宽度小1.1～1.5Å。Gan等［26］也采用“10% ～90%”原则，以密度和势能为标准，计算得到Fe（100）-Li界面宽度分别为5.83和5.67Å，相差0.16Å。

表3 3个方向的界面宽度（以aq6和ξ为标准）Table 3 Widths of two interfaces in three orientations（taking aq6 andξas standards） Å

3 结论

本文采用NPH系综MD方法，模拟了Cu75-Ni25合金的平衡固-液界面结构及其相关属性。发现［100］、［110］和［111］3个方向的平衡熔点不同，说明Cu75Ni25合金和纯金属一样，其熔点存在各向异性。统计了平衡构型的数密度、6重对称序数q6、Frenkel数ξ、Ni原子浓度以及质量密度的分布曲线，均展示了固-液界面的diffuse nature，该性质如文献描述，可用双曲正切函数进行精准拟合。此外，作为合金的原子浓度去光滑渐变获得的界面宽度明显小于其他属性获得的界面宽度。在此基础上，依据“10% ～90%”原则计算界面宽度，发现以序参数为标准，界面宽度同样存在非常一致的各向异性。且采用不同的序参数（aq6和ξ）得到的界面宽度不同，用aq6标定的界面宽度始终大于用ξ标定的界面宽度。这也是目前界面区定位的最大问题。