多层地质与热渗耦合环境下U型地埋管换热性能研究

张顺飞

重庆交通大学土木工程学院

0 引言

地源热泵概念最早出现在1921年，由H.Zoelly[1]学者在一份专利文献中首次提出，将土壤源作为热泵系统地温热源的概念。地埋管地源热泵因节能环保被广泛关注，核心设备地埋管换热器的地下换热过程是较复杂的非稳态传热过程。直到20世纪的30年代至40年代，热泵的研制和开发才相继在英国、美国等国展开。1946年美国第一个地源热泵系统在俄勒冈州的波特兰市中心区安装使用[2]，逐渐引起人们的关注，提出了关于土壤源热泵系统的许多基础性理论及相关数学模型[10]进行相应的研究，同时进行了相关实验，获得了必要的实验测试数据，为以后的研究奠定了实验研究基础。

於仲义[3]分析了不同的地埋管结构与尺寸、土壤的热物性、分层特性、换热负荷特性以及不同运行方式下的地埋管传热特性，并针对土壤分层特性提出了区段换热理论及动态迁移特性，从而为地埋管换热器的优化设计及空调系统参数匹配提供了理论依据。Jinzhong Hu[4]研究并提出地下水流速对钻孔周围土壤温度的影响，结果表明，由于地下水平流引起平面温度场变形，当等效流速达到一定数量级时，地下水流速能有效缓解热(冷)积累，且地下水流速越高，温度场越快达到稳定。工程中如果忽略渗流这一因素，将导致系统实际运行效果与设计工况有所偏差。

本文以重庆某实际工程地质环境为依托，以单U型地埋管的出口水温、单位井深换热量、钻孔壁过余温度为衡量指标，探讨有(无)地下水渗流环境下、系统运行间歇比对U型地埋管换热性能的影响，为地源热泵系统的设计与运维提供一定的参考。

1 工程概况

本研究以重庆市某可再生能源建筑地源热泵系统为例，分析地埋管换热器在热渗耦合与土壤分层工况下的轴向换热性能，其换热场区以换热性能良好的砂岩、泥岩为主。表1为地质勘测结果。

2 物理模型和数值模拟方法

2.1 建立单U形地埋管换热器三维非稳态分层传热模型

由于U型地埋管的几何形状及管内流体与土壤间耦合传热过程的复杂性，对模型进行以下假设和简化：

1)忽略地表大气与土壤间的换热，假设地表面为绝热边界条件；

2)假设土壤中的渗流是水平方向，不考虑纵向的渗流；

3)忽略回填材料与地埋管的管壁、周围岩土体之间的接触热阻，设回填材料与地埋管的管壁以及周围岩土体之间接触良好；

4)忽略U型管底部弯管段与周围的传热，未假设弯管段外壁面和底部为绝热边界条件；

表1 岩土层热物性参数

5)假设岩土体沿轴向热物性差异的多孔介质，各层岩土体之间的导热系数、比热容、热扩散率等参数保持均匀不变，岩土体初始温度相同。

2.2 多孔介质中流体流动传热控制方程

实际情况下地下水通常分布不均，存在于多孔介质中[5]，岩土体中会存在含湿岩土层，甚至含水层，且沿着深度方向岩土体很可能有明显的分层现象，不同地质层的导热性能有可能差异很大。对于多孔介质内渗流，流动为不可压缩流体的层流运动，不考虑源项时，主要的控制方程有连续性方程、动量方程和能量方程，见式（1）-（3）：

连续性方程

动量方程

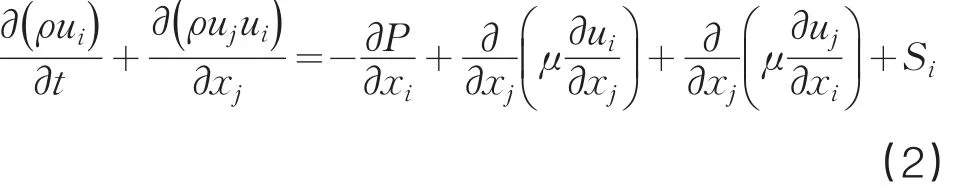
能量方程

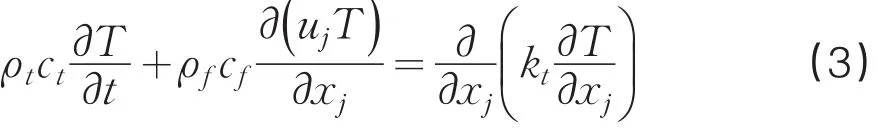
式中，φ为多孔介质孔隙率，Si是Fluent多孔介质模型在标准动量方程中附加的动量源项，ρtct和kt分别为多孔介质总热容和总导热系数，Si、ρtct和kt可根据式（4）-（6）确定：

α—渗透系数；

ρf cf—多孔介质中液相的热容

kf—导热系数；

ρscfs—多孔介质中固相的热容

ks—导热系数

J.Pascal指出：当地下水渗流速度较小时，惯性损失项可忽略不计，即C 2为0，附加的动量源项仅考虑粘性损失项。

2.3 初始条件

冬、夏季制热/冷工况：系统初始时，地埋管与回填材料、土壤处于平衡状态，即管内流体、管壁、回填材料和土壤的温度均为初始温度293K，渗流层为2、3、4层，渗流速度为5×10-6m/s。

2.4 几何建模与网格划分

采用Gambit软件进行几何建模及网格划分，如图1所示。模型几何参数参照重庆某可再生能源建筑地源热泵系统中竖直单U形地埋管换热器系统的几何尺寸，见表2。为使模型与实际工程更为接近，将U形管按实际构造进行分层，在模拟过程中，将岩土体分为六层，每层岩土体的热物性参数按表1设置。

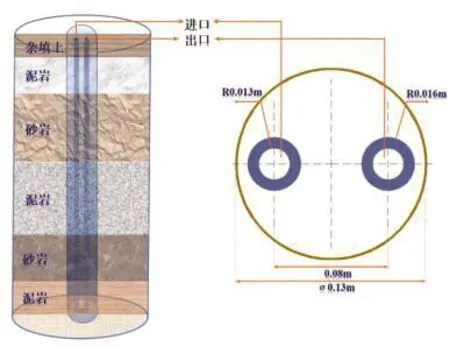
图1 岩土体分层模型及钻孔示意图

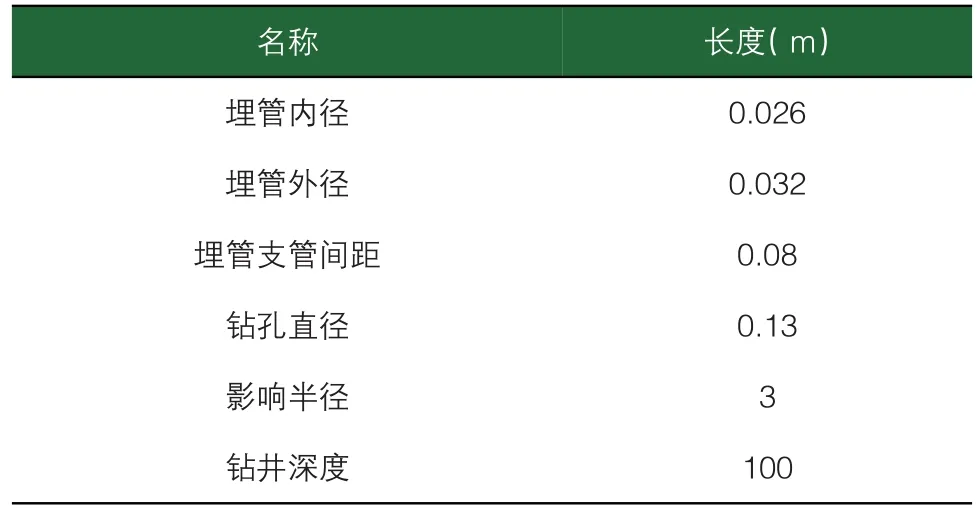
表2 竖直单U型地埋管换热器模型的几何参数

各部分网格划分（依次为U型管底部、钻孔、岩土体），见图2。

图2 各部分网格划分（依次为U型管底部、钻孔、岩土体）

3 模拟结果及分析

3.1 渗流模型与纯导热模型换热对比研究

3.1.1 单位井深换热量

由图3可知，纯导热模型和热渗耦合模型的出口水温均随时间逐渐升高，运行至第七天，纯导热模型和热渗耦合模型的出口温度相差0.36 K。由此可见，热渗耦合模型的出水温度在第2天结束时已几乎稳定，而纯导热模型的出口水温至第七天结束仍有上升趋势，说明地下水渗流能加速地埋管流体出口水温达到稳定。两者的单位井深换热量均随时间逐渐下降，运行至第七天结束，热渗耦合模型的单位井深换热量比纯导热模型提高了10.74%。

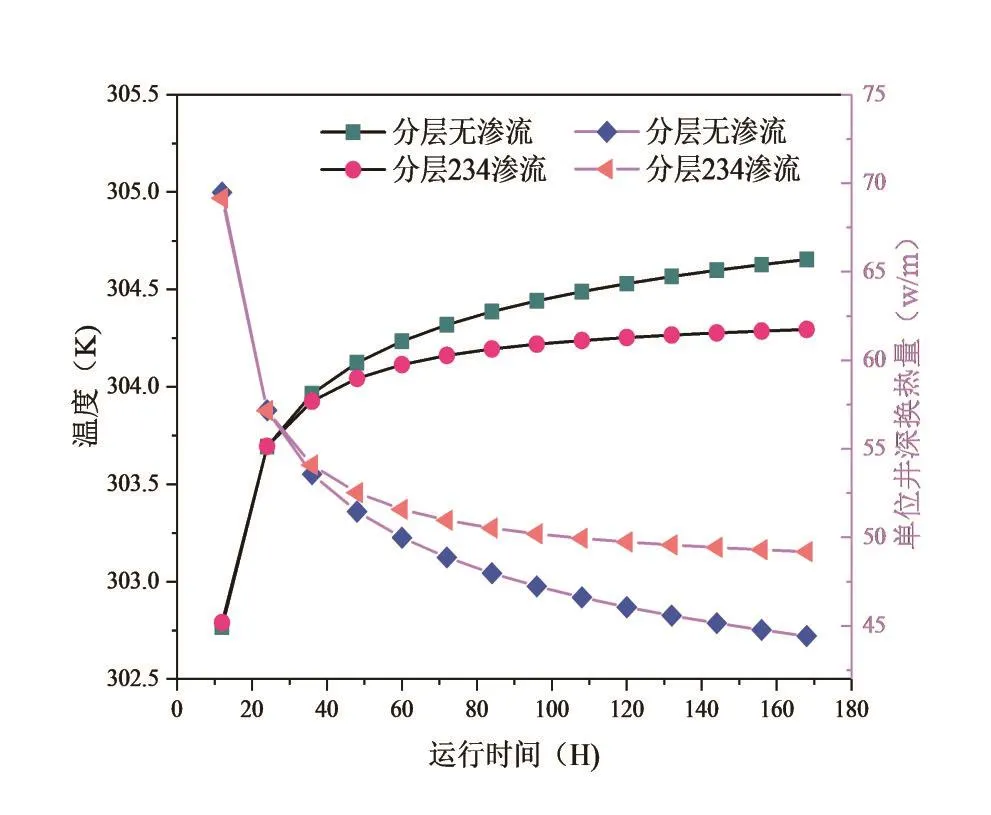
图3 出口水温及单位井深换热量随时间的变化

3.1.2 沿钻孔壁轴向温度分布

图4为运行7天后距钻孔中心x=0.065 m处沿程钻孔壁的轴向温度分布。热渗耦合模型中钻孔壁的过热温度在各深度下都低于纯导热模型，各地层中最大温差分别为0.287 K、0.906 K、0.789 K、0.856 K、0.148 K、0.161 K。结果表明，当存在地下水渗流时，钻孔壁过余温度曲线具有明显的差异，渗流作用下的第2、3、4层的孔壁过余温度比纯导热模型分别下降9.36%、8.82%和8.48%，可见地下水可以降低地埋管周围土壤的温度，使其有更高的换热量。

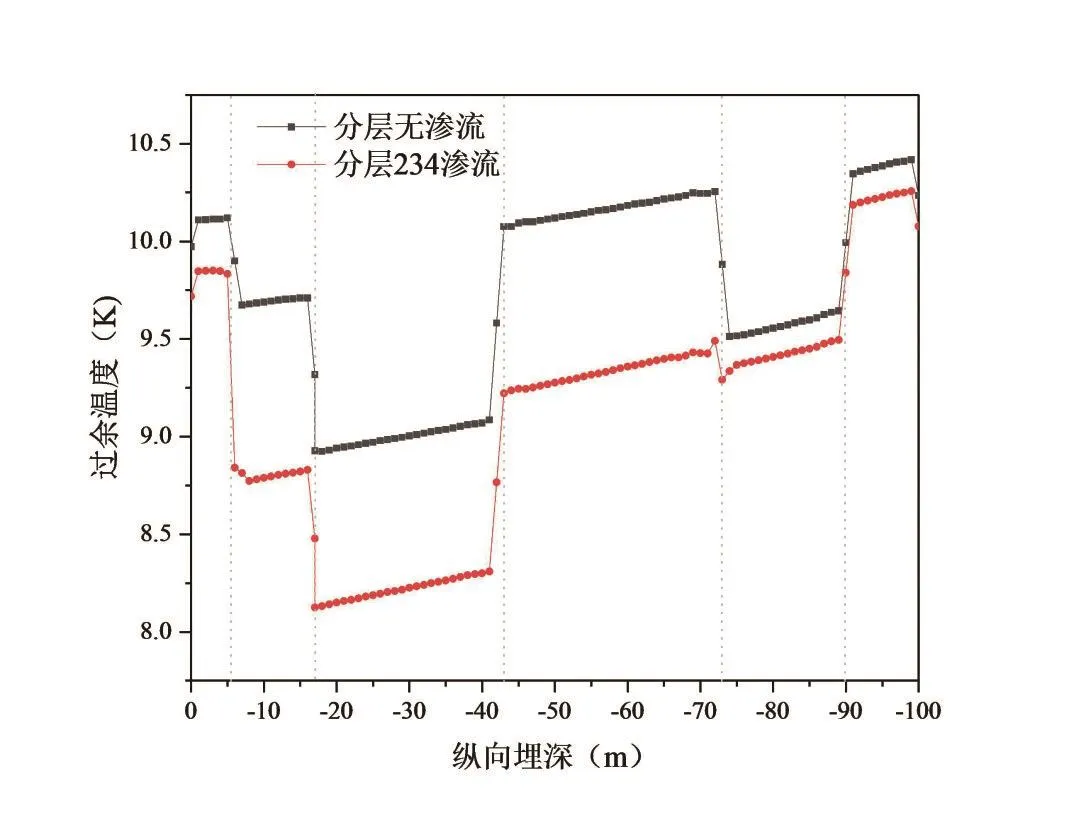
图4 钻孔壁轴向温度分布

3.1.3 温度轮廓线

图5分别给出了纯导热模型和热渗耦合模型在运行七天后的土壤轴向温度云图。由图5可见，由于地下水的渗流作用，地埋管周围土壤温度场不再对称，而是沿着渗流方向发生了偏移。地下水渗流能明显减少垂直与渗流方向的热影响距离，而地下水渗流的影响导致下游的热作用区域增大，而上游的热作用区域缩小。沿着渗流方向下游的土壤热作用距离远大于纯导热模型，且土壤的热扩散系数越大，热影响距离越小，如第二层和第四层的泥岩热影响距离大于第三层的砂岩。由于热量会随着渗流的流动在短时间内迁移到沿着地下水流的下游，而随着时间的推移，渗流作用下热量会较快地被带到更远处。其原因在于砂岩的导热系数和热扩散系数均高于泥岩，除了垂直于渗流方向的径向距离较纯导热模型降低以外，砂岩层热扩散系数大的特点同样影响着沿着渗流方向的径向距离。即：地下水渗流对与其逆向的传热有抑制作用，而对沿着渗流方向的传热有促进作用。因此有无渗流对埋管周围土壤温度分布有很大的差别。

由此可见，在多层地质中，地下水的渗流是埋管换热性能不可忽略的一部分，如何利用地下水渗流在多层地质中的应用，对埋管的设计、造价、节能运行都起着举足轻重的作用。此外，在对管群进行设计时，可以减小垂直于渗流方向的间距，适当沿着渗流方向的间距。

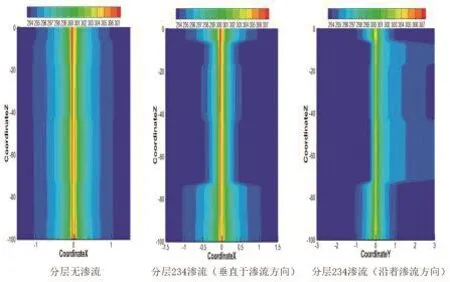
图5 轴向温度云图

3.2 间歇运行对埋管换热性能的对比

3.2.1 单位井深换热量

暖通空调系统的运行管理对建筑节能的意义重大，一般情况下，地埋管与土壤间的热交换根据建筑空调需要多为间歇且有周期性。在分层热渗耦合模型中对比分析三种不同运停比对埋管换热性能的影响。

在分层热渗耦合模型中，选取第2、3、4层为渗流层，渗流速度为5×10-6m/s，模拟运停比为8∶16、10∶14、12∶12三种情况下，间歇运行对埋管换热性能的影响。

由图6可知，间歇运行对埋管的单位井深换热量具有明显的提升，随着运停比的增大，单位井深换热量逐渐减小，运停比为8∶16的单位井深换热量比运停比为12∶12的单位井深换热量增加2.5%，比连续运行的单位井深换热量增加11.9%，由此可见，在实际地源热泵的运行过程中，系统的运行对埋管的换热性能具有不可忽略的影响。

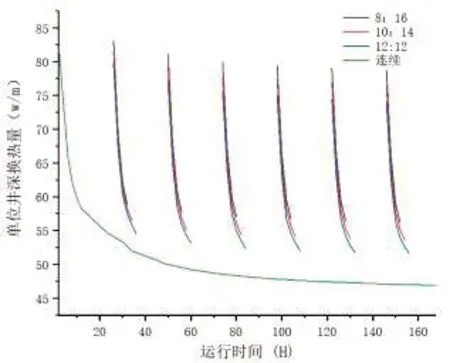
图6 间歇运行状态下单位井深换热量随时间的变化

3.2.2 间歇和连续散热对钻孔壁的动态温度响应

地下水渗流速度为5×10-6m/s时，钻孔壁在不同运停比和连续运行情况下土壤中x=0.065 m，y=0 m，z=30 m处的动态温度响应曲线见图7。

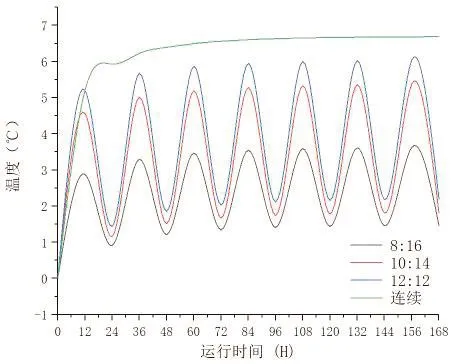
图7 动态温度响应

由图7可见，间歇散热时土壤温度总体也随着时间的推移而升高，但每个间歇时段内土壤温度都有一定的恢复。运行7天后，连续运行在（0.065，0，-30）处的温度升高了6.19℃，而间歇运停比为8:16、10:14、12:12在（0.065，0，-30）处的温度分别仅升高1.47℃、1.82℃、2.2℃，表明间歇运行有利于地温恢复而使土壤升温速率减缓。而且，运停比越小，间歇时段土壤温度的恢复最低。运停比为12∶12时比运停比为8∶16在第7天土壤温度恢复后高49.7%，由此可见，当建筑负荷有不同需求时，如不考虑埋管间歇散热所引起的土壤温度响应和恢复特性的影响，则关于埋管换热能力的设计计算就会产生很大的偏差。

4 结论

热渗耦合模型的出口水温总是低于纯导热模型，连续运行7天后，热渗耦合模型的单位井深换热量比纯导热模型提高了10.74%，地下水渗流使分层模型中第2、3、4层的换热比重较纯导热模型分别提高了0.8%、0.5%和2.5%；在存在地下水渗流时，钻孔壁过余温度曲线具有明显的差异，渗流作用下的第2、3、4层的孔壁过余温度比纯导热模型分别降低9.36%、8.82%和8.48%，可见地下水可以降低地埋管周围土壤的温度，使其有更高的换热量。

间歇运行工况下，随着运停比的增大，单位井深换热量逐渐减小，运停比为8∶16的单位井深换热量比运停比为12∶12的单位井深换热量增加2.5%，比连续运行的单位井深换热量增加11.9%，运停比为12∶12比运停比为8∶16在第7天土壤温度恢复程度高49.7%。由此可见，在实际地源热泵的运行过程中，系统的运行对埋管的换热性能具有不可忽略的影响。