基于果蝇算法的物联网节点定位技术研究

郭 悦,王红军,解梦奇

(国防科技大学 电子对抗学院,合肥 230037)

0 概述

近年来,随着智慧城市、云计算、大数据等概念的相继提出,物联网产业进入到快速发展的阶段。物联网在当前应用比较广泛的领域有智能路灯、物流和共享单车等方面,特别是在未来5G网络架构中,专门设计了mMTC大规模物联网业务。基于位置的服务(Location-based Services,LBS)是物联网范围内最具前景的应用之一,基于物联网的大多数公共服务和商业应用均依赖于节点的位置信息,约70%的物联网应用开发直接依赖或受益于节点位置信息的获取[1],精确的节点定位在物联网位置服务应用中占有越来越重要的地位。许多相关的数据只有在确定节点的确切位置信息时才有意义,否则毫无价值。物联网中的位置信息不仅影响了人们生活的方方面面,而且已经扩展和应用到军事领域。

物联网中节点的定位[2-4],即通过已知节点的信息来对未知节点进行定位,是解决特定环境中实体定位问题(如环境监测和入侵定位)的关键技术。已知节点即测量节点,是用来对未知节点进行定位的设备,可以通过测量节点配备的GPS系统获得测量节点准确的位置信息,未知节点即为需要定位的目标节点。由于一定的环境因素或者其他条件的制约,无法通过GPS系统获取目标节点的位置信息,则需要一些其他的定位方法。传统的定位方法包括基于测距的以及非测距的定位方法,基于测距的定位方法有极大似然估计法(Maximum Likelihood Estimation,MLE)、三边测量法和最小二乘估计法(Least Squares Estimation,LSE)等;基于非测距的定位方法包括APIT(Approximate Point-in-triangulation Test)算法、边界盒(Bounding-Box)算法和DV-Hop算法等。其中边界盒算法[5]是一种分布式定位的经典算法,该算法通过矩形区域对测量节点的通信范围进行约束,其具有计算简单、操作容易的优点,但定位误差较大。为平衡算法的动态性能与定位准确度,本文提出一种融合边界盒算法与果蝇优化算法(Fruit Fly Optimization Algorithm,FOA)的改进算法,该算法利用边界盒算法来约束FOA算法的初始搜索范围,同时通过增加权重系数重构算法的味道浓度函数,以改善算法的定位性能。

1 相关研究

近年来,随着群智能算法的不断发展,其在解决复杂问题方面为人们提供了有力的工具,同时对于定位问题的处理也具有良好的效果。粒子群优化(Particle Swarm Optimization,PSO)算法被用来解决节点定位的问题,在粒子的搜索空间中,通过并行的方式进行迭代以实现优化[6]。为获得更高的定位精度,文献[7]使用经典的蚁群算法来优化三边测量算法的误差函数,然而,该算法具有计算速度较慢、易陷入局部最优的缺陷,很大程度上影响了算法的定位精度。果蝇优化算法[8-10]是一种较新的群智能优化算法,相比于其他群智能算法,具有易于实现、结构简单、原理易懂等优点。

由于果蝇优化算法可用来处理优化问题,在较短时间被成功地应用于网络能效优化、物流[11]、规划问题[12-13]、控制辨识问题[14-15]等方面。近年来,该算法被应用于物联网中节点的定位,且取得了较好的效果。文献[16]基于果蝇优化算法提出一种新型的节点定位算法,将m个测量节点对未知节点进行定位之后的平均误差表达式作为算法的味道浓度函数,通过迭代实现优化,不断缩小未知节点与测量节点之间的距离误差,最终来确定未知节点的位置坐标。该方法在一定程度上解决了一些传统算法定位不精确的问题。但是在搜索过程中,每个粒子的轨迹取决于味道浓度最佳个体的位置,当没有更好的个体更新种群的最佳位置时,所有的粒子都会迅速聚集在当前最佳位置的区域,导致早熟问题。同时在客观上由于测距误差的存在且误差函数区分度小,使得定位误差增大。文献[17]提出一种改进的果蝇优化算法DFOA(Dynamic Step Fruit Fly Optimization Algorithm),基于惩罚函数的思想,对算法的味道浓度函数进行优化,并采用误差修正系数μ滤除掉一些具有较大测距误差的距离,使用惩罚系数M加大对非可行点的惩罚,并且在误差修正参数μ的基础上添加约束，以进一步减小未知节点的可行域范围。但是惩罚系数M多凭经验选取,其选取不当会对测量结果造成较大误差。

通过分析不难发现,在对果蝇优化算法进行初始化时,需要在搜索空间中随机初始化许多果蝇个体,当果蝇种群在较大的空间进行搜索时,算法的收敛速度逐渐变慢,同时定位精度也会有一定程度的下降。

2 定位算法

2.1 边界盒算法

边界盒算法自从被提出以来,已广泛应用于物联网中未知节点的定位,它是一种基于非测距的定位方法。该方法使用矩形区域来约束定位时未知节点所在的区域范围,测量节点通信范围如图1所示。

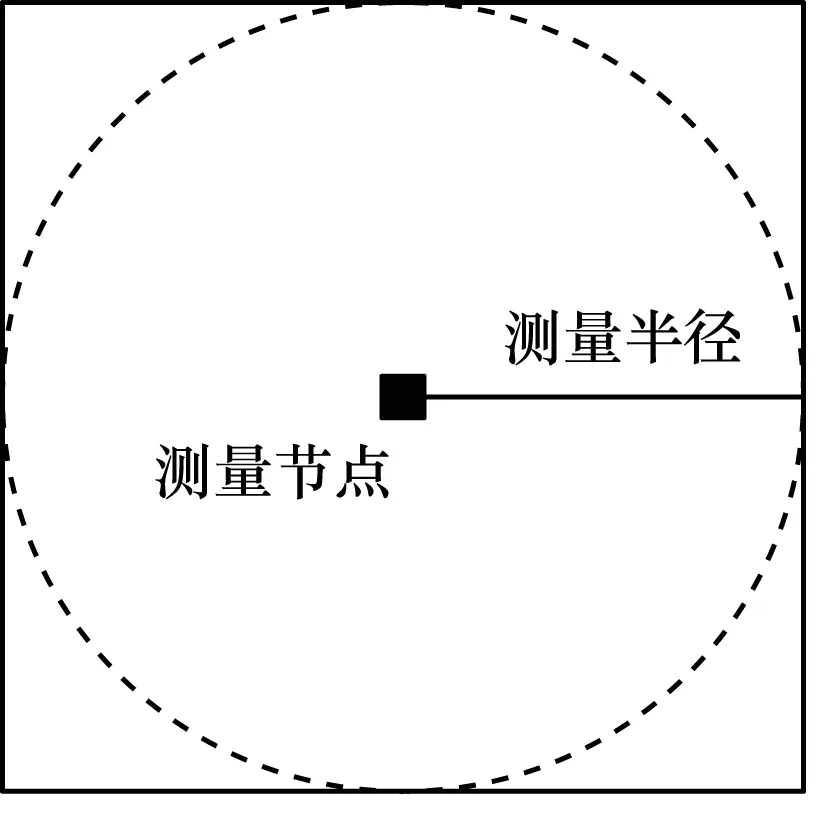
图1 节点通信范围

如果未知节点与测量节点间的距离小于测量节点的通信半径,则测量节点可以接收未知节点发射的信号;未知节点如果在测量节点通信半径所覆盖的通信圆区域内,那么它一定处于以测量节点为中心,以2倍通信半径作为边长的正方形区域内。所以,矩形相互重叠的区域可以用作未知节点位置所在的估计区域。

如图2所示,待定位的未知节点处于测量节点A的通信矩形A1A2A3A4内,同时也位于测量节点B的通信矩形B1B2B3B4范围内,则未知节点一定处于2个矩形相交部分B1C1A3C2的范围内。因此,矩形相互重叠区域的中心可以用作对未知节点进行定位的结果。如果直接用通信圆的交集作为定位区域,则计算量太大,该算法将矩形区域交集的中心作为定位结果,复杂度和计算量小、操作简单,但定位精度相对偏低。

图2 边界盒算法示意图

2.2 果蝇优化算法

果蝇优化算法是一种新的全局搜索优化方法,通过模拟生物学中果蝇独特的觅食行为,基于果蝇个体优越的嗅觉和视觉搜索机制,在搜索空间中进行迭代寻优来达到优化的目的。

本文将果蝇优化算法应用于物联网中节点的定位,通过一步步地迭代实现优化,最终得到未知节点的坐标。经过研究发现,当对果蝇个体进行初始化时,在搜索空间中需要随机初始化许多的果蝇个体,文献[16]在迭代次数、种群规模及飞行区间相同的条件下,分别在[0,30]及[0,5]范围内初始化果蝇位置。仿真结果表明,在其他条件相同的情况下,[0,5]范围内算法的收敛速度较快,且容易找出果蝇的最终聚集位置,定位精度较高。当搜索空间较大时,算法的收敛速度较慢,定位精度也会有所降低。因此,可以优化果蝇种群的初始搜索空间,以满足定位要求。

为得到更好的定位性能,本文提出BFOA定位算法。该算法的主要思想是通过边界盒算法将果蝇算法的初始搜索范围约束在一定范围内,再应用FOA定位算法得到目标节点的最优估计位置。

在文献[16]中,未知节点与m个已知节点的距离误差函数被用作果蝇算法的味道浓度判定函数,如式(1)所示。

(1)

其中,di为目标距离。

通过迭代寻找味道浓度函数最小值作为果蝇的最优位置,即待定位节点的位置,通过此方法在一定程度上提高了定位精度。然而,在测距过程中可能存在某些估计距离与实际距离有较大偏差,导致定位结果产生误差。本文采用基于RSSI[18-19]模型的测距方法,根据在自由空间中无线电波的传播规律可知,在距离测量的过程中,2个节点之间的距离越近,测得的距离误差越小;距离越远,误差越大。因此,本文算法重新配置测距值集合中各测距值的权重,将由RSSI测距得到的距离值转换成算法的权值,文中的权重系数wi用于对在味道浓度函数中测距值所占的比重进行约束。

(2)

误差函数为:

(3)

改进后的味道浓度函数为:

(4)

BFOA算法流程如图3所示。

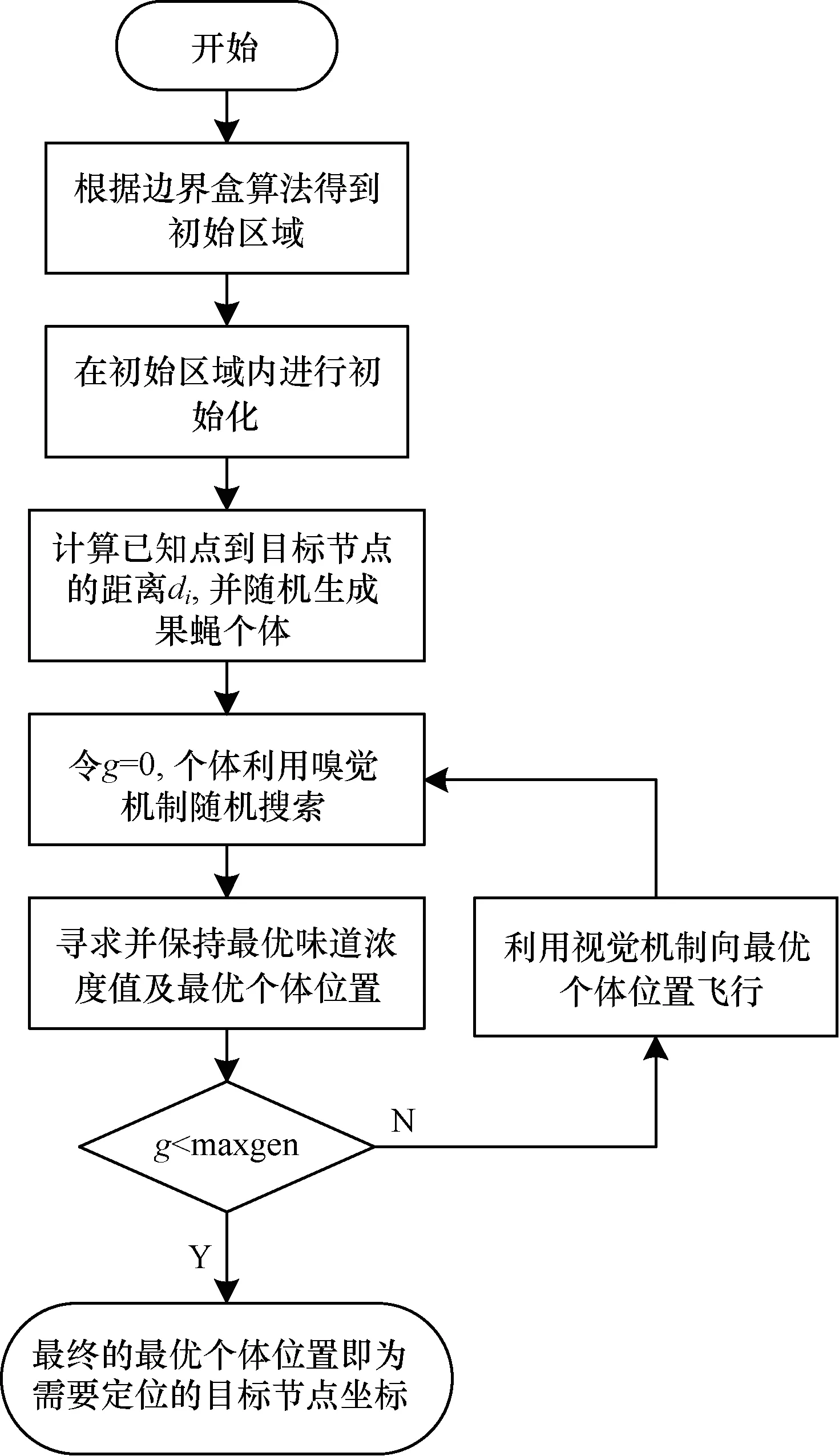
图3 BFOA算法流程

BFOA算法的具体步骤为:

步骤1使用边界盒定位算法对果蝇优化算法的初始搜索空间进行优化。

步骤2对果蝇优化算法的相关参数进行初始化,包括最大迭代次数(maxgen)和种群规模(sizePop)等。

步骤3测量节点通过 RSSI测距技术测量到目标的距离di,在步骤1得到的区域内随机生成第一批果蝇个体。

步骤4选择具有最佳味道浓度的个体作为果蝇优化算法初始的种群位置,并保留最佳浓度值处的坐标值。

步骤5根据视觉搜索机制产生果蝇个体,并通过式(4)来计算果蝇个体的味道浓度值用于迭代寻优。

步骤6确定是否满足收敛条件,如果满足,则输出最后一次迭代的坐标作为估计位置;若不满足,则继续执行步骤4～步骤5。

3 实验与结果分析

为了更好地评估本文提出的BFOA算法的性能,利用Matlab R2016a进行仿真实验,以一个节点定位的过程为例:场景为在100 m×100 m的二维矩形区域范围内设置一个未知节点,其坐标为(40,50);粒子群算法的参数设置为:wstart=0.9,wend=0.4,w=wend×(wstart/wend)(i+1)/mmaxgen,其中wstart和wend分别为初始和结束时算法的惯性权重;参照文献[18],DFOA算法的惩罚系数M设为8。

假设每次仿真时具有相同的网络环境，实验数据取运行1 000次的平均定位误差值作为本次的实验结果。为了衡量算法定位精度，选用式(5)的计算结果作为算法的评价标准。

(5)

其中,(x,y)表示最终算法的定位结果,(xreal,yreal)表示需要定位的节点的真实坐标。可见,算法定位的平均误差值越小,则定位精度越高。为了验证算法的定位效果,分别比较粒子群算法、文献[16]提出的基于果蝇优化算法的节点定位方法、DFOA算法与本文提出的BFOA算法随测量节点数量和种群规模变化时的定位精度,并且对4种算法的收敛速度、定位精度以及稳定性进行分析。

3.1 测量节点数量对定位效果的影响

为了说明不同测量节点的数量对定位精度的影响,实验时将种群规模设置为20,最大迭代次数设置为100。在测量节点数目不断增加的情况下,比较粒子群算法、果蝇优化算法、DFOA算法与本文提出的BFOA算法的定位精度。若4种算法的平均定位误差比较接近,则说明测量节点数量的变化对定位结果影响不大;若平均定位误差具有较大的差距,则说明定位效果差距较大,所得的仿真结果如图4所示。

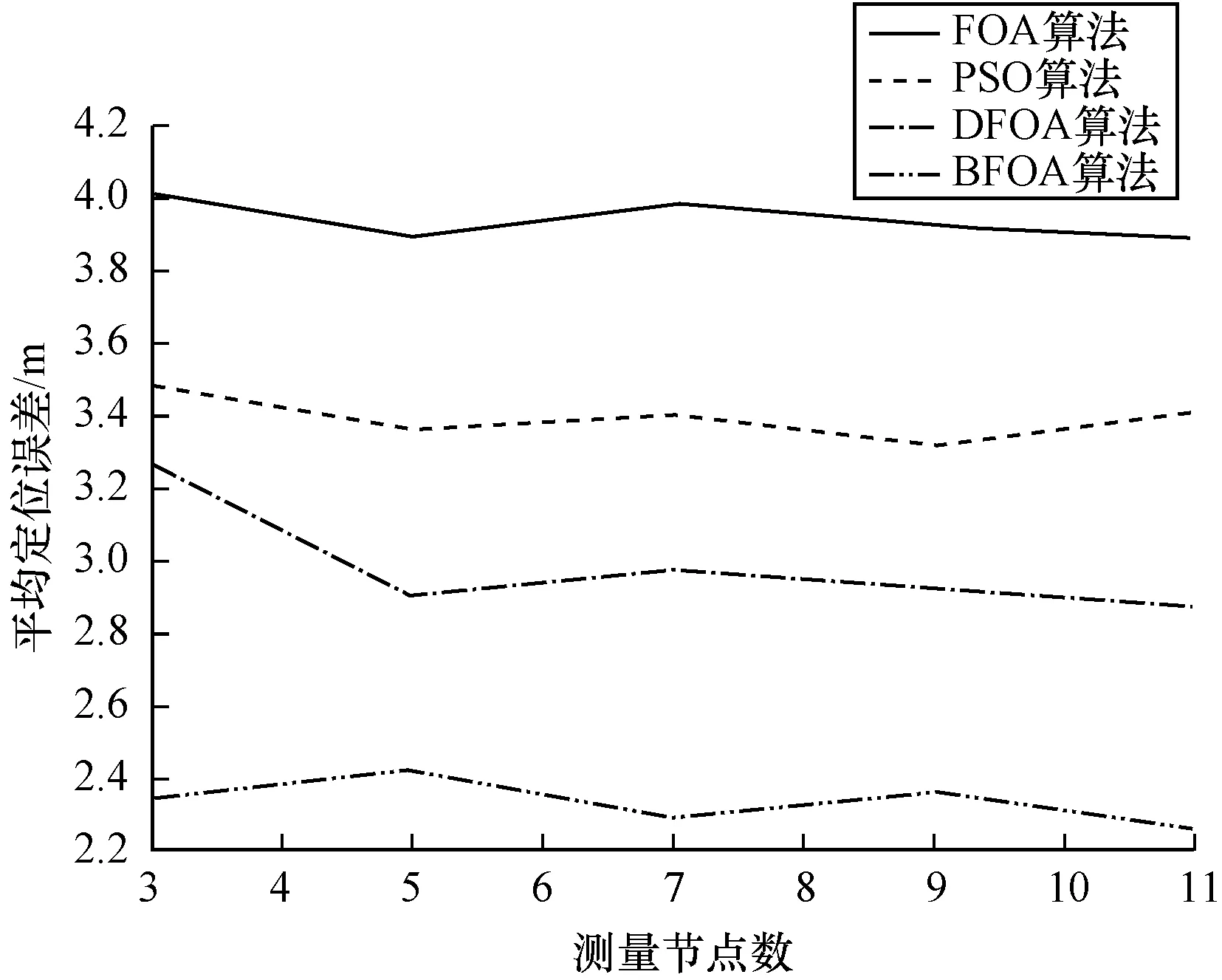
图4 测量节点数量对定位效果的影响

Fig.4Effect of the number of measurment nodes on localization

从图4可以看出,当测量节点数由3个增加到11个时,实验得到的粒子群算法、果蝇优化算法、DFOA算法以及BFOA算法的平均定位误差分别处于(3.312 6 m,3.481 5 m)、(3.886 5 m,4.023 8 m)、(2.864 2 m,3.261 4 m)和(2.265 3 m,2.419 5 m)的区间中,可以看出测量节点数量的增加对定位效果的影响不大。综上所述,从节约能源以及硬件设备的复杂性等方面考虑,选取的测量节点越少越好,本文中采取3个测量节点进行定位。

3.2 种群规模对定位效果的影响

为验证算法的动态性能,在仿真时考虑了种群规模这个指标。通过交叉定位,将测量节点的数量设为3个,最大迭代次数设为100,并不断改变种群规模。在种群规模增加的情况下,分别比较粒子群算法、FOA算法、DFOA算法以及本文提出的BFOA算法的定位效果,所得的仿真结果如图5所示。

图5 不同种群规模的定位效果

从图5可以看出,当果蝇种群规模增加时,4种算法的定位精度也随之增加,同时当具有较大的种群规模时,4种算法的定位效果均趋于稳定。然而,当种群大小增加时,算法的动态性能将会随着计算量的增加而降低。当种群规模达到20之后,4种算法的定位精度不会显著增加,相比于FOA算法、PSO算法以及DFOA算法,BFOA算法的定位精度较高。所以,为了平衡算法的动态性能与定位的准确性,定位时将种群规模设为20。

3.3 BFOA算法收敛性能和定位精度分析

由3.1节和3.2节内容可知,将种群规模设为20,测量节点数量同样设为3个,最大迭代次数设为100。在迭代次数不断增加的情况下,比较粒子群算法、FOA算法、DFOA算法与本文提出的BFOA算法的收敛性能和定位精度,仿真结果如图6所示。

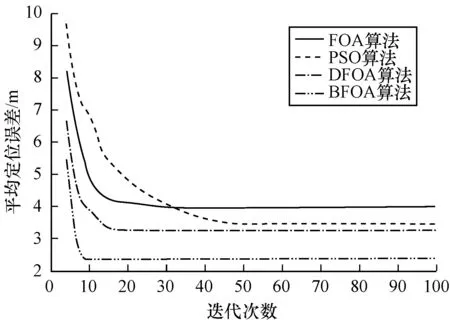
图6 迭代次数增加时4种算法定位效果对比

Fig.6 Comparison of localization effects of 4 algorithms with increasing iterations

从图6可以看出,BFOA算法在迭代次数大于8次、DFOA算法在迭代次数大于15次、FOA算法在迭代次数大于18次、PSO算法在迭代次数大于45次后定位性能均趋于稳定,但BFOA算法的收敛速度明显较快。此外,随着迭代次数的增加,4种算法定位精度均同步提高,从变化趋势中可以看出,DFOA算法的定位精度明显优于FOA和PSO算法,在迭代30次之后PSO算法比FOA算法定位精度要高。但相比FOA、 PSO与DFOA算法,BFOA算法具有更低的定位误差,即具有更高的定位精度。

综合考虑算法的收敛速度和定位精度,BFOA算法的定位性能优于DFOA、PSO和FOA算法。

3.4 BFOA算法稳定性分析

在种群规模设为20,测量节点数量设为3个,最大迭代次数设为100的条件下,比较粒子群算法、FOA算法、DFOA算法与本文提出的BFOA算法的稳定性。4种算法均进行了20组仿真对比实验,每组仿真实验中4种算法均运行1 000次,取与4种算法相对应的1 000次实验的平均定位误差值作为本组的实验结果,即通过比较4种算法多组实验的平均误差值波动情况来验证算法的稳定性,所得仿真结果如图7所示。

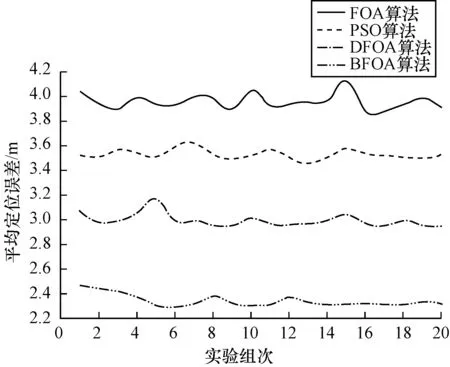
图7 4种算法在不同实验组次下的定位效果

Fig.7 Localization effects of 4 algorithms in different experimental groups

从图7可以看出,BFOA算法定位的平均误差波动最小,算法的稳定性相对最好,FOA算法定位的平均误差波动较大,算法的稳定性差，本文提出的算法具有很高的定位精度,同时具有更好的稳定性。果蝇优化算法迭代中的搜索效率与果蝇个体所处位置和迭代次数有关,但并不与迭代次数呈严格的线性关系。本文采用边界盒算法对初始搜索空间进行优化使得搜索效率更高,稳定性增强。因此,在算法的稳定性方面,BFOA算法优于DFOA、PSO和FOA算法。

4 结束语

本文提出一种基于果蝇优化算法的物联网节点定位方法,通过采用边界盒定位算法优化果蝇种群的初始搜索范围,同时重构算法的味道浓度函数以提高算法的定位性能,通过仿真实验比较测量节点数量与种群规模大小对4种算法定位效果的影响，结果表明,与FOA、PSO和DFOA定位算法相比,本文算法在定位精度和收敛速度方面都有所提高,同时具有更高的稳定性,且算法的复杂度较低。下一步将继续对定位应用进行研究,并在实际环境中验证BFOA定位算法的有效性。