光纤周界报警信号自适应压缩感知

杨正理，史 文，陈海霞

(三江学院 机械与电气工程学院，南京 210012)

引 言

分布式光纤周界报警系统以其检测灵敏性高、不受电磁干扰等优点被广泛地应用于一些重要领域，通过对光纤振动信号进行分析与辨识来判断是否存在蓄意入侵[1]。然而，光纤振动信号是一种复杂的非平稳信号，频率高，当采用传统的奈奎斯特全采样方法进行信号传输与处理时，必然存在网络宽带、存储容量、计算速率等一系列限制问题。

信号的压缩感知(compressed sensing，CS)方法[2-3]为解决这一问题提供了良好方案。近年来，诸多学者在采用压缩感知方法处理图像和各类复杂信号方面进行了广泛研究，并取得了较大成果。参考文献[4]中提出了一种基于小波理论和压缩感知算法建立多字典的遥感图像超分辨算法，采用K奇异值分解方法构建反映图像特征的过完备字典对图像进行稀疏表示，提高了图像的主观视觉效果，并从客观上提高了图像的峰值信噪比(peak signal-to-noise ratio，PSNR)及重构速度。参考文献[5]中提出了一种自适应机械振动信号分块压缩感知算法，通过构造与信号矩阵相适应的冗余字典，并按照不同机械信号块在冗余字典下的匹配追踪系数的衰减速度定义出不同的复杂度权值，构造出信号压缩感知的自适应采样策略，使信号重构的精度得到提高。参考文献[6] 中提出了一种利用贝叶斯算法对复合材料的冲击载荷历程进行压缩感知，将冲击响应的动力学表示为单位脉冲响应函数和冲击载荷的卷积，从而获得基函数的最优稀疏系数，并用实验验证了所提出方法的有效性和可行性。参考文献[7]中利用多通道脑电信号的时空特征构建出非正交的过完备学习字典，对信号进行稀疏表示，提高了信号的重构性能和算法的计算速度。参考文献[8] 中采用小波变换对语音信号进行级数分解，并对小波系数进行自适应稀疏变换，提高了信号在频域的稀疏度，与直接采用压缩感知的方法相比，该方法使语音信号的压缩率提高了一倍。参考文献[9]中采用离散余弦变换对电能质量扰动信号进行稀疏变换，提出一种避免频谱泄露的改进重构算法，并在此基础上提出频谱能量差的概念，有效地避免了过度估计信号稀疏度，提高了算法的运算速度。

然而，目前针对光纤振动信号压缩感知的研究还很少，且压缩感知算法在图像、语音及其它复杂信号中的应用也存在着一些不足：(1)传统的稀疏变换方法，例如离散余弦变换、离散小波变换等对信号的变换不够彻底，由此使信号在其稀疏域的稀疏度不高，还可能丢失一些有用的信号特征信息；(2)利用小波变换对信号进行稀疏分解的过程中，当采用固定阈值处理小波系数时，要么会使信号稀疏度过低、压缩率不足；要么会使信号稀疏过度、丢失有用信息，信号的重构精度降低；(3)传统的压缩感知方法得到的观测数据较多，需要较高的网络传输带宽。

针对上述不足，本文中提出了一种基于小波包变换的光纤振动信号自适应压缩感知方法。首先，采用小波包变换对光纤振动信号进行多尺度分解，对仍含有丰富信息的高频部分也进行分解，进一步提高了信号在频域的稀疏度，并最大限度地保留了信号的特征信息；然后，计算各尺度小波包系数高频部分的数学期望，作为各尺度阈值对本尺度下的小波包系数进行置零处理，自适应地选择最优分解尺度，以获得较高的频域稀疏度；最后，通过自适应级小波包系数块的数学期望和信息熵对系数块进行分类，并对不同类型的系数块采用不同的信息处理方法，减少了观测数据量，降低了信号的传输带宽。

1 基于小波包变换的信号稀疏表示

1.1 小波包变换

与小波变换相比，小波包变换为信号提供了更精细的分析方法。对仍含有丰富信息特征的高频信号也进行分解，并能根据信号的具体特征自适应地选择频带来提高高频信号的分辨率。以信号的3层小波包分解为例来分析其分解过程，如图1所示。

Fig.1 Tree of three-layer wavelet packet decomposition

图1中，用L和H分别表示小波分解后的低频和高频部分，则原始信号S0经第1层小波包分解后得到低频信号S1,L和高频信号S1,H；对S1,L再进行一层小波包分解后得到下一尺度的低频信号S2,LL和高频信号S2,HL，对S1,H进行一层小波包分解后得到下一尺度的低频信号S2,LH和高频信号S2,HH；对低频部分S2,LL进行第3层分解后的低频S3,LL和高频S3,HLL部分……。依次类推，可以得到N层小波包分解的低频信号和高频信号。假设正交尺度函数、正交小波函数分别为φ(t),φ(t)，则小波包变换的双尺度方程[10]可表示为：

(1)

式中，t为时间参量；k为平移参量；h(k),g(k)分别为多尺度分析中低、高通滤波器系数，且g(k)=(-1)k×h(1-k)，即两系数具有正交性。

为进一步推广，由(1)式得到下列递推关系：

(2)

式中，当n=0时，递归函数ω0(t)退化为尺度函数φ(t)，ω1(t)退化为小波函数φ(t)，即ω0(t)=φ(t)，ω1(t)=φ(t)。所以，(2)式所表示的函数集合{ωn(t)}(n=0,1,…,n)可以看成是基于ω0(t)=φ(t)所确定的小波包。或者说，小波包就是一个包括φ(t),φ(t)在内的，满足双尺度递推关系的函数集合。其中，小波包系数的递推关系为：

(3)

式中，dj,n(k)为小波包经分解后第(j,n)节点所对应的第k个系数，节点(j,n)表示第j层分解的第n个频带。

由上述分析可知，小波包分解过程中对低频部分和高频部分进行了同步分解，对高频部分的分解提供了更为精细的信号分析方法[11]。

1.2 小波基选择

对同一信号来说，其小波包变换后在频域的稀疏度越高，其压缩率越高，且重构精度越高。而频域的稀疏度与小波包变换过程中所选取的小波基类型关系密切。目前，选择什么样的小波基能使信号在频域具有较高的稀疏度的方法研究还很少，还没有统一的选取标准。本文中采用实验的方法来选择适合对光纤振动信号进行稀疏分解的小波基。首先，从一套光纤周界报警系统中采样(采样频率20kHz)得到包括4种常见扰动(分别为正常信号、小扰动信号、大扰动信号、蓄意入侵信号，数据长度为2018×256个采样点)类型的光纤扰动信号作为测试样本。从测试样本中任意截取一段长度为256个采样点的振动信号，分别采用几种常用的小波基进行4尺度小波包分解，分别计算4尺度下的数学期望Ep(p=1,2,3,4)作为阈值Tp对小波包系数进行置零处理，并分别计算其稀疏度kp(即系数中为零系数占所有系数的百分比)，实验结果如表1所示。比较表1中数据，本文中选择sym7小波基对光纤振动信号进行小波包变换。

Table 1 Sparse degree of different wavelets

1.3 小波包分解层数选择

利用小波包对信号进行分解的层数与小波包系数的稀疏度密切相关。在实际应用中，应根据信号的特征选择合适的分解层数，以便获得最大信号稀疏度。本文中用实验的方法来分析小波包的分解层数与小波包系数稀疏度之间的关系。在第1.2节中的测试样本任意截取50段长度为256个采样点的光纤振动信号，分别采用sym7小波基对其进行2～6层小波包分解，分别计算各尺度下高频系数的数据期望作为阈值，对该尺度下的小波包系数进行置零处理，然后计算各尺度下小波包系数的平均稀疏度,如表2所示。

Table 2 Sparse degree of different decomposition layers/%

由表2中数据可以看出，随着分解层数的增加，小波包系数的稀疏度也增加；但到达一定层数时，稀疏度开始下降。所以，在实际应用中，必须对小波包变换的分解层数进行合理的选择，才能使信号在频域的稀疏度达到最大。

2 光纤振动信号自适应压缩感知

2.1 压缩感知原理

(4)

式中，s=〈x,ψi〉=ψiTx是该信号在ψ域的稀疏系数，T表示向量的转置，包含有k个非零项，且k≪N；x为在正交基矩阵ψ上的k稀疏表示。

构建一个和正交基矩阵ψ不相关的观测矩阵ΦM×N={φ1T,φ1T,…,φMT}，M为ΦM×N矩阵的行向量数，且M≪N，将信号x由高维空间投射到低维空间[12]：

y=Φx=ΦΨs

(5)

式中，y∈RM×1称为观测向量；ΦΨ称为传感矩阵，s的含义同(4)式。

根据压缩感知理论，信号的重构是一个欠采样条件下病态的求逆问题，即信号x是下式l0最小化问题的解，即：

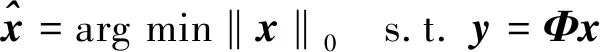
(6)

为了更容易求解，将 (6) 式的NP-hard问题转化为求解最小化l1的问题[13-14]。目前常用的方法有正交匹配追踪(orthogonal matching pursuit，OMP)算法[15]、基追踪(basis pursuit，BP)算法[16]等。

2.2 基于数学期望的阈值选取

为了充分体现小波包系数中大系数的分布情况，需重新定义数学期望的计算公式[17]。设数据序列x={xi}(i=1,2,…,n)，定义其数学期望为:

(7)

对光纤振动信号进行多尺度小波包分解后，利用 (7) 式计算小波包系数高频部分的数学期望作为阈值，对小波包系数进行置零处理。例如，任意截取第1.2节中所述测试样本中的一段长度为256个采样点的光纤振动信号进行2尺度小波包分解，2尺度下小波包系数各系数块的数学期望值为{613.54,19.44,3.72,4.36}，其中613.54为低频部分的数学期望值，高频各部分的数学期望中最大值为19.44，取该值作为2尺度下小波包系数的阈值T，对该尺度下的小波包系数进行置零处理，即：

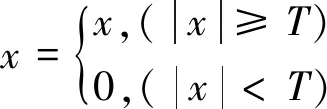
(8)

关于阈值选取对信号重构精度及压缩率的影响，在后面的实验分析中还将进一步讨论。

2.3 自适应小波包变换

光纤振动信号经小波包分解后，小波包系数的稀疏度可用数学期望表示，当小波包系数的数学期望越大时，说明大系数越多，其稀疏度越低[10,18]。根据第1.3节中的分析，采用小波包对光纤振动信号进行多层分解后，各尺度下的小波包系数的稀疏度是不同的，为了使信号在频域具有较高的稀疏度，采用相同的分解层数显然是不合理的。因此，本文中基于小波包系数的数学期望提出自适应小波包变换。方法如下:首先对光纤振动信号进行3层～5层小波包分解，然后计算各尺度下小波包系数高频部分的数学期望值，按照(5)式对各尺度下的小波包系数进行阈值处理。比较各尺度下的稀疏度，选择稀疏度最大的尺度作为信号的最终分解层数，从而完成自适应小波变换。

2.4 基于信息熵的信号分类

为了进一步提高信号的压缩率和重构精度，在对小波包系数进行阈值处理后，重新计算该尺度下各小波包系数块高频部分的数学期望E和信息熵H[19]，并根据E和H对小波包系数块进行分类。

(1)低频系数块。是指小波包系数块中的低频部分，包含着信号的最主要信息，包含了大量的大系数，属于不稀疏信号，如果仍采用压缩感知方法进行处理，不但会增加较大的计算量，也会造成信号重构精度的降低。所以这部分系数块采用线性直接传输方式，一方面保证了信号的重构精度，另一方面也降低了算法的运算时间。

(2)无价值系数块。当系数块的数学期望E=0时，说明该系数块全为0，这类系数块在信号的数据压缩、传输和重构过程中都没有利用价值，所以没有考虑的必要，称为无价值系数块，这类系数块不参与数据的传输与存储。

(3)特殊系数块。如果系数块的信息熵为零或数学期望小于某一特定值C时，归类为特殊系数块。

根据信息熵的定义，当系数块的信息熵为零时，说明该系数块要么全为0，要么只有一个不为零的大系数；又因为其数学期望不为0，则易知该系数块中只有一个不为零的大系数。

当系数块的数学期望小于某一特定值C时，C值大小应根据实际需要进行确定。对有N个系数的系数块，设阈值为T，其中包含有k个大系数；为了确定C值，假定该系数块中的k个大系数均为阈值T，此时该系数块的数学期望为kT/N，那么该系数块的C=kT/N；显然，当某系数块的数学期望小于C值时，则其大系数的个数必然小于k。

由以上分析可知，特殊系数块就是指只包含有少数几个大系数的小波包系数块。在传输时，特殊系数块只需要传输大系数值及其相应的位置，即采用编码方式进行网络传输。

(4)压缩感知系数块。除无价值系数块和特殊系数块外的其系数块都归类为压缩感知系数块。这类系数块的数学期望和信息熵均不为零，说明其中包含的大系数较多，采用压缩感知方法进行处理比较合适。

2.5 信号重构

信号的重构工作包括小波包系数重构和小波包重构。小波包系数重构根据系数块的类型选择相应的重构方法：(1)低频系数块直接恢复，并摆放在小波包系数的低频部分；(2)特殊系数块按系数值及位置编码恢复小波包系数及其所在位置，其余位置用0填充；(3)压缩感知系数块采用压缩感知重构方法(例如OMP)恢复数据，并摆放在小波包系数块的对应位置；(4)小波包系数块的剩余位置用0填充。

完成小波包系数恢复(重构)后，再对小波包系数进行小波包逆变换，完成信号重构。

根据上述分析，得到基于小波包实现周界报警信号的自适应压缩感知与信号重构[14,20]的基本流程如图2所示。

3 实验与分析

3.1 信号压缩感知与重构评价指标

为了比较光纤振动信号的压缩感知和重构性能，引入信号压缩比(compression ratio，CR)RCR评价信号的压缩效果：

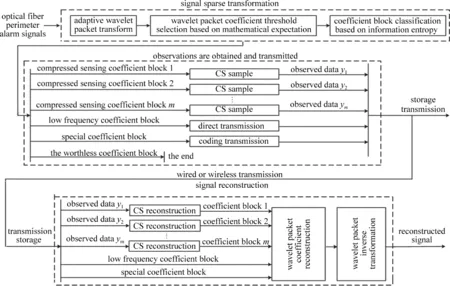
Fig.2 Flow chart of adaptive compresssion sensing and signal reconstruction

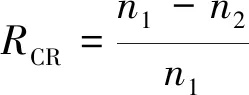
(9)

式中，n1,n2分别为信号压缩前、后的数据量。引入PSNR(RPSNR)作为信号重构精度的评价指标：

(10)

通过实验得到，对周界报警信号来说，采用PSNR作为信号重构评价指标时，当重构后信号的RPSNR>40dB时，信号的特征信息能够得到完整的保留。

3.2 基于数学期望为小波包阈值的合理性验证

从第1.2节中所述的测试样本中任意截取5段长度为256个采样点的光纤振动信号，分别对其进行4层小波分解，计算4尺度下小波系数高频部分的数学期望E，分别选用1.2E，E，0.8E作为阈值T，对小波包系数高频部分进行置零处理。然后采用本文中的小波系数分类和信号重构方法得到重构后的光纤振动信号。分别计算3种阈值T下的信号压缩率/重构精度,结果如表3所示。

由表3中数据可以看出，阈值较小时，小波包系数稀疏度较低，压缩率也低；阈值较大时，小波包系数稀疏度提高，压缩率提高。特别是，当阈值为1.2E时，信号的重构精度较其它两种方法低，这是因为阈值过大，基于该阈值处理小波包系数会使稀疏过度，丢失原始信号中一些有用的特征信息，造成信号重构精度下降；而当阈值为0.8E时，信号重构精度较阈值为E时稍低，这是因为前者虽然保留了更多信号的特征信息，但由于稀疏度下降，所以重构精度也有所下降。综上所述，选择小波包系数的数学期望E为阈值时，其压缩率和精度都比较高，所以该阈值大小选取最为合理。

Table 3 Effect of threshold size on signal compression/reconstruction accuracy

different signalsegmentthe zero threshold of wavelet packet coefficient1.2EE0.8Esignal segment 1/(%/dB)73.8/40.468.5/44.765.2/44.6signal segment 2/(%/dB)73.4/41.270.1/43.966.1/43.7signal segment 3/(%/dB)67.5/42.763.8/45.259.9/44.3signal segment 4/(%/dB)72.2/40.569.2/42.063.6/42.2signal segment 5/(%/dB)71.6/39.267.3/43.362.4/41.9

3.3 本文中算法的合理性验证

仍采用第1.2节中的测试样本信号，任意截取256个采样点，分别采用小波变换和小波包变换进行固定4尺度分解，并分别选取4尺度下小波系数、小波包系数据的数学期望作为阈值对小波系数、小波包系数进行置零处理。再将该段信号采用本文中所述算法进行处理。在保证3种算法具有相同压缩率的前提下，对信号进行重构的结果如图3所示。

Fig.3 Signal reconstruction effect of different algorithms

a—original signal b—the algorithm in this paper c—wavelet transform d—wavelet packet transform

从图3可以看出，3种算法在相同压缩率前提下，小波变换方法的信号重构效果最差；而小波包算法和本文算法的重构效果相差不大，但将波形放大后进行比较，还是可以看出本文中所述算法的重构效果优于小波包算法。

3.4 自适应压缩感知算法的压缩率验证

从第1.2节中的测试样本中分别截取光纤传感器常见的4种输出信号类型：正常信号、小扰动信号、大扰动信号和入侵信号各50段，每段信号长度均为256个采样点。分别采用本文中算法对信号处理，并计算4种信号的平均压缩率,如表4所示。

Table 4 Compressibility of fiber vibration signal

从表4中的数据可以看出，4种光纤振动信号的压缩率基本一致，可见本文中算法是适合对光纤周界报警系统的各种输出信号进行处理的。

3.5 各种算法综合性能比较

从第1.2节中的测试样本中任意截取1500段长度为256个采样点的光纤振动信号，首先采用sym7小波基分别对1500段信号进行4尺度小波、4尺度小波包稀疏变换，并计算4尺度下的小波系数、小波包系数的数学期望作为阈值，并对小波系数、小波包系数进行置零处理，并采用OMP方法完成信号重构；然后采用sym7小波基利用本文中算法对1500段信号进行处理。分别计算3种算法的平均压缩率、信号的平均重构精度以及各算法处理1500段信号总消耗时间，计算结果如表5所示。

Table 5 Comprehensive performance of various algorithms

比较表5中的数据明显可以看出，小波包算法的压缩率和重构精度优于小波算法，这是因为小波包算法对信号的高、低频部分进行同频分解，信号的稀疏度提高，且保留了更多信号的特征信息。但小波包算法由于增加了信号的处理过程，因而在计算耗时上比小波算法略有增加；本文中算法采用数学期望作为阈值对小波包系数进行置零处理，并自适应地选取了最佳分解尺度，进一步提高了信号的稀疏度，因而算法的压缩率和重构精度比小波包算法更好。同时，本文中算法利用数学期望及信息熵对小波包系数进行分类处理，优化了信号处理方法，提高了信号处理速度，因而运算速度得到提高。

由于时域下的光纤报警信号表现复杂，各分块信号的信息特征差异较大，采用固定的稀疏字典对各分块信号进行稀疏表示仍不可能使信号的稀疏度达到最优。因而可以考虑根据信号的具体特征构建过完备字典，使信号在变换域的稀疏度进一步提高，从而可以进一步提高信号的压缩率和重构精度。这是下一步工作的研究重点。

4 结 论

本文中采用小波包自适应压缩感知方法处理光纤周界报警信号，主要解决了3个方面的问题：(1)采用小包波对光纤周界报警信号进行稀疏变换，对仍含有丰富信息特征的高频部分进行分解，较好地保留了信号的信息特征，并进一步提高了信号在频域的稀疏度，较大程度地提高了信号的压缩率和重构精度;(2)基于小波包系数高频部分的数学期望实现自适应小波包稀疏变换，使信号在频域的稀疏度得到进一步提高,在保证一定重构精度的前提下，具有较高的信号压缩率;(3)基于小波包系数块的数据期望和信息熵对小波包系数块进行分类处理，减少了观测数据，较大程度地降低了网络传输带宽和算法的运算速度，便于对大规模数据进行处理，提高了压缩感知方法在光纤周界报警系统中的应用价值。

总之，采用本文中所述方法对光纤周界报警信号进行压缩感知与重构时，与传统算法相比，具有更高的信号压缩率和重构精度，且具有较低的网络传输带宽和较高的运算速度。