基于灰狼算法优化PID的机器人路径跟踪控制

文/朱敬旭辉 赵景波 薛秉鑫

自从机器人路径跟踪问题引起各界学者的注意，直到上个世纪九十年的之后，才开始了广泛的研究。历经20多年的发展，众多研究人员研发出了多种路径跟踪的控制方法。其中包括：PID控制、反步法、智能控制方法等多种控制方法。

本文采用融合动力学进行分析，首先建立了两轮差速驱动移动机器人的运动学及动力学模型，并采用反步法设计了移动机器人路径跟踪控制规律，以此来计算控制量的期望值；然后提出了基于灰狼算法优化的PID控制，采用灰狼优化算法对PID控制参数进行自整定以提高控制系统的动态性能；最后仿真表明，利用本文提出的控制算法能够有效稳定地控制移动机器人完成路径跟踪任务。

1 移动机器人路径跟踪控制模型

移动机器人的经典模型是两轮差速驱动模型，其位置姿态图如图1所示。

根据图1，建立两轮差速驱动机器人的运动方程，如式（1）所示：

其中，(x,y)是机器人实际环境中的坐标位置，v是机器人在纵向方向上的速度，ω是机器人平面转动的角速度，θ是机器人行进方向与坐标X轴的夹角，即方向角。根据机器人的位置(x,y,θ)与姿态(v,ω)解得机器人的位置姿态误差微分形式为：

进一步得到：

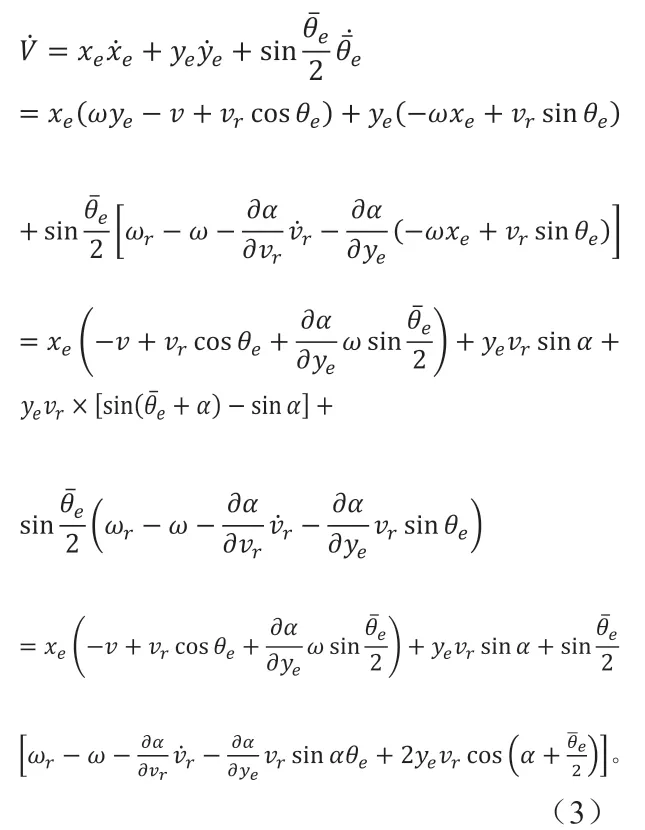
计算可得控制规律：

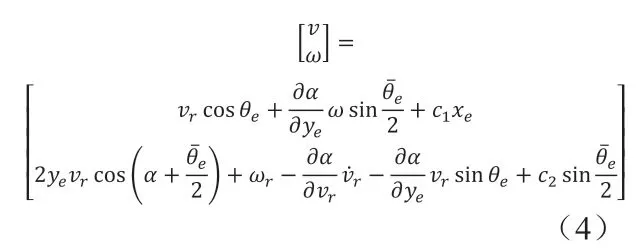
其中c1，c2均为常数。

将式（4）代入式（3）得：

由Lyapunov稳定性理论可知此系统具有稳定性。

2 移动机器人路径跟踪控制器设计

在给定移动机器人的跟踪路径后，确定期望控制输入v和ω，根据实时反馈的位姿(x,y,θ)，比较期望位姿和实际位姿得出地理坐标偏差，再变换到移动机器人坐标系（纵向x轴，以机器人中心左向垂直为y轴）。通过控制器控制输入v和ω，逐步调整到期望位姿。机器人坐标系的偏差：

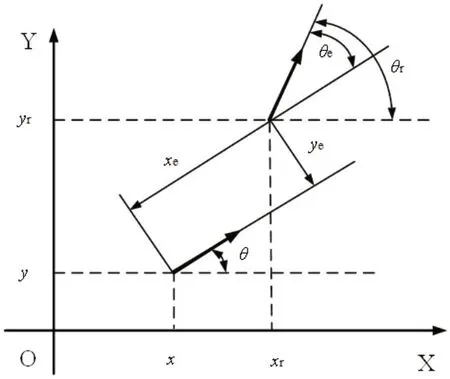
图1：移动机器人位姿图

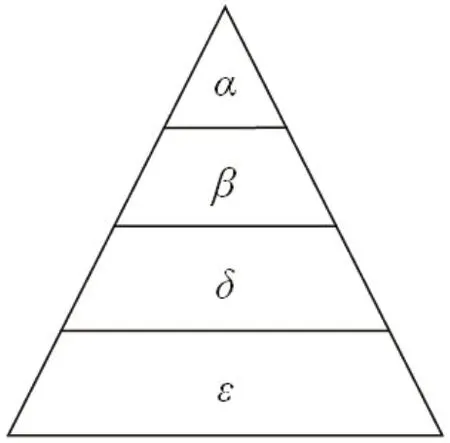
图2：狼群等级结构图

式中，(xd, yd, θd)为期望位姿，(xr, yr, θr)为机器人位姿，(xd-xr, yd-yr, θd-θr)为实际坐标位姿偏差。路径跟踪的最终目标是求解合适的(v,ω)满足：

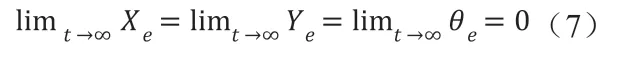
3 灰狼算法原理

灰狼群体中有着严格的层级制度，如图2所示，其层级由高到低分为α、β、δ、ε四类，所属层级越低的，其数量越多。低级狼受控于高级狼的命令，但高级狼也会受到低级狼的挑战，如果低级狼挑战成功将会取代高级狼的地位。当狼群中高等级的狼缺失时，会由β狼接替α狼的位置。狼群在追捕猎物时，由等级最高的狼带领狼群对猎物进行有组织的围攻，α、β、δ狼引领着ε狼逐渐向猎物靠近，逐步缩减对猎物的包围范围，然后伺机以极快的速度对猎物发起进攻。

表1：常规PID控制曲线路径跟踪实验数据

表2：基于灰狼算法优化的PID控制曲线路径跟踪实验数据

GWO对狼群组织和狩猎方式的模拟，如图3所示。将狼群分成α、β、δ、ε四组，由α、β、δ带领ε向着目标搜索，在优化过程中，不断更新α、β、δ、ε的位置，见式（8）至式（12）。

其中，t为当前迭代次数，Pk表示猎物的位置，P表示灰狼的位置向量，C为随机因子，r1、r2为[0,1]随机数，max为最大迭代次数，a为收敛因子。D表示狼与猎物的距离。A控制搜索范围，当|A|>1时，表示搜索范围扩大，为全局搜索；当|A|<1时，表示搜索范围收缩，为局部搜索。

因为α、β、δ距离目标的距离最近（即适应度最高），所以可以利用α、β、δ所在位置信息引导ε判断出目标的大体方位，对猎物进行逼近，见式（13）和式（14）：

其中，Pα代表α当前方位，Pβ代表β当前方位，Pδ代表δ当前方位。式（15）计算出ε的第t+1次迭代位置：

4 GWO优化PID算法设计

4.1 基本思想

图3：狼群位置更新原理

图4：GWO优化PID的系统结构图

将PID控制器的三个参数(KP, KI, KD)作为灰狼的位置向量，在给定的搜索空间内，灰狼在适应度值最优的前三只狼α、β、δ的带领下调整自己的位置，从而逐步逼近最优目标。GWO优化PID的系统结构如图4所示。GWO根据系统的运行状态，不断地调整PID的三个参数，从而使控制系统的性能指标和控制效果达到最优。

4.2 适应度函数的确定

PID控制器的优化设计就是选择合适的KP、KI和KD，使得系统各项性能指标和控制效果达到最优。在控制系统中，常用的误差性能指标有ISE、ISTE和ITAE，本文选用误差绝对值时间积分函数ITAE指标作为目标函数，其定义为：

其中，t为时间，e(t)为系统给定值与系统输出的偏差。

图5：常规PID控制曲线跟踪路径及误差图

图6：基于灰狼算法优化的PID控制曲线跟踪路径及误差图

4.3 GWO优化PID算法流程

采用GWO算法优化PID参数的基本流程如下：

Step 1：给出PID三个参数的取值范围，并在此范围内随机初始化狼群；

Step 2：按照式（19）计算每只狼相应的适应度值；

Step 3：对每只狼按适应度值排序，将适应度值最优的前三只狼分别设置为α、β、δ。

Step 4：根据式（8）-（11）、式（13）-（14）和式（16）-（18）更新所有ε狼的位置；

Step 5：更新参数a、A、C；

Step 6：判断是否达到最大迭代次数max或其他结束条件（α的适应度值大于或小于某一适应度限值），若满足则继续执行，否则，跳转至Step 2；

Step 7：输出最终α的位置，即得到最优的PID参数。

5 路径跟踪仿真研究

为验证本文提出的基于灰狼算法优化的PID控制在移动机器人路径跟踪控制中的有效性和可行性，基于第一节中建立的两轮差速驱动移动机器人运动学模型和控制模型，将本文所提控制算法用于移动机器人路径跟踪控制仿真实验，并将该算法与常规PID控制进行了对比实验。考虑到在实际情况中路径基本可以分解为直线路径和曲线路径，因此本文主要针对曲线路径进行路径跟踪控制仿真研究。

在曲线路径跟踪仿真中，选择常规PID控制参数为：KP=45，KI=0，KD=5，常规PID控制和基于灰狼算法优化的PID控制曲线路径跟踪控制结果分别如图5和图6所示，两种控制算法的相应实验数据分别如表1和表2所示。

以上仿真结果表明，本文所提控制算法在曲线路径跟踪控制中同样取得了较为理想的控制效果，同时说明了该控制算法具有较好的鲁棒性，在解决路径跟踪控制问题时具有一定的优势，可用于移动机器人路径跟踪任务。

6 总结

本文提出并使用的灰狼算法优化的PID控制完成了对两轮差速驱动移动机器人路径跟踪控制问题的研究。首先建立了移动机器人路径跟踪控制模型并证明了其稳定性；然后详细介绍了灰狼算法优化的PID控制，并设计了移动机器人路径跟踪控制器；最后通过仿真对比实验验证了本文所提控制算法在移动机器人路径跟踪控制中的有效性和可行性。最后仿真结果表明利用本章提出的控制算法可以实现移动机器人对期望路径的有效可靠跟踪。