扭转梁系统可靠度与载荷谱的相关性研究

韦仲宁，万茂林

(广州小鹏汽车科技有限公司汽车技术中心，广东广州 510640)

0 引言

扭转梁式后桥具有构造零件数量少、制造工艺较简单且成本较低等优势，在经济型乘用车、新能源车中应用广泛。扭转梁式后桥由一根V形或U形钢板横梁作为主体，焊接有纵臂、轮毂支架等，结构如图1所示。供应商会根据产品设计要求说明书(Specification of Requirements,SOR)设计、制造扭转梁，在不了解可靠度、置信度要求且未有载荷谱的条件下，在设计验证阶段进行样本量不小于5件的零部件试验，在产品验证阶段进行样本量不小于5件的零部件试验，且系统寿命要满足整车设计里程的可靠性要求。

图1 扭转梁结构示意

新车型开发过程中，扭转梁SOR与DVP(Design Verification Plan)试验规范，主要是根据以往的平台项目经验或其他厂家数据编制制定，无该款车型整车试验场的相关数据，导致整车道路试验与室内系统台架试验结论不同、试验场故障与台架试验故障不一致。因此，采集试验场的道路载荷谱、六分力等相关数据，研究扭转梁载荷谱与可靠度相关性，保证系统台架试验与整车道路试验匹配，做到校正零部件、系统试验台架规范，对扭转梁的开发与验证具有重要的意义。

本文作者根据整车可靠性目标，基于各系统零件数量、安全件数量分解可靠性目标至系统总成上；再通过采集车轮六分力与扭转梁应变敏感部位来进行伪损伤分析,获取扭转梁损伤较大的主要工况,累计所有主要工况的损伤值。再根据威布尔理论进行分析，编制出达到系统可靠度目标的扭转梁DVP台架试验规范。

1 可靠性理论

1.1 系统可靠度

汽车是由成千上万个零件组成的交通运输工具，也是一种结构较为复杂的机电产品。由零件按照其作用分别装配在一起，各自具有一定的功能，相互间有一定的配合关系。将所有的装配单位有机地组合起来，就组成了完整的汽车。

一个系统是由一组零件(元件)、部件、子系统或装配件(统称为单元)构成的，完成期望的功能，并具有可接受的性能和可靠性水平的一种特定设计。

1.2 整车可靠性分解方法

汽车各系统中，选择关键单元，先分解系统，再组合计算。

各串联子系统的如图2所示，可靠性最差的单元对系统的可靠性影响最大，且系统内组件增加，可靠性水平降低可靠度计算方法：R1=RA1·RB1·RC1。

各并联子系统如图3所示，并联条件下，随着组件数增加，系统可靠度对组件的可靠度依赖越来越小，可靠度计算方法：R2=1-(1-RA2)·(1-RB2)·(1-RC2)。

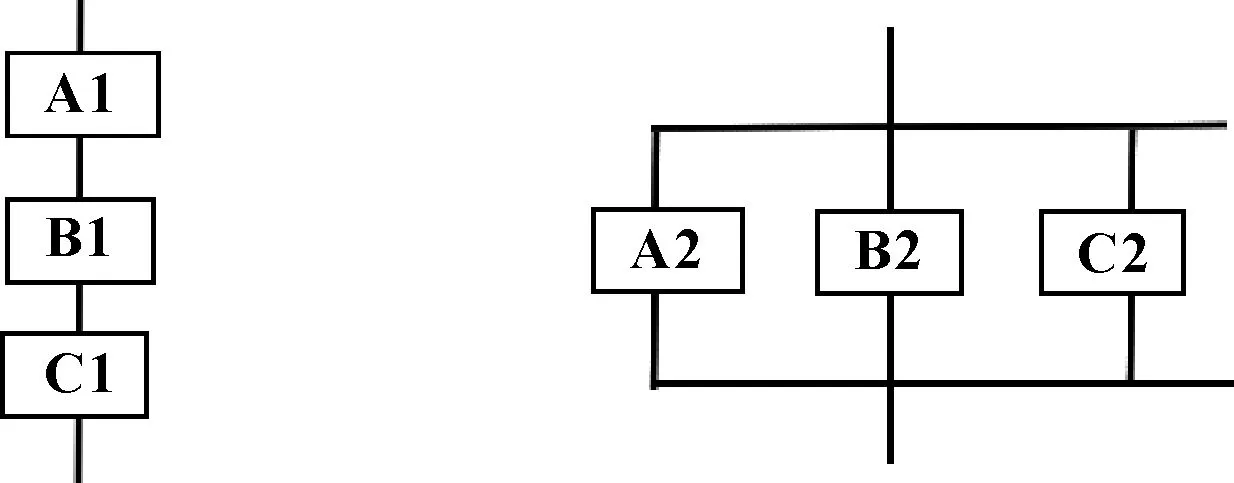
图2 串联系统 图3 并联系统

基于以上串联系统与并联系统计算方法，分解某车型的在8年或16×104km的可靠性如表1所示，其中整车统一设置置信度为C50，扭转梁系统可靠度为R97C50。

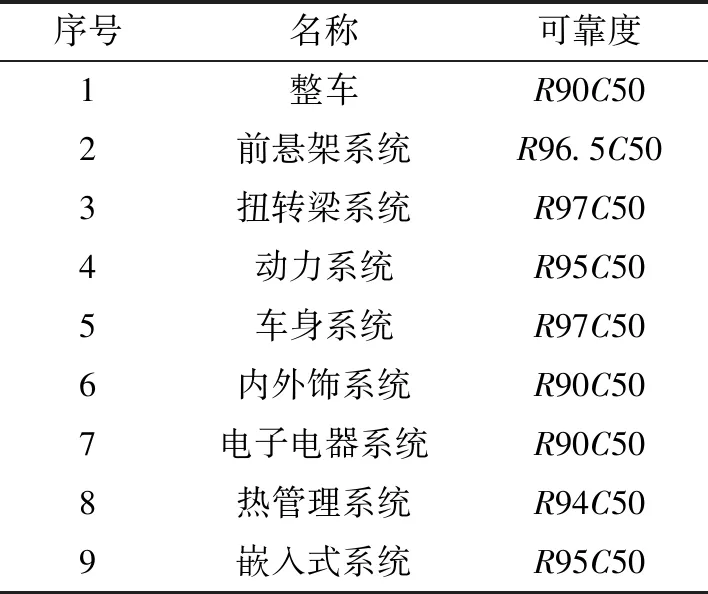
表1 整车系统可靠性分解

2 载荷数据采集及处理

2.1 应变片传感器

箔式电阻应变片是一种基于应变-电阻效应制成的，用金属箔作为敏感栅的，能把被测试件的应变量转换成电阻变化量的敏感元件，可参考图4。

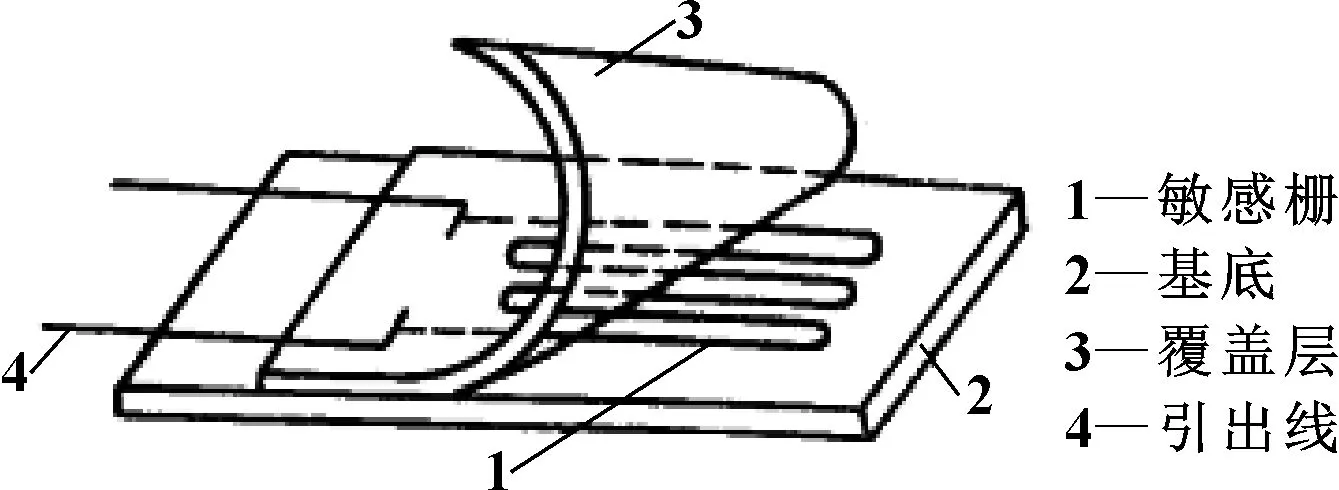
图4 电阻应变片

电阻应变片是用来测量物体受力变形产生的应变的一种传感器，可以用来测试不同零部件的应变、力、扭矩等信号，其基本原理可简述为：将应变片固定粘贴在测试件上，使其随测试件一起受到载荷作用，其中的金属箔材会随着测试件的形变而伸长或缩短。应变片所选用的金属材料，如金属箔材，在一定范围内，机械伸长或缩短时其电阻也会随之成正比变化：

ΔR/R=Kε

(1)

式中：R为应变片原电阻值；ΔR为伸长或压缩引起的电阻变化；K为应变片灵敏度系数，一般为2.08±1%；ε为应变。

通过测量电阻的变化，就可以对应变进行测定，进而可转化为测定力、力矩等。箔式电阻应变片具有体积小、动态响应快、测量精度高、使用简便等优点。

2.2 应变片选择

箔式电阻应变片按照应变片的形状可以分为单片、应变花、剪切应变片，T形应变片等，具体如图5所示。

图5 不同类型的应变片

根据需要的应变信号和试件结构来选择应变片型号，具体可参照表2。

表2 应变片的选择

2.3 确定测量点位置

测点的选择和布置对能否正确了解结构的受力情况和实际正确的测量有很大的影响。一般应以最小的测点达到足够反映结构受力状态为原则。为此，一般应考虑：

(1)预先对结构进行大致的受力分析，预测其变形形式和危险面，根据受力分析和测试要求，结合有限元分析和实践经验最终确定测点。

(2)在截面尺寸急剧变化的部位或因孔、槽导致应力集中的部位，应适当多布置一些测点，以便了解这些区域的应力梯度情况。

(3)根据扭转梁有限元CAE分析结果、扭转梁系统台架试验的要求，确定采集的应力位置。

扭转梁关键位置应变信号，具体见图6和表3。

图6 扭转梁系统测量载荷位置

表3 采集通道名称和位置描述

2.4 数据采集

此次测试采用LMS数据采集系统在试验场进行信号采集，共30个信号通道。按照满载的条件对前悬轴荷、后悬轴荷分配进行均匀配重，标准胎压，然后在车辆静态情况下对采集信号进行归零处理，试跑2圈后，检查信号无误，开始试验。

此次试验具体工况如下：外环1、外环2；内环1、内环2；方坑1 & 2、方坑3；搓板路制动、中制动、全制动；陡坡路(山路)、城市路工况；13°倒坡、16°倒坡；High-G、L-转向、直角转向。

2.5 检查数据

查看数据是否存在奇异点、漂移等，主要是异常峰值点、趋势项等，如确实存在，可通过滤波、平衡偏斜法等方法来消除奇异点和趋势项。一般通过Crest因子大小来检查是否已经去除奇异点，Crest因子αCrest为

(2)

当Crest因子在1～8之间时，可认为该数据质量好，已消除奇异点。

2.6 某车型扭转梁载荷数据分析

2.6.1 滤波

一般滤波过程采用巴特沃思滤波器进行低通滤波，路面的激励信号频率一般在50 Hz以下，将高于50 Hz以上的信号滤掉即可，具体可通过频域分析处理(PSD，自功率谱密度)来观察信号的频率结构，从图7可以看出信号频率成分主要集中在30 Hz以下。

图7 各通道信号自功率谱密度曲线

2.6.2 信号时域的处理

在山丘路况采集数据，进行时域一致性处理，结果如图8所示。

图8 山丘信号

3 累积损伤分析

3.1 车轮六分力损伤分析

通过LMS Tec-Ware模块分析车轮轮心力在各工况的“累积损伤”，从而判断各个工况对Fx、Fy、Fz的影响，具体如图9和表4所示。

从图9中可以看出：轮心力Fx在搓板路甲、方坑工况中受影响比较明显，轮心力Fy在转向角度较大的直角转向、High-G、L-转向中受影响比较明显，轮心力Fz在内环1、方坑、石块路甲、搓板路甲、石块路丙、石块路乙中比较明显。

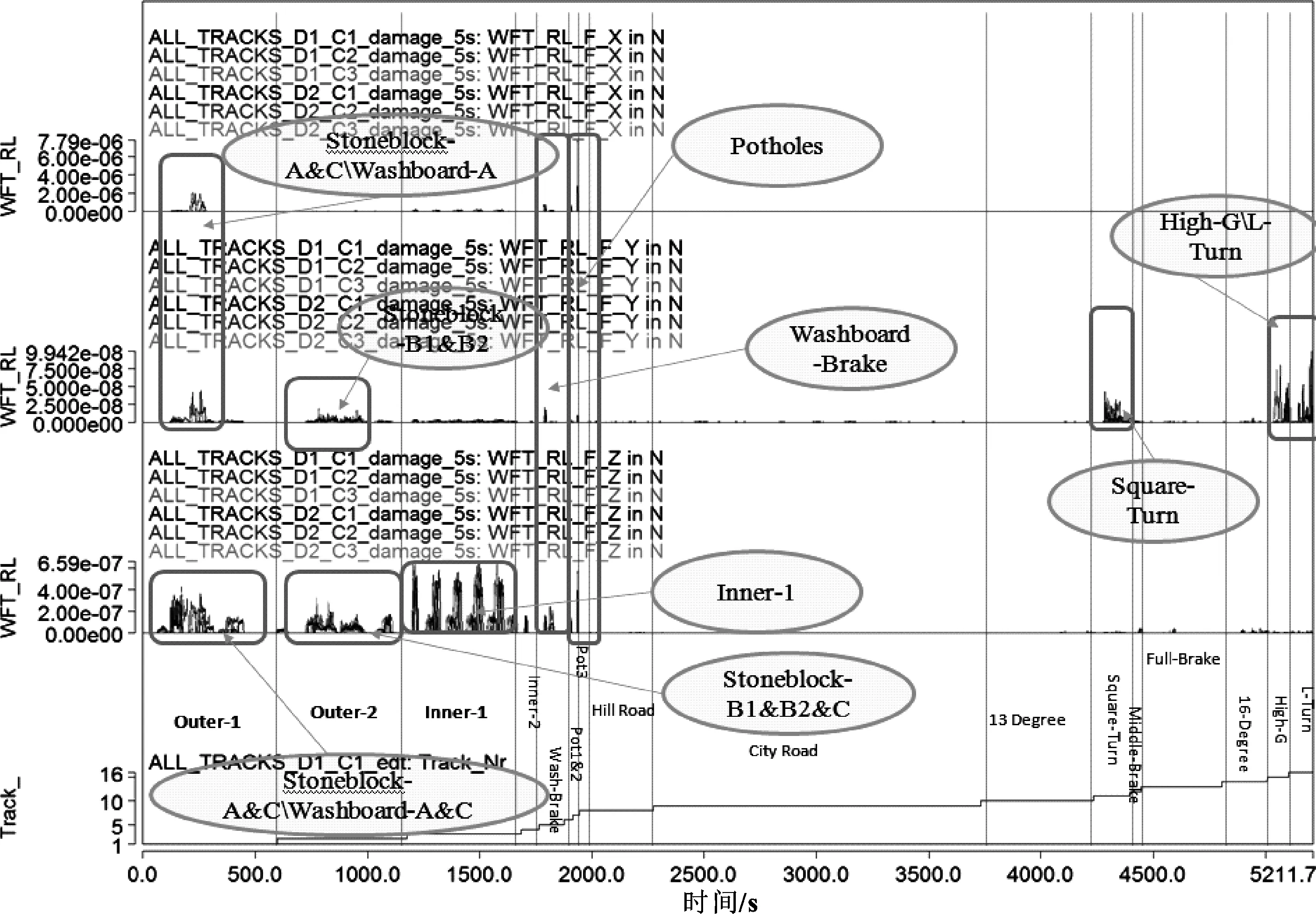
图9 轮心力在各工况的“累积损伤”

表4 各工况对Fx、Fy、Fz的影响

3.2 后扭转梁应变损伤分析

后扭转梁的激励响应主要由地面传递到车轮，车轮再传递到后扭转梁，因此车轮与后扭转梁的激励响应是一致的，这点可从“累积损伤”的趋势波动看出来，波动程度越大，代表损伤程度越高，具体案例分析如图10所示。可以看出：RL-2很明显直接受Fx的影响，RL-3&4主要在扭曲路乙受Fz的影响。

通过分析后扭转梁上的应变在各工况的“累积损伤”，比较分析在试验过程中各个工况对应变的影响。以应变花8、9、10在各工况的“累积损伤”为例，具体如图11所示。

从图11中可以看出各工况对应变的影响，结合前面所述的各工况对车轮轮心力的影响，并考虑到“累积损伤”影响的大小，有些工况对轮心力影响有限，可以忽略。因此可以得出车轮轮心力与后扭转梁测点应变的主要损伤体现，具体如表5所示。

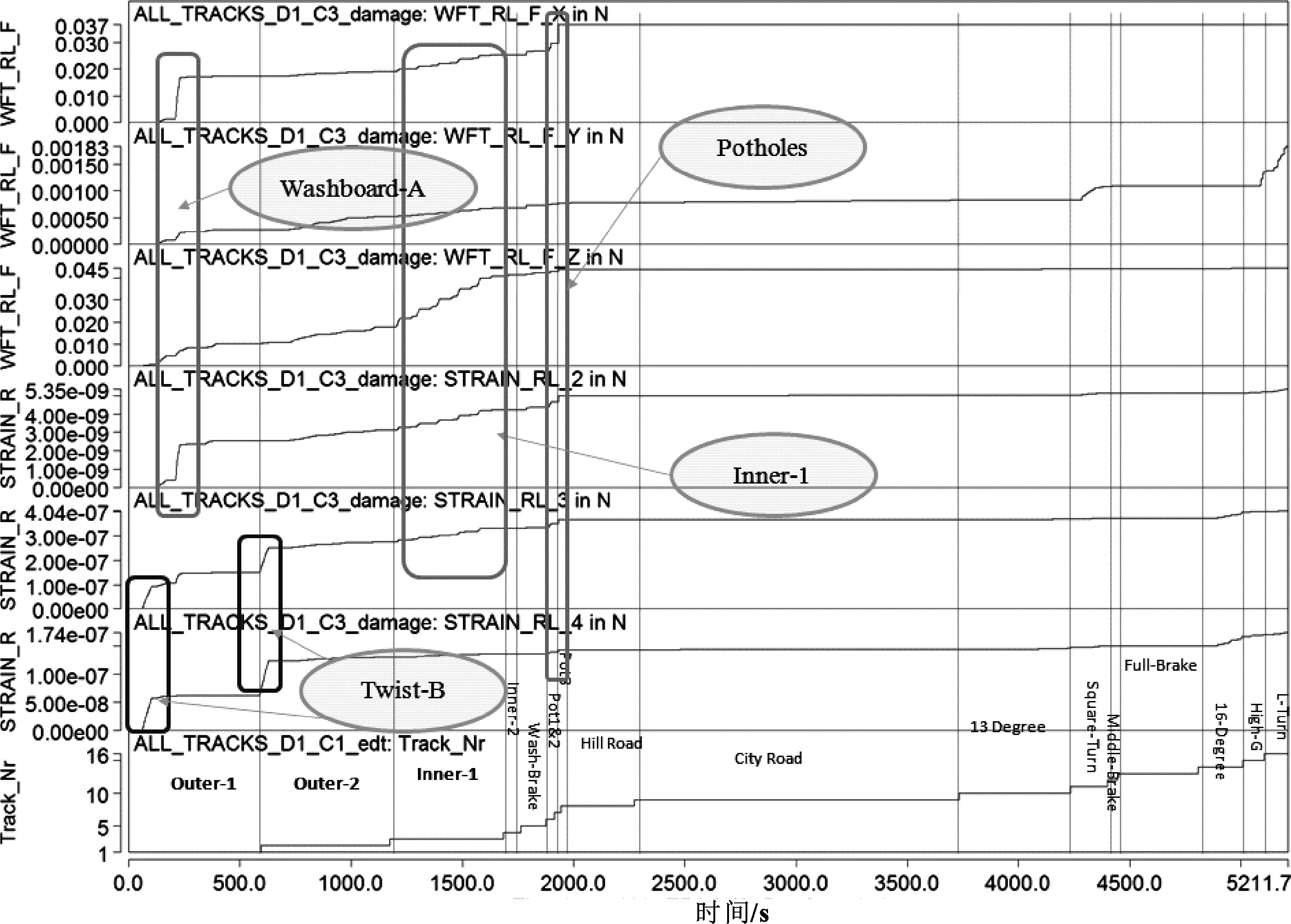
图10 轮心力与应变“累积损伤”波动趋势

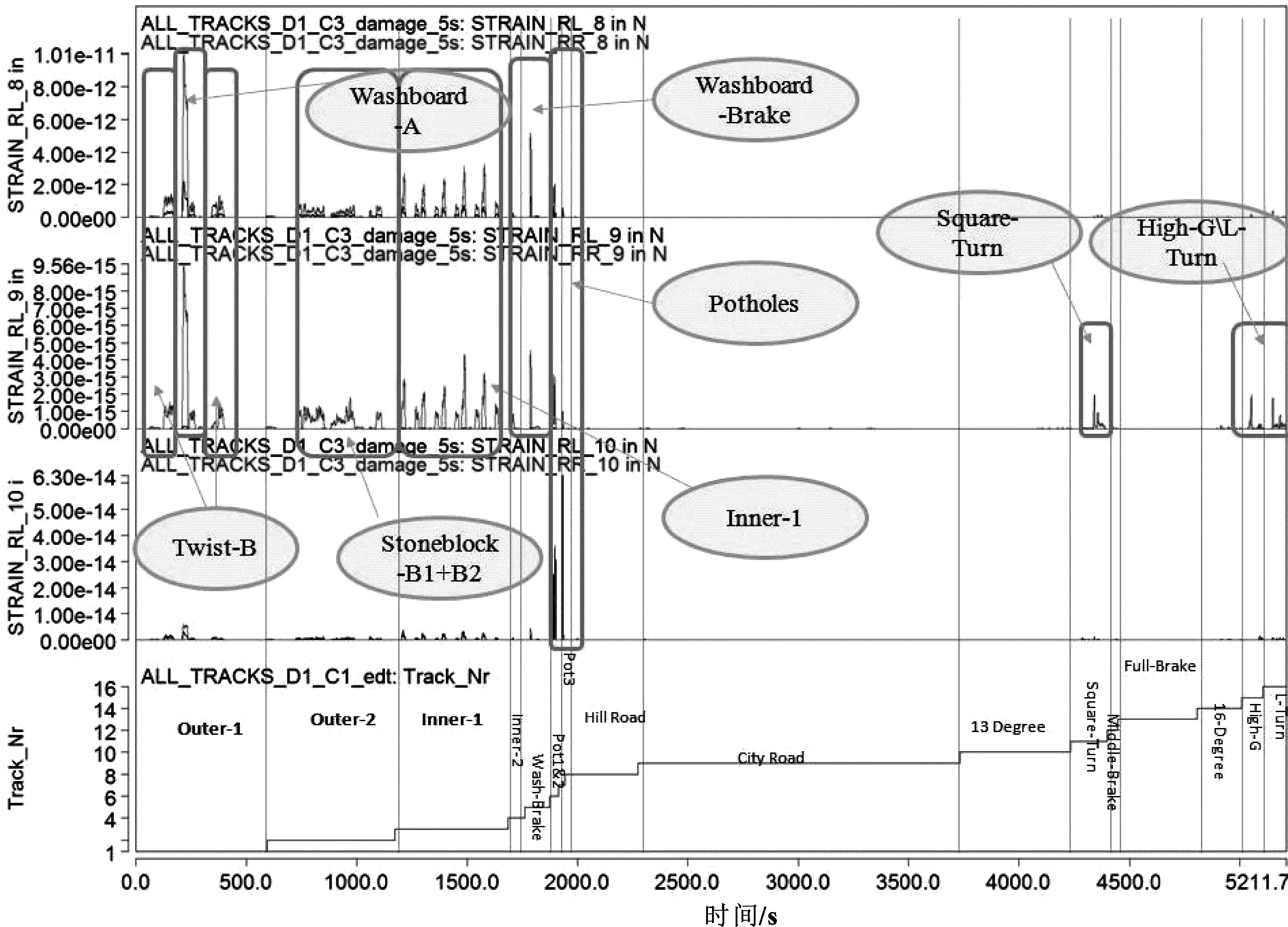
图11 应变花8/9/10在某工况下的“累积损伤”

表5 各工况对应变的影响

3.3 损伤累积计算

基于某车企耐久规范，循环总数6 922次等效8年或16×104km里程进行分析。

根据表6中得出，等效8年或16×104km的损伤累计0.268，损伤累计达到1.0时失效。安全系数K=1.2，即损伤值为：0.268×K=0.321 6，即求出在试验台架可以完成1/0.321 6≈3.1倍寿命加载扭转梁不失效、不开裂。

表6 常规耐久试验损伤分析

3.4 试验样品与试验可靠度

试验的可靠度由试验样品数及采用的置信度水平决定，其关系由

R=(1-C)1/N

(3)

或者可以变化为

(4)

式中：R为要求达到的试验可靠度；C为置信水平；N为试验样本数。

基于扭转梁试验台架可以达成3.1倍寿命加载不失效、不开裂，利用Minitab 软件计算扭转梁系统为达到R97C50的指标要求需要的试验样本数量关系，如表7所示。

(1)基于累计损伤，对比台架试验损伤，计算出扭转梁系统在试验台架上等效道路试验8年或16×104km的最大循环次数为46 300次，即单个样本量在试验台架上最大可加载143 968次循环。由表7可知，在R97C50指标要求下，2个样本量至少要3.37倍寿命加载才能达到指标要求，超过扭转梁系统样本所能承受的3.1倍寿命加载。

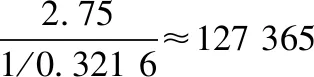
由表7可知：3个扭转梁试验样本，最大可靠度为R97.6C50；4个样本最高可靠度为R98.2C50。

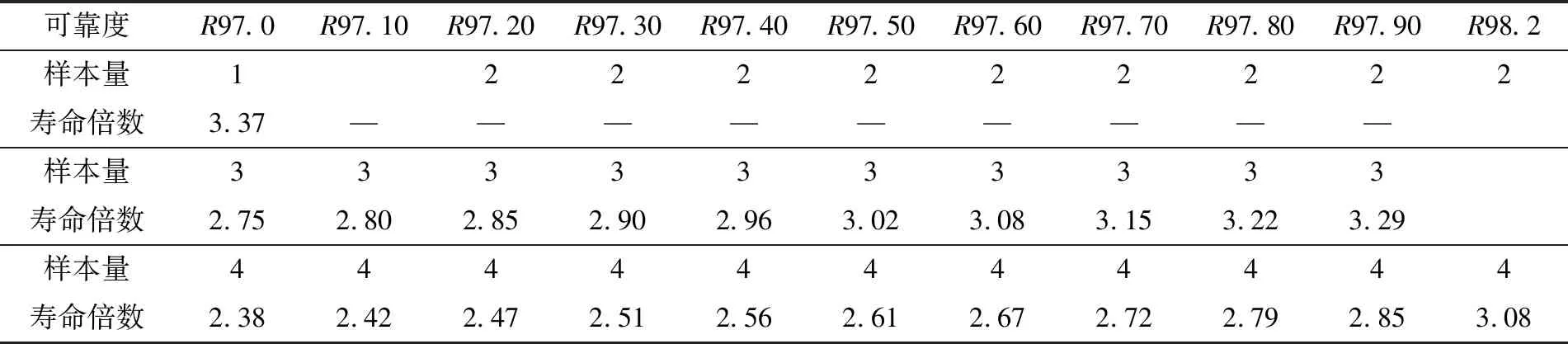
表7 威布尔回归模型需要的样本量估算

4 台架验证

扭转梁系统试验台架如图12所示。在扭转梁关键部位喷上白漆, 以便观察裂纹。输入127 365次循环驱动谱, 每隔3万次加载循环后，停止台架试验进行检查。当加载至145 000次循环后扭转梁结构出现开裂。通过室内道路模拟耐久试验结果与路试结果的对比表明, 两种试验出现的故障类似，如图13所示。

综合试验台架与道路试验进行分析，在整车分解要求达到R97C50要求，台架试验仅需要3个样本，每个样本加载127 365次循环载荷；整车需要23部样车进行耐久试验，所有试验车辆均无扭转梁系统问题，才可满足R97C50要求。

图12 扭转梁系统试验台架

图13 扭转梁系统开裂失效位置对比

5 结论

根据整车可靠度目标，分解到扭转梁系统上的要求是R97C50，通过试验场道路载荷谱采集与“累计损伤”的理论分析，计算出台架需要加载循环次数。同时运用威布尔理论计算分析获取最优样本量及加载循环数，从而以最优样本量、加载循环次数达成整车系统可靠度分解要求，节约整车试验成本与开发周期。