基于阻尼耗能支撑模型的建筑钢结构抗震稳定性检测方法

陈 颖

(福州外语外贸学院 理工学院，福建 福州 350202)

0 引言

本文提出基于阻尼耗能支撑模型的建筑钢结构抗震稳定性检测方法，首先建立建筑钢结构的支撑有限元模拟分析模型，然后采用阻尼耗能支撑结构特征分析方法进行建筑钢结构抗震稳定性的量化评价，实现建筑钢结构抗震稳定性检测。

1 建筑钢结构的支撑有限元模拟

1.1 地震波的转移状态

首先建立建筑钢结构抗震稳定性自动检测的主要物理参量联合分布模型，模型中不仅需要考虑地震动时长T，单位为s，还需考虑在地面震动情况下，钢结构稳定系数φ 的变化情况:

利用物理参量联合分布模型建筑钢结构抗震稳定性检测的模型特征匹配，使用一个非线性微分方程yi(t)对建筑钢结构抗震稳定性的特征进行检测，则建筑钢结构的抗震预应力分配，满足:

式中，ti表示相应周期。其中，在自复位阻尼耗能支撑约束条件下，得到建筑结构抗震稳定特征表达式为:

式中，zi是阻尼耗能支撑分布形态特征量，β 为载荷分离特征量。采用地震波输出振动特征测试方法［4］，得到地震波的转移状态方程为:

经上述得到地震波的转移状态，通过式(4)的计算，可得到地震波的传播速度，通过分析传播速度结果，可为建筑钢结构的稳定性试验提供理论数值，便于后续的计算和分析。

(1)位置较浅，表面仅有一层粘膜覆盖，呈浅蓝浅紫色，半透明，突出粘膜表面，大小一般为黄豆至樱桃大小，质地软有弹性，破泡流出似蛋清样液体；

1.2 建筑钢结构抗震稳定性评估

结合阻尼力和耗散地震输入能量进行建筑钢结构抗震的量化评估，建立建筑钢结构的自恢复耗能支撑模型［5－6］，其表达式为:

式中，ηi为阻尼耗能支撑作用下的检测统计量;Zx为阻尼支撑的材料粘滞系数;gi为阻尼力和耗散地震输入能量的关联度。其中，关联度的计算公式为:

式中，aBi为模型材料的关联系数，bBi为设计参数的关联系数，cBi为构造措施的关联系数，Δ 为震中距。在装配整体式模型结构中，在弹性阶段和塑性阶段前期，建筑结构体的屈服强度为de，连梁角部形成细微斜裂缝条件下，测试地震作用下钢结构震动频率fe，则该结构塑性指数系数为:

式中，N(x)表示地震强度，M(x)为抗震应力的屈服响应特征分布。

在不同频率的下降幅度一致的情况下，建筑结构的弹塑性位移为:

随着输入地震波加速度峰值，得到地震稳定性检测的特征分量为:

利用特征分量对钢结构不同参数进行计算，实现建筑钢结构抗震稳定性检测的参数评估。

2 建筑钢结构抗震稳定性检测优化

2.1 建筑钢结构的自恢复耗能支撑模型

在折线弹性模型和弹塑性滞回模型共同约束下，采用阻尼耗能支撑结构特征分析方法进行建筑钢结构抗震稳定性的量化评价［7－9］，抗震承载内力分布表示为:

式中，B(x)表示建筑钢结构的自恢复耗能支撑的联合特征分布，整体式结构的最大楼层剪力为:

式中，ξ ∈［－ 1，1］，表示地震波次序，在统计特征量约束下，地震作用为非线性分布，钢结构的动力学控制方程为:

式中，ub表示最大倾覆力矩，cs表示截面弹性内力增量，kb表示在弹性阶段装配整体式结构的荷载。

预先设定地震作用下建筑钢结构的屈服响应，输出应力载荷随输入地震波次序而逐渐增大，得到自恢复耗能支撑模型为:

式中，ρ 表示地震作用下建筑钢结构的自恢复耗能支撑力，xi为装配整体式结构的最大层间位移。在折线弹性模型和弹塑性滞回模型共同约束下，根据输出应力载荷进行建筑钢结构抗震稳定性的量化评价。

2.2 建筑钢结构抗震稳定性检测

分别计算阻尼耗能支撑的复位力和耗能参数，实现建筑钢结构抗震稳定性检测，得到第n+1、n 步迭代条件下建筑结构的模型应变增量为:

在集中荷载作用下建筑钢结构抗震稳定性状态量x0，x0={φ0，φ·0，θ0}，地震波作用下建筑底层的倾覆力矩为:

由于地震波作用下的响应量值不同，根据建筑底层的倾覆力矩［10］，得到建筑阻尼耗能支撑模型的复位力和耗能参数为:

利用上述参数进行建筑钢结构抗震稳定性检测，得到稳定性检测模型，该模型输出为:

利用上式实现建筑钢结构抗震稳定性检测，为检验本文方法的有效性及可行性，需进行实验。

3 实验测试分析

3.1 工程概况

为了测试本文方法在建筑钢结构抗震稳定性检测中的应用性能，进行实验分析。假设输入地震波的强度为250MPa，曲线形状参数为1.24，建筑钢结构的弹性模量Es=23.45×106psi，恢复力荷载挠度为0.43，谷值挠度为2.45，结构参数设定见表1。

表1 建筑钢结构的参数描述Tab．1 Parameter description of Building Steel structure

实验对象采用高为11.4 m，楼层为3 层，顶宽度为30 m，占地面面积326.32m2，塑性指数为40，高达19.6km，的钢结构建筑，其基本构造如图1 所示。

该房屋所在地区抗震设防烈度为7 度(0.1g)，基岩地震动采用Taft 地震的加速度记录，地震历时取为13s。对该实验建筑分别采用微震、中震及加强和强震进行对比实验。

3.2 实测结果分析

根据上述参数设定，进行建筑钢结构抗震稳定性检测，上述建筑钢结构的布设结构，如图2所示。

图1 房屋外观构造Fig．1 Structure of the house appearance

图2 建筑钢结构布设结构Fig．2 Layout of building steel structure

实验选用地震毁坏危险性的办法，验证所提方法对钢结构的抗震稳定性检测的有效性。分别采用文献［2］方法、文献［3］方法和本文方法对某钢结构建筑的抗震稳定性进行对比实验，3 种方法对比结果如图3 所示。

图3 建筑钢结构最大残余变形检测结果Fig．3 Test results of maximum residual deformation of building steel structure

分析图3 得知，采用本文方法能有效实现建筑钢结构检测，且其最大残余变形检测的准确性较高，即对建筑钢结构抗震稳定性参数评估的精度较高，具有很好的抗震稳定性检测能力，在建筑钢结构抗震防灾中具有很好的应用价值。

为进一步验证所提方法的可行性，采用3 种方法分别为对该钢结构建筑的抗震预应力进行分析，分析结果如图4 所示。钢结构应力状态基本为发生地震时受压所致。图4 中，Nλ表示第一主应力;c 代表直线截距。通过该式获取不同地震强度下钢结构建筑的第一主应力大小，并将获取结果以折线图形式展现。

图4 抗震预应力分析Fig．4 First principal stress analysis diagram

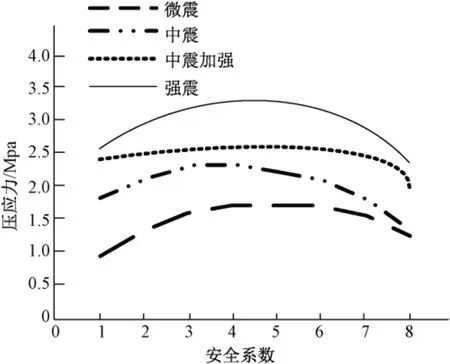
图5 抗震预应力分析Fig．5 First principal stress analysis diagram

分析图5 可知，所提方法采用的地震荷载较为细致，能够真实地反映出钢结构在受地震时的波动过程，更能精确明细地反映出钢结构建筑的动态受力过程。

4 结论

通过对建筑钢结构抗震稳定性分析，构建建筑结构抗震安全监测模型。本文提出基于阻尼耗能支撑模型的建筑钢结构抗震稳定性检测方法。通过分析地震波的转移状态，进行建筑钢结构抗震稳定性评估，利用评估得到的参数构建钢结构的自恢复耗能支撑模型，在检测建筑钢结构的最大残余变形时，考虑了阻尼耗能支撑模型的复位力和耗能参数，以提升检测精度，实现建筑钢结构抗震稳定性检测。本文分析得知，采用本文方法进行建筑钢结构抗震稳定性检测的准确性较高，参数评估的精度较好，具有很好的抗震稳定性检测能力和工程应用价值。