基于主成分分析和优化SVM 的公路边坡稳定性评价模型
牛鹏飞
(河北地质大学勘查技术与工程学院,河北 石家庄 050011)
0 引言
我国山区面积约占国土陆地面积70%。大量工程实践表明,在山区公路工程建设中,不良边坡体往往给公路工程的建设和维护带来不可预知的风险。因此,进行公路边坡稳定性评价具有重要意义。
公路边坡形成发育过程十分复杂,影响边坡稳定性的因素众多,各因素与边坡稳定性之间的关系是未知且非线性的,难以用一种简单的数学模型准确的反映出各因素之间的不确定、复杂关系。传统定性方法[1-4]评价边坡稳定性具有一定主观性,评价准确率较低。近几年,定量评价方法如BP 神经网络[5-7]、聚类分析法[8-9]、模糊综合评判法[10-11]等对边坡稳定性评价,取得一定成果,但也存在神经网络易陷入局部最优、聚类分析缺乏可比性、模糊评判结果出现超模糊现象等问题。
利用主成分分析法去除边坡稳定性影响因素的冗余属性,遗传算法优化支持向量机参数,支持向量机解决小样本数据以及非线性等实际问题中的优势[12],建立PCA-GA-SVM 的公路边坡稳定性评价模型。影响公路土质边坡稳定性的因素众多,选取容重、内聚力、内摩擦角、边坡角、边坡高度、孔隙水压力比6 个因素作为评价指标[13-14],通过主成分分析法对6 个因素进行分析,去除6个评价指标之间的关联性,重新线性组合出这些评价指标的主成分,作为遗传算法优化支持向量机模型的输入变量,通过模型应用于研究区训练样本及检验样本,以期解决因素之间复杂关系的问题,为公路边坡防治提供新思路。
1 PCA-GA-SVM 模型简介
PCA 是一种数学降维的方法[16],是设法将原来众多具有一定相关性的变量,重新组合成一组新的线性无关的综合变量来代替原来的变量。
GA 是模拟自然界生物进化机制的一种过程搜索最优算法[17],中心思想是对一定数量个体组成的生物种群进行选择、交叉、变异等遗传操作,最终求得最优解或近似最优解。
SVM 是一种二类分类模型[18],能够很好地处理小样本数据,具有高效、简便的分类、评价过程,是在特征空间上的间隔最大的线性分类器,并且能寻找到全局最优解。基本思想是求解一个能够正确划分数据集的分离超平面,并且保证这个超平面的几何间距最大化,对于线性可分的数据集,其最大几何间隔的超平面是唯一的。
PCA-GA-SVM 模型原理:通过PCA 分析法将影响公路边坡的一定相关性的因素,重新组合成新的线性无关变量,作为GA 优化SVM 模型的输入变量,以评价值作为输出变量,最终建立PCAGA-SVM 模型。
2 边坡稳定性评价模型的建立
2.1 公路边坡稳定性评价指标的确定
对文献[15]收集到的40 个边坡工程实例进行PCA-GA-SVM 评价模型的有效性检验。选取容重、内聚力、内摩擦角、边坡角、边坡高度、孔隙水压力比6 个因素作为影响边坡稳定性的因子。
在这40 个样本中随机抽取35 个样本数据作为训练样本(表1),剩余5 个作为检验样本(表2),用于验证所建立的基于PCA-GA-SVM 边坡稳定性评价模型的准确性。其中,边坡状态以1 和-1 来表示,1 代表“边坡稳定”,-1 代表“边坡破坏”。

表1 训练样本Tab.1 Training samples

表2 检验样本Tab.2 Testing Samples
2.2 主成分分析
为了更好地表示6 个影响因素之间的相关性关系,对表1 和表2 中的影响因素进行主成分分析,得到相关系数矩阵如表3 所示。由表3 可以看出,容重与内聚力、边坡高度都有较强相关性,孔隙水压力与内摩擦角有较强的相关性,内聚力与边坡高度之间也有较强相关性,当直接分析这些具有相关性的因素时,可能会出现严重的共线性问题。因此采用PCA 提取适当数量的主成分,并重新线性组合各评价指标,可以更清楚地阐述影响因素之间的关系。

表3 相关系数矩阵Tab.3 Correlation coefficient matrix

表4 公因子方差比Tab.4 Common factor variance ratio
表4 为各评价指标的公因子方差比。由表4 可知,除了内摩擦角有22. 2%的信息未被提取外,其它5 个评价指标的信息被提取得较充分。
表5 为计算标准化后的数据特征值和累计方差贡献率,其中F1……F6为6 个影响因素重新组合出的主成分。从表5 可以看出,前3 个主成分累计贡献率85.307%>85%,但是考虑到后续模型的预测效果,取前4 个主成分代表原来6 个变量所携带的信息。

表5 特征值及主成分贡献率Tab.5 Eigenvalues and principal component contribution rates
表6 为通过PCA 中最大方差法进行因子旋转,使因子载荷效果更加充分,得到的因子负荷矩阵。根据前4 个主成分在各影响因素下的权重系数可知,第一主成分中,系数绝对值比较大的影响因素为孔隙水压力、边坡角和内摩擦角,表明第一主成分主要反映的是孔隙水压力、边坡角和内摩擦角这3 个方面的信息。同理,第二主成分主要反映容重的信息,第三主成分主要反映内聚力的信息,第四主成分主要反映边坡高度的信息。

表6 因子负荷矩阵Tab.6 Factor load matrix
表7 为PCA 分析得到的因子得分系数矩阵。各评价指标可以通过该系数矩阵对各主成分重新进行线性组合,s1、s2、s3、s4、s5、s6分别代表容重、空隙水压力比、内聚力、边坡高度、内摩擦角、边坡角。得到4 个主成分(F1、F2、F3、F4)表达式见式(1)。
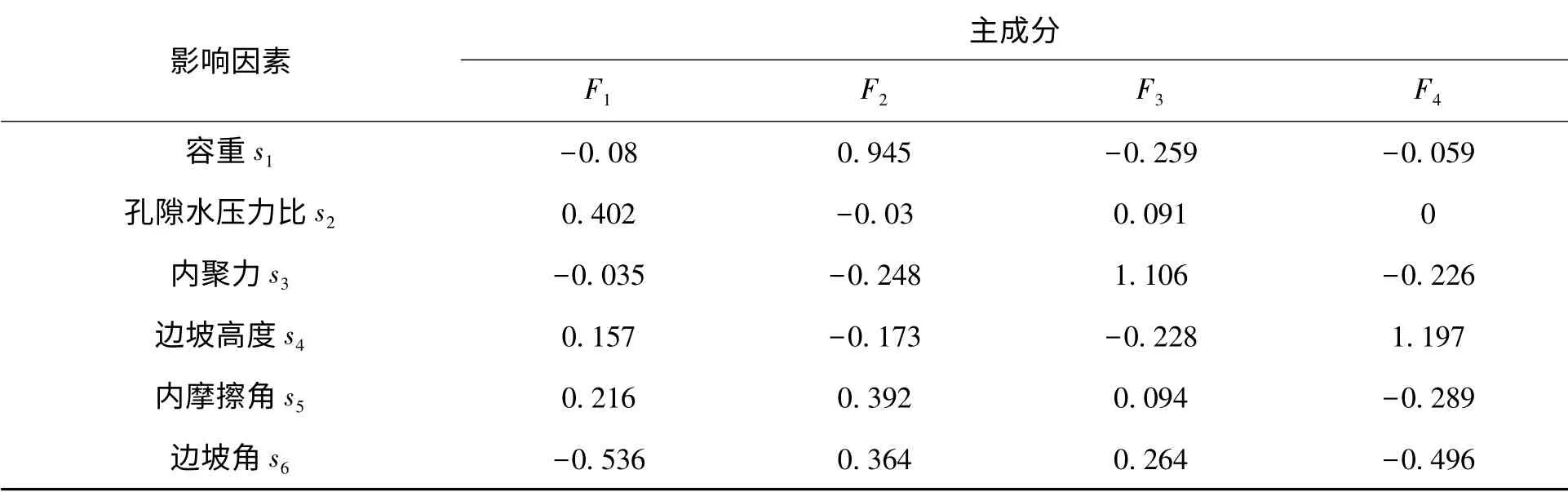
表7 因子得分系数矩阵Tab.7 Factor score coefficient matrix

由式(1),重新计算40 组原始数据样本的主成分,如表8 所示。把4 个线性无关的主成分作为支持向量机模型输入变量,既可以降低变量维数,也能够提高模型的运算效率。
2.3 遗传算法优化支持向量机模型
本文选择作为SVM 分类的核函数为径向基函数(RBF),并采用GA 算法确定核函数参数g和惩罚参数C。采用MATLAB 语言编写GA 优化SVM 模型参数程序,设置初始参数时,种群数量为20,进化代数为100,交叉率为0.8,变异率为0.2,经过多次训练寻找最优解,得到的最佳适应度曲线如图1 所示。
最优参数确定为C=6.7907,g=2.1315,均方误差MSE=0.059838,为检验PCA-GA-SVM 模型的可行性,运用主成分分析确定的4 个主成分(F1、F2、F3、F4)作为输入变量,对表1 中的训练样本数据进行回归仿真,训练样本的仿真回归值与实际值对比如图2 所示。

表8 原始数据样本的主成分Tab.8 Principal components of samples of raw data

图1 遗传算法寻优过程Fig.1 Optimization process of genetic algorithm

图2 PCA-GA-SVM 模型训练样本Fig.2 Training sample diagram of PCA-GASVM model
由图2 得知,基于PCA-GA-SVM 公路边坡稳定性评价模型对35 组训练样本的评价值与实际值非常接近,精度达到了工程要求,可以作为实际工作中评价模型。
2.4 结果与分析
通过PCA-GA-SVM 边坡稳定性评价模型对表2 中5 组检验样本进行评价,并与实际值进行对比,评价值与实际值的对比如图3 所示。为了检验主成分分析对预测结果的影响,表9 给出了PCA-GA-SVM 模型与GA-SVM 模型评价误差的比较结果。

图3 检验样本评价值和实际值对比Fig.3 Comparison between sample evaluation and actual values of testing samples

表9 评价值与实际值对比Tab.9 Comparison between evaluation and actual values
由图3 以及表9 结果可知,基于PCA-GASVM 模型的评价结果的最大绝对误差为0.0921,最大相对误差9.21%,而GA-SVM 模型的评价结果的最大绝对误差为0.1581,最大相对误差15.81%。可以看出PCA-GA-SVM 模型的评价结果在精度上要优于GA-SVM 模型,能够满足实际工程的需要。
3 结论
(1)影响边坡稳定性的因素众多,难以用一种常规简单的模型准确反映出各因素之间的不确定、复杂关系。本文通过建立PCA-GA-SVM 公路边坡稳定性评价模型,模型较好地解决了这一问题,进一步阐述了各因素之间的关系。
(2)引入主成分分析的降维思想,用4 个线性无关的主成分F1、F2、F3和F4表达了6 个影响公路边坡稳定性因素信息量的92.064%,提高了模型的计算速度和评价精度。
(3)通过对检验样本的评价,PCA-GA-SVM模型的最大相对误差为9.21%,评价结果与实际值较接近,精度优于GA-SVM 模型。因此PCAGA-SVM 模型可以在实际工程中应用,为公路边坡防治提供依据。

