基于流动因子的高压柱塞副往复密封性能研究

2 廖瑶瑶2 廉自生2

(1.太原理工大学机械与运载工程学院， 山西太原 030024； 2.煤矿综采装备山西省重点实验室，山西太原 030024)

引言

随着科学技术的进步，液压系统也向着压力高、速度快、流量大、可靠性高等方向发展，对液压密封元件的可靠性提出更高要求。往复密封元件不仅可以防止液压系统工作介质外泄造成环境污染，同时更可阻碍环境中粉尘等杂质进入液压系统。最近几十年中， 由于往复密封元件在液压系统可靠性、安全性等方面的重要作用，引起了国内外研究者的广泛关注[1-2]。

李强等[3]利用ANSYS对航空作动器O形密封圈的静态接触压力及von Mises应力进行了分析。欧阳小平等[4]采用流体动力逆解法，利用有限元仿真得到的静态接触压力近似等于流体压力，计算得到光滑表面往复密封泄漏量、摩擦力等。实践表明，往复动密封一般可形成不超过1～2 μm的油膜，油膜厚度与密封圈表面粗糙度同在微米或亚微米数量级。此时，密封圈粗糙度对往复密封性能起着重要作用。

综上所述，往复密封已有研究工作主要集中在利用有限元软件分析密封圈的静密封性能和采用流体动力逆解法计算其动密封性能，而对密封圈表面粗糙度效应和流体动压力与弹性变形的流固耦合作用对往复动密封性能研究较少。因此，基于流动因子的平均雷诺方程，建立了一种考虑密封圈表面粗糙度效应的弹流混合润滑模型。在ANSYS分析的基础上，利用MATLAB编程计算，研究了密封圈粗糙度对阶梯形组合密封的摩擦力、泄漏量和油膜分布等的影响，揭示了其往复密封机理，为往复密封结构设计与优化提供参考。

1 理论模型

1.1 密封圈弹性与接触力学分析

采用ANSYS对阶梯形密封的径向安装预压缩和流体压力的轴向压缩进行数值模拟。阶梯形密封由弹性O形圈和PTFE滑环组成，安装在缸套与柱塞杆之间，如图1所示。密封结构、载荷和边界条件均呈现轴对称特性，因此有限元分析简化为二维轴对称模型。

图1 阶梯组合密封示意图

数值仿真时，分两个载荷步施加。首先柱塞杆向上移动位移δ模拟安装时的径向压缩；其次，在O形圈流体一侧的非接触区施加均布载荷模拟流体压力的轴向压缩。图2a为有限元模型，图2b为加载后在柱塞杆与滑环之间形成的静态接触压力psc和接触长度L，为下一步计算动密封提供基础。

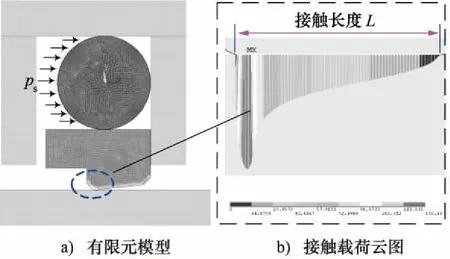
图2 密封圈安装加压示意图

1.2 流体力学

鉴于柱塞杆表面粗糙度大约是密封圈表面粗糙度的十分之一[5]，因此，只考虑密封圈表面粗糙度，柱塞杆为光滑表面，模型假设密封圈两侧充满油液。采用基于平均流动因子雷诺方程[5-7]，不仅可描述密封圈润滑的流体规律，还可表征粗糙度间的相互作用。

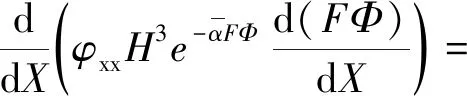
(1)

式中,φxx和φscx分别为压力流量因子和剪切流量因子[8]；F为空化因子；Φ为流体压力/密度函数，流体区域Φ≥0，F=1，P=Φ，空化区域Φ<0，F=0，P=0，P为无量纲流体压力。定义如下量纲一化变量：

U=μ0uL/paσ2，P=pf/pa，Ps=ps/pa

式中，x为轴向坐标；h为油膜厚度；σ为密封圈均方根粗糙度；α为压黏系数；pa为大气压力；hT为平均局部油膜厚度；μ0为常压流体黏度；u为往复速度；pf为流体压力；ps为密封压力。

边界条件：

(2)

假设密封表面粗糙度服从高斯分布，则：

(3)

1.3 微观接触力学

密封圈表面粗糙度间的相互作用采用Greenwood-Williamson接触模型来表示[9]:

(4)

(5)

式中，R为粗糙度半径；η为粗糙度密度。根据Streator[10]，定义如下量纲一化参数γ和β。

R=βσ

(6)

η=γ/R2

(7)

1.4 微弹性变形

油膜厚度相对密封圈源于安装和加压产生的径向变形非常小。因此利用小变形理论，密封区任一点的油膜厚度的变化等于接触区上其他载荷在该点引起的位移之和。则密封区任一点油膜厚度[5，7]：

(8)

式中，Hs为静态油膜厚度，把静态接触压力psc代入式(4)的线性回归得到；I为影响系数矩阵，采用ANSYS计算得到[5,7]。由于该润滑模型耦合了弹性变形、流体压力和粗糙度间的接触压力三部分，因此采用迭代解法求解上述方程，图3为计算流程图。

图3 计算流程图

计算得到求解上述方程组得到油膜厚度，流体压力和接触压力后，则可计算得到摩擦力和泄漏率，其中流体平均剪应力：

(9)

式中，φf,φfs,φfp为剪切流动因子[13]。

微凸峰接触剪应力:

(10)

其中，f为经验摩擦系数。则总摩擦力包含流体的黏性摩擦力和粗糙度微凸峰之间的接触摩擦力:

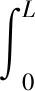
(11)

式中，D为柱塞杆直径。

泄漏率：

(hT+σ·φscx)

(12)

2 结果与分析

本研究选取如下计算参数[5,12]：阶梯密封O形圈Mooney-Rivlin参数C10=0.43295，C01=1.51508，d=0.001027，滑环弹性模量E=600 MPa，泊松比υ=0.4，柱塞杆直径D=25 mm，常压黏度μ0=0.0396 Pa·s，黏压系数α=2×108 Pa-1，β=1.75，γ=1，行程s=50 mm，密封压力ps=40 MPa，pa=0.1 MPa。

图4给出了高压柱塞副分别在内行程和外行程时静态接触压力psc、 粗糙度接触压力pc和流体压力pf

图4 压力分布曲线

的分布规律。由图可知，内外行程量纲一化油膜厚度H均小于3，密封接触面处于混合润滑状态。内行程中，流体压力从高压流体侧到低压空气侧逐渐减小，而粗糙度接触压力与静态接触压力呈现出相似的分布，先迅速增大，后逐渐减小到0。外行程中，粗糙度接触压力与静态接触压力相差很小，而流体压力基本为0。内行程中，粗糙度接触压力和流体压力共存，且粗糙度接触压力大于流体压力。结果表明，外行程时粗糙度接触摩擦力占主导作用，而内行程时尽管流体压力与粗糙度接触压力共同影响密封性能，但粗糙度接触剪应力对摩擦力起主要作用。同时可看到，内行程密封区接触长度大于外行程接触长度，原因是内行程高压流体作用下密封圈产生更大的形变所致。

高压柱塞副密封圈与柱塞的摩擦产生热量，引起能量耗散，降低系统机械效率。另外，密封圈与柱塞之间的泄漏降低了液压系统的容积效率，同时对环境造成一定污染。因此，研究高压柱塞副摩擦与泄漏机理，减小摩擦力和泄漏率成为提高液压系统效率的关键所在。

2.1 摩擦力

为研究密封圈表面粗糙度对其动往复密封性能的影响，本节给出了2种不同速度时，往复密封摩擦力随粗糙度的分析结果。图5给出了不同粗糙度密封圈在速度分别为u=0.6 m/s和1.2 m/s时的摩擦力。由图可得，内行程摩擦力Ffi随粗糙度的增大而增大，外行程摩擦力Ffo随粗糙度无明显变化。由此可见，减小密封圈粗糙度有利于降低其往复密封摩擦力。另外，外行程的摩擦力随粗糙度的变化曲线在两种不同速度时基本重合，进一步说明在外行程时，粗糙度摩擦力起主导作用，流体黏性剪应力引起的摩擦力可忽略不计。但在相同粗糙度的内行程中，速度增大得到较小的摩擦力，原因是内行程速度增大增强了流体动力效应，使得流体压力增大所致。在内行程中注意到，随着粗糙度的增大，由速度引起的摩擦力变化逐渐减小，当粗糙度大于3.5 μm时， 两个不同速度的内行程摩擦力基本相同。这说明，在内行程中由速度引起的流体动压效应随粗糙度的增大而逐渐减弱。

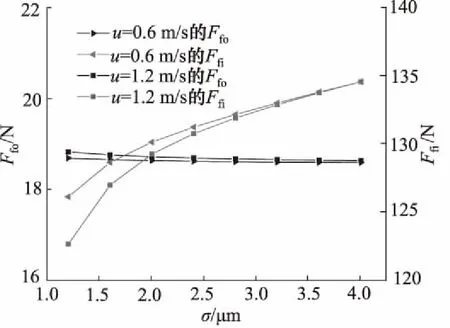
图5 两种不同速度下摩擦力随粗糙度变化曲线

2.2 泄漏量

如图1所示，在外行程时流体压力为低压，泄漏量Qo只有柱塞杆向外的速度引起的剪切流量。在内行程时流体处于高压状态，产生从高压侧到低压侧的压差流量，同时柱塞杆向内的速度产生向内的剪切流量，因此，在内行程中的泄流量Qi等于剪切流量减去压差流量。注意到，当内行程的泄漏量为负值时，代表外泄漏。一个往复的净泄漏量Qn等于外行程的外泄漏量减去内行程的内泄漏量。图6为u=0.6 m/s和1.2 m/s 两种不同速度时，往复密封一个行程中的内泄漏量，外泄漏量和净泄漏量随密封圈粗糙度的变化规律。由图可知，随着粗糙度的增大，内行程时正的内泄漏量减小，负的外泄漏量和净泄漏量增大，而外行程的泄漏量随着粗糙度的增大而略微增加。注意到，内行程泄漏量随着粗糙度的增加，在某一临界粗糙度σc

图6 泄漏量随粗糙度变化曲线

时泄漏量从正值转变为负值。当粗糙度σ<σc时，随着粗糙度的增大，内行程向内的剪切流量大于向外的压差流量，内行程泄漏量为正值，表现为越来越小的内泄漏；当粗糙度σ≥σc时，随着粗糙度的增大，内行程向内的剪切流量小于向外的压差流量，内行程泄漏量为负值，表现为越来越大的外泄漏。

由图6还注意到，速度不同时，得到不同的临界粗糙度，u=0.6 m/s和1.2 m/s时，其临界粗糙度分别在1.8 μm和2.6 μm左右。结果表明，不同的速度对应不同的临界粗糙度。为研究不同速度对应的临界粗糙度，图7给出了5种不同速度的内行程泄漏率随粗糙度的变化规律。由图得到，随着粗糙度的增大，内行程泄漏率经历了从正值到负值的转换，且随速度的增大，相同粗糙度时，内行程的内泄漏率随速度增加而增大，内行程外泄漏率随速度增大而减小。

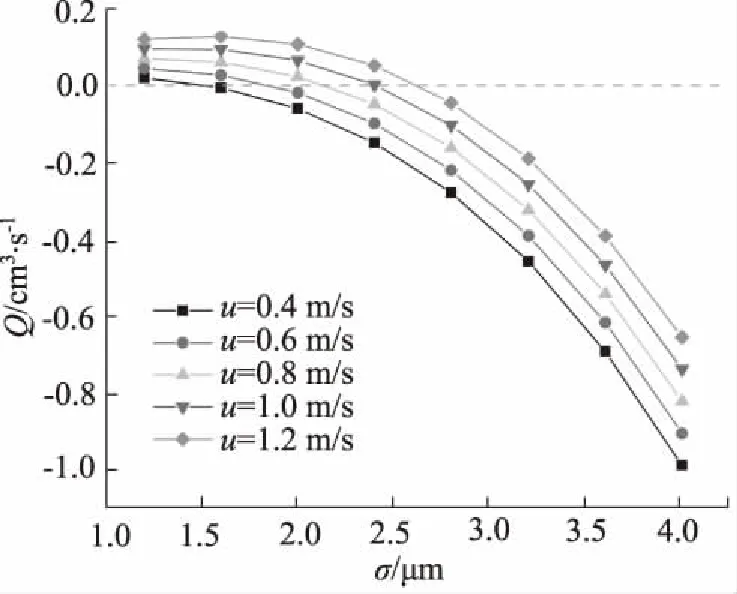
图7 不同速度内行程泄漏量随粗糙度变化曲线

图8给出了不同速度时的临界粗糙度。由图可看到，随着速度的增大，其临界粗糙度也增加。这说明速度增加引起的剪切流增加时，粗糙度增大引起的压差流量同时增大。因此，在流体压力一定时，增加密封圈粗糙度导致向外的压差流量增大。

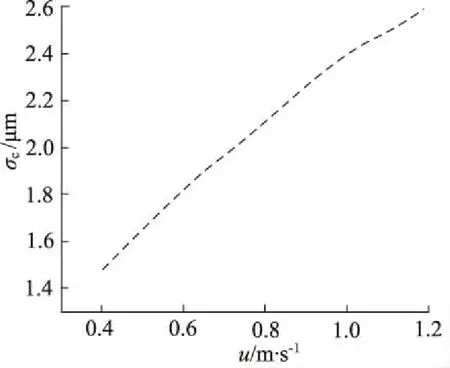
图8 不同速度的临界粗糙度

2.3 油膜厚度

为进一步研究密封圈粗糙度对油膜厚度的影响，加深对往复密封机理的理解，本节给出了不同粗糙度时油膜厚度分析结果。图9给出了u=0.6 m/s时，3种不同密封圈粗糙度的油膜厚度分布曲线。可以看到，随着粗糙度的增大，密封区平均油膜厚度呈现增大的趋势。而油膜越厚，泄漏量越大，这与2.2节得到的泄漏量随粗糙度的变化规律一致。同时可以看到，量纲一化油膜厚度在大部分密封区都小于3，说明往复密封区处于混合润滑状态，密封圈粗糙度对往复密封性能的影响不可忽略。同时，3种粗糙度下的量纲一化油膜厚度分布曲线几乎重合，从而表明粗糙度对量纲一化油膜厚度影响较小。

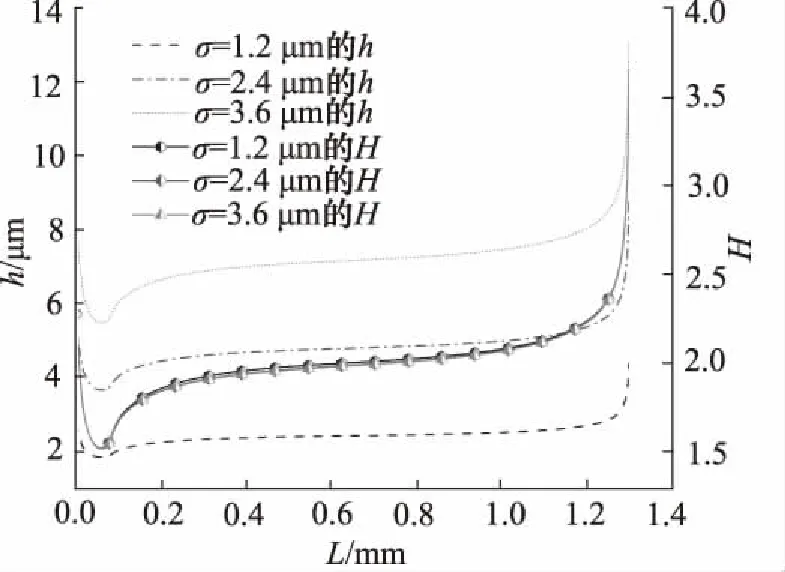
图9 不同粗糙度油膜厚度

3 结论

本研究利用ANSYS与MATLAB联合仿真的数值方法，建立了基于流动因子的阶梯往复密封弹流润滑模型，分析了密封圈表面粗糙度对往复动密封摩擦力、泄漏量和油膜厚度分布规律的影响，为工程密封结构设计与优化提供理论计算依据。主要得到以下结论：

(1) 往复动密封接触区处于混合润滑状态，摩擦力由流体引起的黏性摩擦力和粗糙度引起的接触摩擦力;

(2) 内行程摩擦力随粗糙度的增大而增大，外行程摩擦力随粗糙度无明显变化。在内行程，随着粗糙度的增大，由速度引起的摩擦力变化逐渐减小，当粗糙度大于3.5 μm时，两个不同速度的内行程摩擦力基本相同。这说明，在内行程中由速度引起的流体动力效应随粗糙度的增大而逐渐减弱;

(3) 随着粗糙度的增大，内行程泄漏量减小，但净泄漏量增加，而外行程的泄漏量随着粗糙度的增大而略微增加。存在某一临界粗糙度σc，当σ<σc时，随着粗糙度的增大，内行程向内的剪切流量大于向外的压差流量，内行程泄漏量为正值，表现为越来越小的内泄漏；当σ≥σc时，随着粗糙度的增大，内行程向内的剪切流量小于向外的压差流量，内行程泄漏量为负值，表现为越来越大的外泄漏。随着速度的增大，其临界粗糙度也增加；

(4) 随着粗糙度的增大，密封区平均油膜厚度呈现增大的趋势，而粗糙度对量纲一化油膜厚度无明显影响。