内爆炸准静态压力对球形容器弹塑性动态响应的影响
孙 琦,董 奇,杨 沙,张刘成
(中国工程物理研究院化工材料研究所,四川 绵阳 621999)
1 引言
爆炸容器作为一类特殊密封压力容器,可限制一定量爆炸物的爆炸效应,对容器内部的爆炸过程进行有效约束。在研究有限空间内爆炸准静态压力对结构响应的影响时[1-7],常常会使用爆炸容器、爆炸塔等设备进行爆炸试验和威力评估。爆炸容器按照设计准则可分为单次使用与多次使用两种类型。其中,单次使用型爆炸容器允许材料发生一定的塑性变形,但不能发生破坏;多次使用型爆炸容器的防护当量须把容器材料限制于弹性极限内,不能产生塑性变形。
Baker[8]针对薄球壳在内部三角脉冲冲击载荷作用下的动态冲击响应过程,提出了单自由度运动方程,获得了薄球壳受冲击载荷后的位移响应的弹性和双线性弹塑性解析解,但未考虑准静态压力的影响。Jones[9]同样利用单自由度模型对薄球壳的弹塑性动态响应过程进行了推导,获得了单一矩形脉冲作用下薄球壳的弹性-理想塑性、理想刚塑性响应解析解,但仅考虑弹塑性屈服发生于脉冲结束后的情况,未考虑屈服发生在脉冲作用阶段的情况。结合前人工作[8-9]与前期准静态压力对球壳弹性响应的影响研究[7],本研究提出考虑准静态压力的薄球壳双线性弹塑性动态响应的解析解,对前人工作进行了一定的补充和完善,并利用该方法研究了内爆炸准静态压力对球形容器弹塑性动态响应的影响。
2 力学模型分析
2.1 研究模型
基于之前对球壳在内爆炸载荷作用下弹性响应过程的研究[7],建立考虑准静态压力的简化载荷的表达如式(1)。
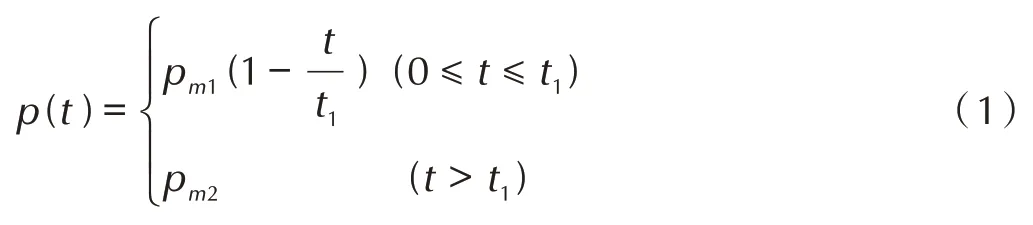
式中,pm1为首个脉冲压力峰值,t1为首个脉冲作用时间,pm2为准静态压力。当不考虑准静态压力时,令pm2=0 即可。
在承受来自容器中心的爆炸冲击载荷时,球形容器外壁各处应力应变状态相似,球壳的动态响应过程简化为在径向位移上的单一自由度受迫振动问题[8]。此情况下,由于冲击载荷沿径向分布作用于球壳内表面,因此可利用单自由度运动模型对动态响应过程进行分析,得出位移随时间变化的解析解。本研究与前期球壳弹性响应研究中使用相同尺寸的球壳模型[7],r为球壳中线半径,41 mm;h为壳体厚度,2 mm。并选用如图1 所示的等向强化的双线性弹塑性材料,其材料属性如下:E为弹性模量,200 GPa;Et为切线模量,10 GPa;σs为屈服强度,200 MPa;v为泊松比,0.3;ρ为密度,7830 kg·m-3;图1 中σ和ε表示应力和应变,σs和εs为屈服应力和应变,σmax为球壳径向位移达到最大值时的应力。

图1 等向强化的双线性弹塑性模型Fig.1 Biolinear elastic-plastic model with isotropic hardening
2.2 响应过程分析
前期研究中,已得到弹性状态下球壳受考虑准静态压力冲击载荷作用时的动态响应的解如式(2)[7]。
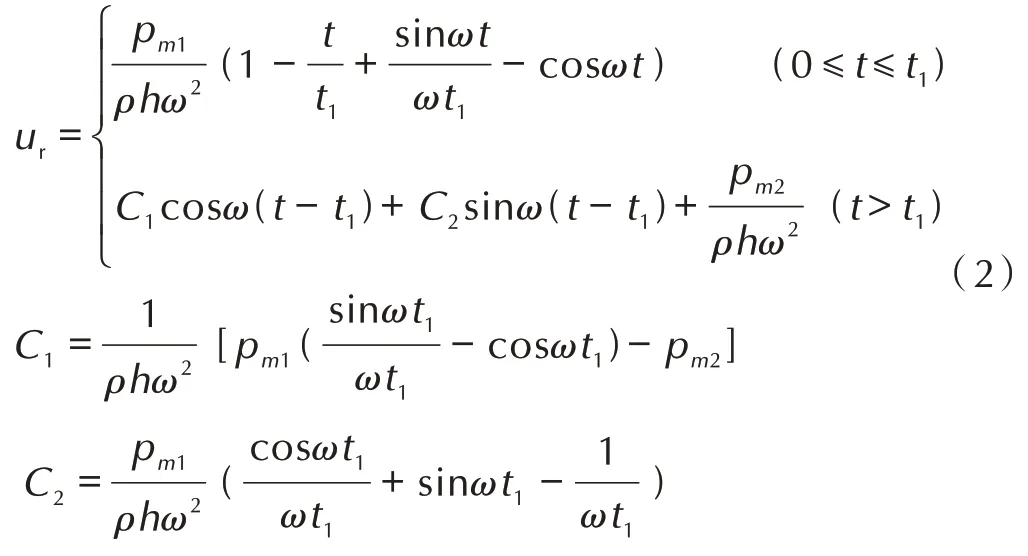
式中,ω为振动频率,振动周期T=2π/ω。
在进入塑性阶段后,球壳表面仍有σθ=σφ=σ,应力可表示为:

故球壳受内部冲击载荷时,进入塑性阶段后单自由度运动方程应表示为[8]:

设屈服发生时刻为ts,则有如下两种分析情况。
(1)屈服发生于首个脉冲阶段,即0<ts<t1
a.在弹性段,式(2)仍然适用,直至应力σ达到屈服应力σs,此时0<t≤ts。
b.当ts<t≤t1时,设t′=t-ts,将初值条件式(5)代入塑性阶段SDoF 方程式(4)可解得该阶段位移响应的解如式(6)。

c.当t>t1时,设t″=t-t1,式(4)可简化为式(7)
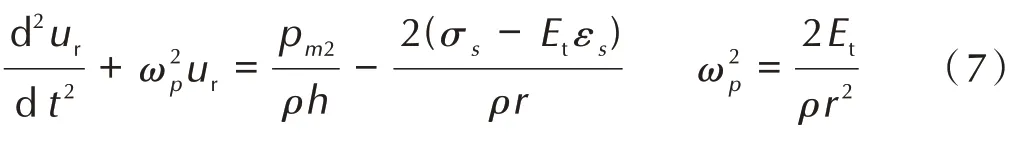
代入初值条件式(8)可得该阶段位移响应的解如式(9)。
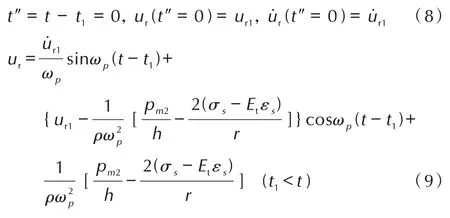
(2)屈服发生于准静态压力作用期间,即ts≥t1
a.当0<t≤t1时处于弹性段,位移响应的解适用式(2);
b.当t1<t≤ts时处于弹性段,式(2)仍然适用,直至应力σ达到屈服应力σs;
c.当t>ts时,设t‴=t-ts,塑性阶段SDoF 方程式(4)同样可以简化为式(7),将初值条件式(10)代入可解得该阶段位移响应的解如式(11)

需要注意的是,两种情况中当位移响应达到最大值后回弹的过程,成为弹性等幅振动过程。设首个位移响应最大值出现时刻为tmax,位移最大值为urmax,则后续弹性等幅振动的运动方程满足弹性情况下的SDoF 运动方程[8],其初值条件为t=tmax,ur(tmax)=
3 数值模拟校验
本研究中使用LS-DYNA[10]对球壳内部冲击载荷下的弹塑性动态响应过程进行数值模拟,并与解析解结果进行对比。本研究中使用的有限元模型与弹性响应研究中的1/8 球壳模型[7]相同,但材料属性设置为MAT_PLASTIC_KINEMATIC,并在K 文件中设置BETA=1 表示等向强化,材料参数如2.1 所示。冲击载荷按照简化载荷曲线式(1)进行定义,计算时长150 μs,计算步长0.1 μs。
假定三种不同冲击载荷Load 1~Load 3 见表1,其中Load 1 情况下最大位移出现于准静态压力阶段,Load 2、Load 3 情况最大位移出现于首个脉冲阶段,代入解析解公式进行计算。将计算得到的动态响应过程特征值,如最大位移出现时刻、最大位移值和振幅,与LS-DYNA 数值模拟结果进行对比验证。载荷Load 1~Load 3 的对比结果如图2 和表2 所示。图2中ur为径向位移,mm;表2 中tmax为达到径向最大位移时刻,μs;urmax为径向最大位移值,mm;amplitude 为后续阶段振幅,mm;εr为理论解与数值模拟结果的相对误差。可以发现解析解公式与LS-DYNA 数值模拟结果符合情况较好,公式的准确性得到了数值模拟的验证。

表1 冲击载荷算例Table 1 Examples of impulsive loading
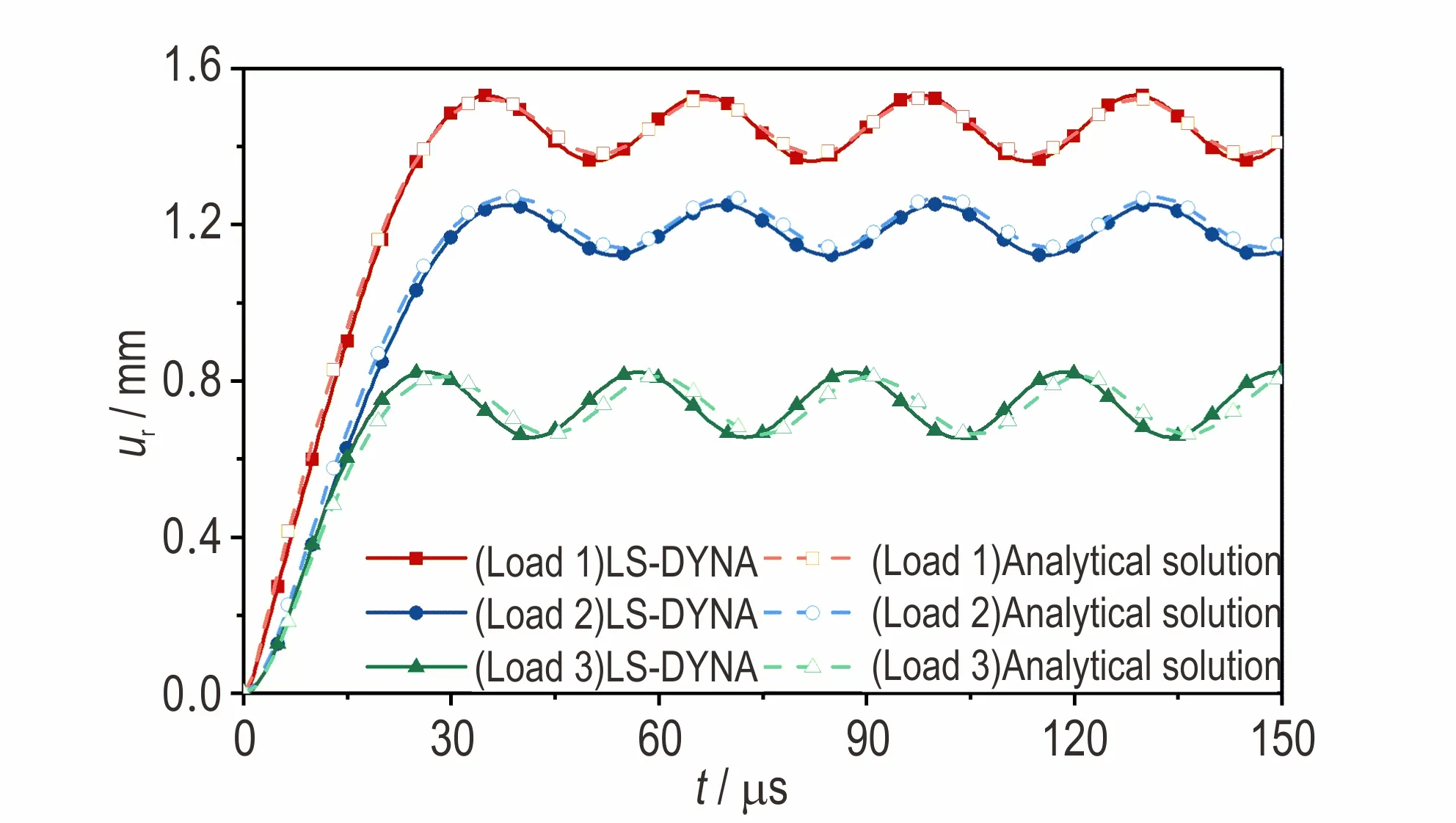
图2 位移响应解析解与LS-DYNA 数值模拟结果对比Fig.2 Comparison between analytical solution and LS-DYNA simulation
4 准静态压力的影响
参照前期研究[7,11],利用解析解分析准静态压力对球壳弹塑性动态响应过程的影响。在图3~图7 中,urmax指整个响应阶段位移最大值,amplitude 指塑性卸载后弹性振动的振幅值,urmin为后续弹性振动中位移最小值。表3、表4 为各算例中屈服时刻ts,首个最大位移出现时刻tmax,最大位移值urmax,后续弹性振动阶段振幅值amplitude 的计算结果。

表2 解析解结果与LS-DYNA 数值模拟结果对比Table 2 Comparison between analytical solution and LS-DYNA simulation
4.1 屈服发生于三角脉冲阶段
在保证首个脉冲冲量不变的情况下,针对屈服时刻发生于首个脉冲作用期间的情况,进行了图3~图5中pm1=400 MPa,t1=5 μs、pm1=200 MPa,t1=10 μs 和pm1=100 MPa,t1=20 μs 三种情况在不同准静态压力pm2水平下的分析。图3a、图4a 和图5a 表示不同载荷情况在pm2=0、30、60 MPa 三种准静态压力下计算得到的位移响应曲线,图3b、图4b 和图5b 则是将pm2作为变量,得到ur=ur(pm2)形式下径向位移响应最大值、塑性卸载后弹性振动位移最小值和振幅值关于pm2变化的曲线。
算例结果(图3~图5 和表3)显示,在不同准静态压力幅值下,屈服时刻不受准静态压力影响,最大位移出现在准静态压力段,随着准静态压力的增大,最大位移出现时刻变大;最大位移幅值受到准静态压力的影响,随着准静态压力幅值的增大而增大;后续弹性振动阶段位移最小值受准静态压力影响也较为显著,随准静态压力幅值的增大而增大。

图3 位移响应曲线及不同准静压的关键计算参数(pm1=400 MPa,t1=5 μs)Fig.3 Dynamic response and key calculated parameters at different quasi-static pressure(pm1=400 MPa,t1=5 μs)

图4 位移响应曲线及不同准静压的关键计算参数(pm1=200 MPa,t1=10 μs)Fig.4 Dynamic response and key calculated parameters at different quasi-static pressure(pm1=200 MPa,t1=10 μs)
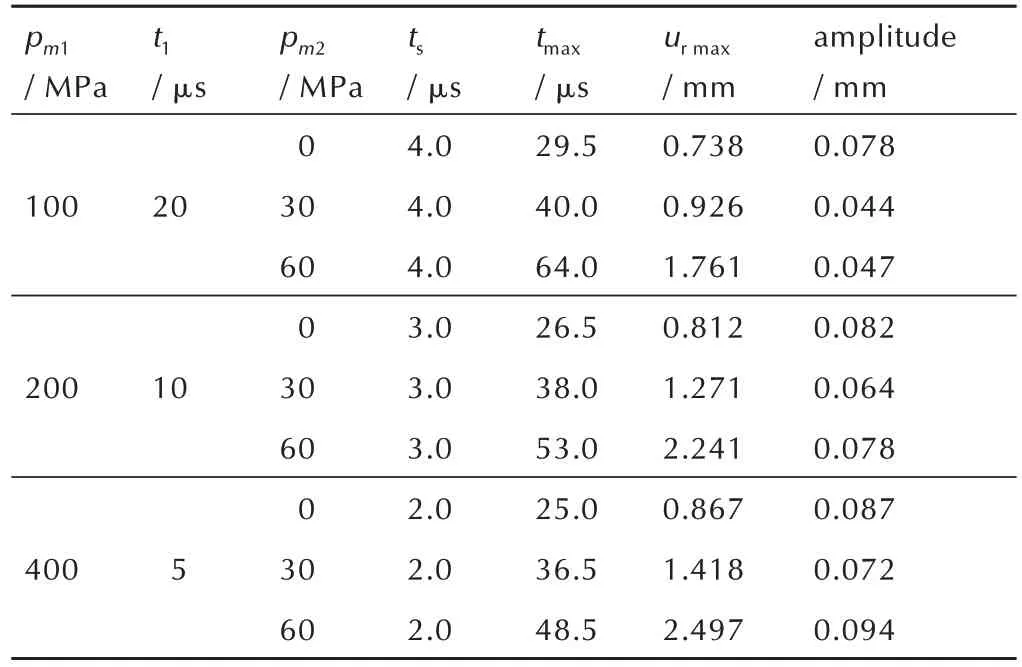
表3 屈服发生于三角脉冲阶段动态响应的参数计算值Table 3 Dynamic response parameters of yielding occurring in triangle impulse
4.2 屈服发生于准静态压力阶段
在首个脉冲冲量作用时间t1较小的情况下,屈服时刻发生于准静态压力作用期间,进行了如图6、图7中pm1=800 MPa,t1=2.5 μs 和pm1=400 MPa,t1=2.5 μs两种情况在不同准静态压力pm2水平下的分析。图6a、7a 表示不同载荷情况在pm2=0、30、60 MPa 三种准静态压力下位移响应曲线,图6b、7b 为径向位移响应最大值、塑性卸载后弹性振动位移最小值和振幅值关于pm2变化的曲线。

图5 位移响应曲线及不同准静压的关键计算参数(pm1=100 MPa,t1=20 μs)Fig.5 Dynamic response and key calculated parameters at different quasi-static pressure(pm1=100 MPa,t1=20 μs)

表4 屈服发生于准静态压力阶段动态响应的参数计算值Table 4 Dynamic response parameters of yielding occurring in quasi-static pressure phase
算例结果(图6~图7 和表4)显示,由于屈服发生于准静态压力阶段,屈服时刻会受到准静态压力幅值影响,随准静态压力的增大而减小;除此之外的结果与屈服发生于三角脉冲阶段情况类似,最大位移出现在准静态压力作用期间,其出现时刻随着准静态压力的增大而变大,最大位移幅值随准静态压力幅值的增大而增大;后续弹性振动阶段位移最小值受准静态压力影响较为显著,随准静态压力幅值的增大而增大。
与前期获得的弹性响应结果[7]相比较,弹性响应和弹塑性响应结果的不同之处主要表现为弹塑性响应分析中,准静态压力幅值对最大位移的影响更为显著;采用与前期研究[7]中类似的能量分析方法可以发现,弹性响应和弹塑性响应中,在后续阶段即使准静态压力作用时间很长、输入冲量很大,但后续振动阶段的最大变形幅度不受准静态压力影响。

图6 位移响应曲线及不同准静压的关键计算参数(pm1=800 MPa,t1=2.5 μs)Fig.6 Dynamic response and key calculated parameters at different quasi-static pressure(pm1=800 MPa,t1=2.5 μs)

图7 位移响应曲线及不同准静压的关键计算参数(pm1=400 MPa,t1=2.5 μs)Fig.7 Dynamic response and key calculated parameters at different quasi-static pressure(pm1=400 MPa,t1=2.5 μs)
5 结论
本研究获得了考虑准静态压力的内爆炸载荷作用下等向强化双线性弹塑性球形容器动态响应过程的分析模型和解析解,并得到了数值模拟结果的验证。通过对结构响应过程进行分析,获得了准静态压力对球形容器弹塑性动态响应的影响。研究结果表明:
(1)若屈服发生于准静态压力阶段,屈服时刻会受准静态压力幅值影响,随准静态压力的增大而减小。无论屈服发生于哪个阶段,在不同准静态压力幅值下,最大位移出现时刻均有明显差异,最大位移值随着准静态压力幅值的增大而显著增大。
(2)弹性响应[7]和弹塑性响应中,后续阶段即使准静态压力作用时间很长、输入冲量很大,但后续振动阶段的最大变形幅度并不受影响,即准静态压力幅值大小对响应过程起主要作用,而非准静态压力的总冲量或作用时长。弹塑性响应过程中准静态压力幅值对最大位移的影响更为显著。在炸药的威力评估工作中,针对准静态压力效应采取结构弹塑性响应分析更有实用价值和指导意义。

