双立柱堆垛机立柱动态挠曲变形分析
薛成超,付存银
(沈阳新松机器人自动化股份有限公司 智能物流BG,辽宁 沈阳 110168)
巷道堆垛机是自动化立体仓储系统的核心装备[1].堆垛机的性能指标直接影响仓储系统的效率、可靠性及运营成本.双立柱巷道堆垛机具有结构刚性大、适于高速重载的特点[2-3].对于堆垛机而言,载货台和货物对立柱的弯矩作用、堆垛机加减速产生的水平惯性力及不同的速度控制方式,都会对立柱动态挠曲变形产生影响[4-5].双立柱巷道堆垛机的门架结构属于超静定结构[6].目前,对双立柱堆垛机立柱挠曲变形的研究,主要参考吉国宏(日)所提出的力学模型,采用结构力学的角变位法中的立柱挠曲变形公式进行分析[7-8].吉国宏力学模型对堆垛机的下横梁进行简化,忽略了下横梁由自重、有效载荷、惯性力等因素导致的变形对立柱挠曲变形的附加影响.本文采用结构力学中关于超静定门架结构的角变位法,考虑下横梁变形,根据叠加原理[9]得到双立柱堆垛机立柱的动态挠曲变形公式.同时,采用有限元方法[10]计算立柱变形,并与挠曲变形公式的计算结果进行对比,以期修正原有双立柱堆垛机立柱挠曲变形计算模型,完善堆垛机立柱挠曲变形的计算方法.
1 双立柱动态挠曲变形模型
1.1 吉国宏双立柱动态挠曲变形模型分析
根据文献[7],双立柱堆垛机立柱受力分析模型如图1所示.
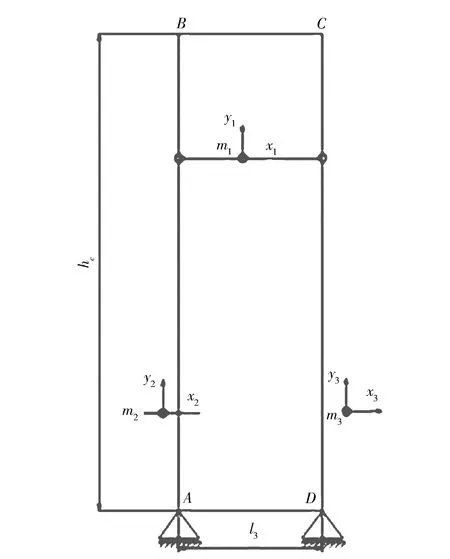
图1 双立柱堆垛机立柱受力分析模型
在文献[7]采用角变位法得到的立柱变形公式中,右侧立柱在惯性载荷与结构载荷作用下的受力平衡方程为:
(1)
左侧立柱在惯性载荷与结构载荷作用下的受力平衡方程为:
(2)
对式(1)和式(2)整理可得:
(3)
(4)

立柱挠曲变形为:
δ=Rhc=(R′+R″)hc
(5)
堆垛机立柱变形模型参数如表1所示.

表1 堆垛机立柱变形模型参数
在上述力学模型与变形公式中,未充分考虑有效载荷、惯性力等因素引起的下横梁变形而导致的立柱附加变形.
1.2 改进的双立柱动态挠曲变形模型分析
改进的双立柱挠曲变形分析模型如图2所示.
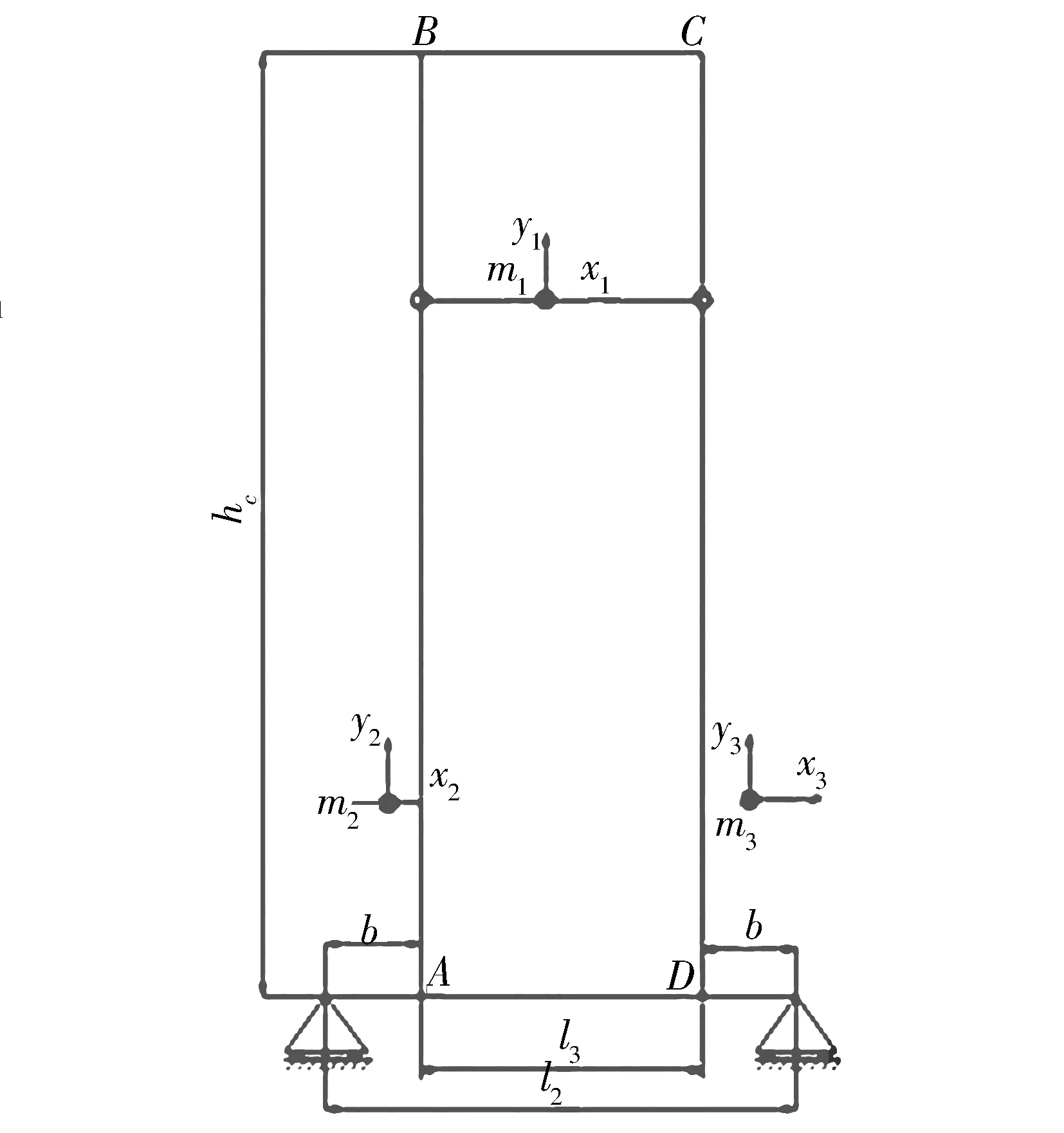
图2 改进的双立柱堆垛机立柱受力分析模型
对于该模型,采用角变位法[8]建立的右侧立柱倾角变位方程如下:
(6)
按文献[10]建立的节点平衡方程如下:
(7)
由上述各式求解可得:
(8)
(9)
(10)
式中:
对于改进的双立柱堆垛机立柱受力分析模型,采用角变位法建立的左侧立柱倾角变位方程如下:
(11)
所建立的节点平衡方程如下:
(12)
由上述各式求解可得:
(13)
(14)
(15)
式中:

引入改进双立柱挠曲分析模型中A点与D点载荷对立柱变形产生的影响后,求解的节点A、D处载荷如下:
(16)
(17)
(18)
(19)
式中:
由节点A处载荷导致的下横梁对应转角为:
(20)
由节点D处载荷导致的下横梁对应转角为:
(21)
双立柱堆垛机的立柱挠曲变形为:
(22)
式中:
2 双立柱动态挠曲变形模型求解与仿真分析
2.1 双立柱动态挠曲变形模型求解
分析式(22)可知,影响双立柱堆垛机立柱动态挠曲变形的因素主要为堆垛机的水平运行速度.
堆垛机双立柱动态挠曲变形的仿真参数如表2所示.
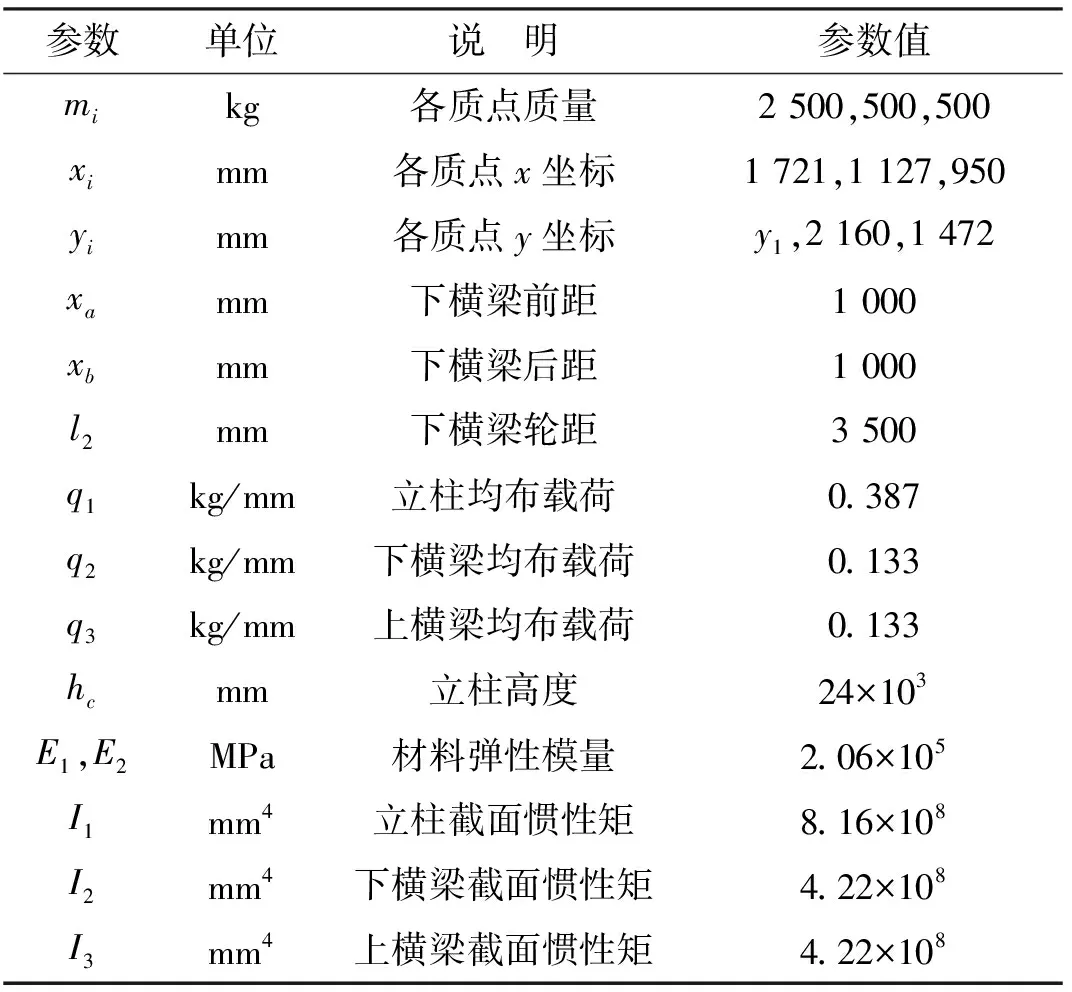
表2 堆垛机双立柱动态挠曲变形的仿真参数
根据表2中参数,将提升高度y1转换为提升运行时间t的函数,可得C与提升运行时间t的关系曲线(图3).

图3 C与提升运行时间t的关系曲线
2.2 仿真分析
利用APDL参数化编程语言[10],对双立柱堆垛机采用梁杆单元beam4进行建模.图4所示为双立柱堆垛机的立柱ANSYS模型和变形.
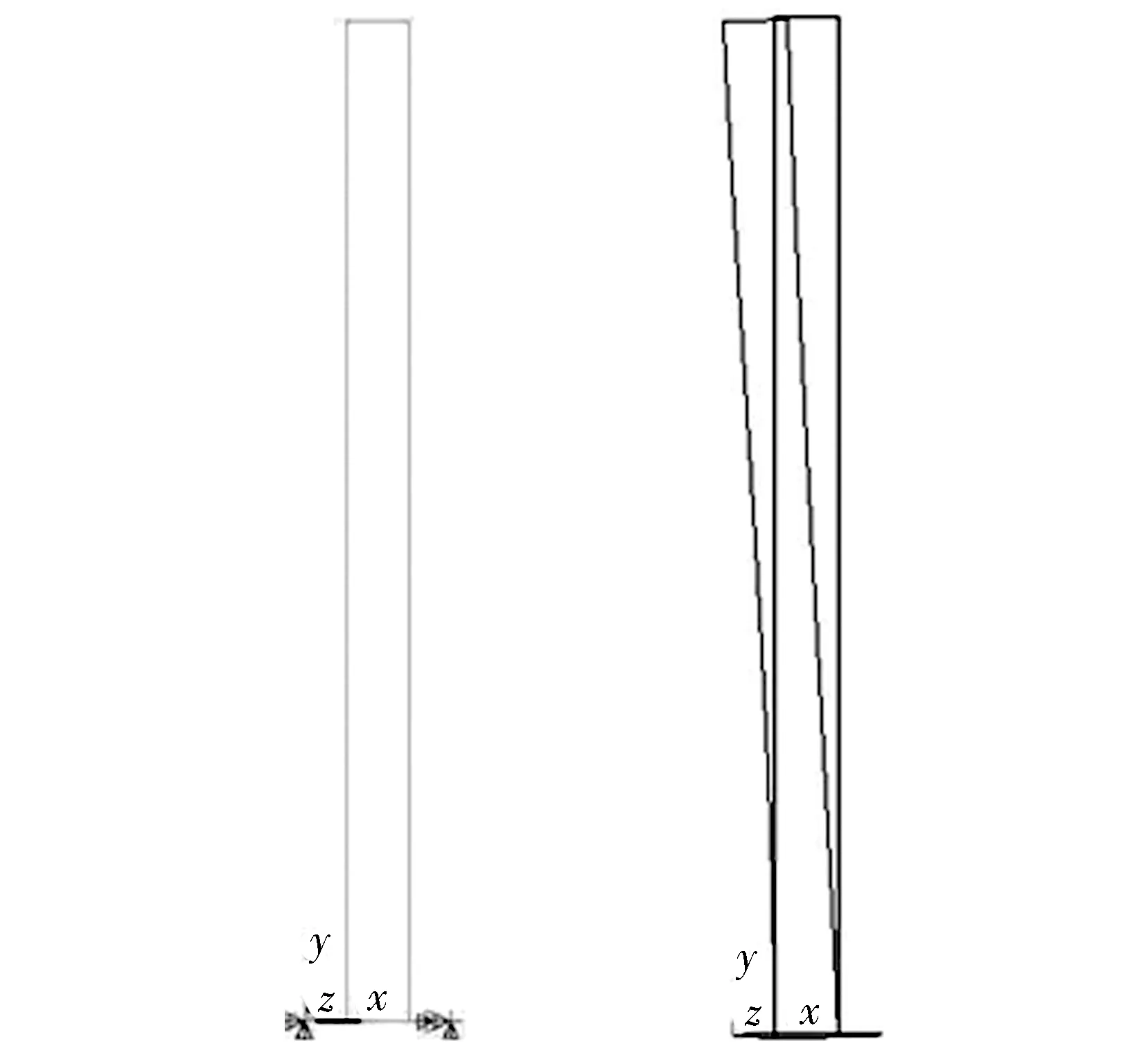
(a)ANSYS模型 (b)变形
对双立柱动态挠曲变形模型求解与仿真分析可得如下结果:原模型的挠曲变形为16.7 mm;改进模型的挠曲变形为18.1 mm;ANSYS模型的挠曲变形为17.5 mm.显然,改进模型的结果偏大.改进模型考虑了下横梁由自重、有效载荷、惯性力等因素导致的变形对立柱变形的附加影响,其结果与原模型相比偏大.但通常情况下,可将双立柱堆垛机视为轴对称结构,这种对变形的附加影响是有限的.
3 结 论
(1)采用结构力学中关于超静定门架结构的角变位法,考虑下横梁变形因素对立柱变形的影响,根据叠加原理得到了双立柱堆垛机立柱的动态挠曲变形公式.
(2)采用Matlab软件分别建立双立柱堆垛机两种立柱变形模型的计算程序,得到在同等结构与载荷条件下两种不同模型的立柱变形.采用APDL参数化编程语言建立双立柱堆垛机的简化ANSYS模型,计算了相应的变形结果
(3)对双立柱动态挠曲变形的原模型、改进模型和ANSYS模型的结果分析可知,改进模型考虑了下横梁变形因素对立柱变形的附加影响,其结果与原模型相比偏大,与ANSYS结果较为接近,同时该结果在工程设计中偏于安全.

