福州市平面坐标转换模型估计算法研究
吴建
(福州市勘测院,福建 福州 350108)
1 引 言
平面坐标系统是城市各项测量工作的基准,是城市最为重要的测绘基础设施。从20世纪50年代起我国开始采用经典大地测量技术建立全国性的平面坐标系统“1954北京坐标系”,到当前采用现代空间测量技术建立的各类高精度国家和城市坐标系统。福州市目前采用如下6套坐标系统:CGCS2000坐标系、WGS84坐标系、福州地方坐标系、福州大都市坐标系、1980西安坐标系以及1954北京坐标系,6套坐标系之间的转换是福州市测绘数据生产和应用的基本内容之一。坐标转换平差模型的系数矩阵包含坐标转换公共点在源坐标系下的坐标值,因而含有随机误差,不满足高斯-马尔科夫模型的假定条件,属于EIV(Errors-in-variables)平差模型。目前,福州市平面坐标系转换算法忽略了系数矩阵误差,基于经典的最小二乘估计求得的转换参数有偏[1]。Xu等(2014)[2]、曾文宪(2013)[3]从理论上研究了系数矩阵误差对最小二乘参数估计偏差以及参数精度的影响。Schaffirn(2008)[4]、Xu(2012)[5]、Shen(2013)[6]、Fang(2013)[7]等研究了整体最小二乘估计算法,姚宜斌(2010)[8]、方兴(2014)[9]等研究了坐标转换模型的整体最小二乘(Total Least-squares,TLS)估计算法。坐标转换模型的TLS估计具有渐进无偏性,理论上要优于LS估计。TLS估计属于非线性估计,计算复杂度远高于LS估计,实际应用中往往需要根据EIV模型系数矩阵误差对LS参数解以及参数精度的影响程度确定估计算法。当系数矩阵误差影响小能够满足精度要求时,可忽略系数矩阵误差采用LS算法求解;当系数矩阵误差对LS接的影响过大,则必须采用TLS估计算法求解。本文将利用EIV模型及其估计理论的最新研究成果,分析和评估了福州市平面坐标转换模型采用最小二乘估计(leastsquares,LS)引起的参数估计值的偏差以及对参数精度的影响;在此基础上,提出了福州市实际应用中平面坐标转换模型估计算法的选择方案和建议。
2 平面坐标转换模型的LS估计算法
平面坐标转换模型也称为四参数模型,对于第i个坐标转换点,模型形式如下:
(1)

若令c=mcosα,d=msinα,平面坐标转换平差模型可表示为:
l=(A-EA)β+el
(2)


相应的随机模型为:
(3)
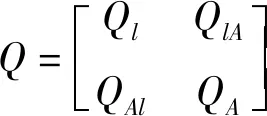

(4)
式中,P表示l的权阵。
3 福州市平面坐标转换模型LS估计偏差分析
3.1 坐标转换模型LS估计偏差公式
坐标转换模型属于典型的EIV模型,Markovsky(2007)[1]等证明了EIV模型的LS估计为有偏估计。测量领域,Xu(2013)[5],曾文宪(2013)[3]首次研究了EIV模型的LS估计偏差理论,以下笔者利用文献[3]中的理论从数值方面分析当前福州市平面坐标转换模型采用LS估计引起的估计偏差的数量级大小,以及系数矩阵误差对LS估计精度的影响。
如果忽略系数矩阵中的误差EA,根据文献[3],式(4)的LS参数估计偏差以及参数协方差阵估计偏差分别为:
(5)
(6)

(7)
式中,W表示系数矩阵中观测值对应的权阵。
3.2 福州市平面坐标转换模型LS估计偏差分析
实际测量工作中,福州市各级控制网的距离从数公里至数百公里,不同距离长度的控制网在进行坐标转换时LS估计的偏差的量级不同。为了涵括坐标转换各类情况,笔者设计了均匀分布的坐标转换点,如图1所示,且控制网点间距离分别为 5 km、10 km、50 km和 100 km等4类情况进行偏差分析。坐标转换数据精度涉及以下两种情况:
①现代坐标系统之间的转换(如WGS84与CGCS2000),观测向量l和系数矩阵精度均为厘米级,根据福州市实际情况均取 0.02 m;
②现代坐标系与经典大地坐标系之间的转换(如WGS84与1980西安坐标系),观测向量l的精度为厘米级,取 0.02 m;系数矩阵中的坐标值精度为分米级,取 0.2 m。自然资源部于2019年1月1日起不再提供1980西安坐标系以及1954北京坐标系下的测量成果,且各部门成果也要求转换到CGCS2000坐标系下,因此,经典坐标系之间的转换很少,这里不进行讨论。

图1 福州市域高等级控制点分布图


福州市Ⅰ类平面坐标转换模型LS估计偏差 表1


福州市Ⅱ类平面坐标转换模型LS估计偏差 表2
从表1和表2的实例数据分析,可以得到如下结论:
(1)坐标转换模型中,平移参数T的系数矩阵是固定阵,T的偏差和中误差与坐标网公共点间的距离(或系数矩阵的信噪比)无关,而旋转参数R和尺度因子S的偏差随公共点间的距离的减小约呈现二次方增长,中误差随距离的减小大致成比例减小,与前文理论分析一致。
(2)大地坐标转换模型中网距离通常在数公里以上,不论是第Ⅰ类现代大地坐标系之间的转换,还是第Ⅱ类现代大地坐标系和经典大地坐标系之间的转换,系数矩阵误差引起的LS参数估计值的偏差完全可以忽略不计。
(3)系数矩阵误差对参数精度的影响,要视坐标网大小、网形结构等而定。表中结果清楚地说明论文大地坐标转换模型用LS方法计算的参数中误差远小于中误差的实际值,即高估了坐标转换参数LS解的精度。在第Ⅰ类现代大地坐标系之间的转换中,由于观测向量中的目标坐标系坐标值和系数矩阵中的源坐标系坐标值精度相当,LS计算的参数中误差约只有实际值的50%。在第Ⅱ类现代大地坐标系和经典大地坐标系的转换中,由于经典坐标值仅为现代坐标系的坐标值精度的10%,LS参数精度更是高估。
(4)大区域范围进行坐标转换参数的解算时,若选择的坐标点分布均匀,当坐标网较大时(实例中坐标网的距离大于 100 km),LS估计能够满足精度估计要求。
4 福州市平面坐标转换模型估计算法选择建议
平面坐标转换模型属于系数矩阵含随机误差的EIV模型,最小二乘估计有偏。根据本文的理论和实证分析,对实践中福州市各类平面坐标转换模型参数估计算法提出如下建议:
(1)福州市平面坐标转换模型估计能否采用最小二乘算法,取决于式(6)计算的LS参数的方差或者中误差的大小,如果中误差在精度要求范围之内,则采用LS求解,但参数的中误差须按式(6)计算,经典的LS参数中误差公式由于没有考虑系数矩阵误差,不能反映其精度。如果参数的LS估计精度不能满足要求,则必须采用整体最小二乘估计算法求解坐标转换参数。
(2)从本文3.2对福州市各类坐标转换估计算法的实验分析来看,对于福州市现代大地坐标系统间的转换(第Ⅰ类),当公共点网距离在 50 km以上的较大区域计算平面坐标转换参数时,可忽略系数矩阵误差,采用最小二乘估计求解,完全可以满足当前高精度定位中坐标转换参数精度的要求。当公共网点距离 10 km以上时,如果公共点数量较多、网形合理以及分布均匀时,采用LS估计求解转换参数能够达到厘米级的定位精度要求。当公共网点距离在 10 km以下时,应视具体项目坐标点位精度要求、坐标网点距离、网形结构等确定LS估计能否满足精度要求。
(3)对于福州市现代大地坐标系与经典大地坐标系间的转换(第Ⅱ类),由于系数矩阵的精度约为分米级,因此,忽略系数矩阵误差得到的坐标转换参数的精度比第Ⅰ类数据约降低了一个数量级,表2反映了坐标转换参数的LS解的中误差主要来源于系数矩阵坐标值的误差。如果采用LS估计坐标转换参数,能满足分米级的坐标计算要求,同样,参数中误差应采用式(6)计算。若采用TLS估计坐标转换参数,则可较大程度提高参数估计的精度。

