过往策略偏向选择机制对合作的影响研究

盛津芳,沈玉鹏,王 凯,孙泽军

(中南大学 计算机学院，长沙 410083)

1 引 言

演化博弈论为研究自私个体之间的合作行为提供了有力的理论框架[1,2],目前在生物学、经济学和计算机科学等诸多学科里有着非常广泛的应用[3-7].在经典博弈论中,参与博弈的个体是完全理性的,个体为了最大化自身利益选择相应的策略.演化博弈论将经典博弈论与生物学中的演化思想相结合,博弈个体是非完全理性的,在多次博弈过程中,通过不断的学习,来选择最适合自身的策略.常见的博弈模型有囚徒困境博弈[8,9],雪堆博弈[10]和公共物品博弈[11]等.其中,囚徒困境模型得到了最广泛的应用,成为了研究合作演化的经典模型.

在囚徒困境模型中,对于参与博弈的个体而言,通常背叛是一个比较好的策略,因为不用为其他个体提供收益,并且选择背叛可以从合作者那里获得更高的收益.但是合作行为仍然会出现.因此,许多机制被提了出来,用来解释合作产生和维持的原因,比如直接和间接互惠[12-14],迁移[15],惩罚和奖励[16,17]等等.同时复杂网络也为描述合作演化上的拓扑结构提供了非常方便的框架,比如方格网络[18,19],随机网络,无标度网络[20]和小世界网络[21]等等.在图论中,节点表示参与博弈的个体,节点之间的连边表示个体之间存在联系,每个节点可以与相连的邻居发生博弈.参与博弈的个体可能会有不同的特点,而合作水平受到很多因素的影响.例如以前的研究表明有些个体的某些特点将会对合作水平产生很重大的影响,如名誉[22]、年龄结构[23]、学习能力等等[24].

在大多数以前的研究中,都认为参与博弈的个体没有记忆能力.个体在更新自己的策略时,仅根据当前的情况来决定自己的策略,不考虑过往的经验.但在现实社会中,个体都拥有记忆能力,并且在做决策时过往的经验会有很重要的作用.因此,过往的经验对于当前的博弈会存在一定的影响.除此之外,过往研究中个体在选择博弈邻居时往往通过随机的方式来选择本次博弈的邻居,但是在现实社会中个体在进行选择时往往具有某种偏向性.对于一种给定的情况,个体的不同邻居对这个个体的吸引力是不同的,因此个体在选择邻居进行博弈时应该具有某种偏向性.

文献[25]研究了基于记忆的雪堆博弈.在每轮博弈时,每个节点都根据当前相反的策略去获得一个对应的虚拟收益,将虚拟收益与现在的实际收益进行比较,然后将能获得最大收益的策略存入记忆区.每轮迭代结束后,所有节点根据自身记忆区中的过往策略决定选择合作还是背叛,记忆区过往策略集合中合作策略越多,节点选择合作策略的可能性就越高.但是该文献忽视了个体以往的记忆对当前博弈邻居选择的影响.文献[26]研究了基于节点度的偏向选择对囚徒困境博弈合作水平的影响,他们发现节点偏向选择跟自己度差异较小的邻居进行博弈时,合作水平被抑制,而当节点偏向选择跟自己度数差异较大的邻居进行博弈时,合作水平被提高.但该文献仅根据网络拓扑结构来考虑邻居对当前节点的吸引力,未考虑到过往经验对个体的影响.

本文提出了一种基于个体记忆及个体过往策略相似度的偏向选择机制,并研究了该偏向选择机制对合作水平的影响.特别地,提出了记忆区长度M和偏向参数α.在实际生活中,人们的记忆能力是有限制的,记忆区长度M表示了博弈个体对以往策略记忆的能力,M越大表示博弈个体对以往策略的记忆能力越强.同时在实际生活中存在着“物以类聚人以群分”的现象,由于不同的人有不同的决策风格,比较相似的人会更容易相聚成群.但是也存在有些人更愿意去接近那些与自己做事风格不同的人,因此提出了偏向参数α,用来表示个体偏向选择概率与过往策略相似度的相关性.

2 模 型

2.1 预备知识

在经典的囚徒困境模型中,两名博弈对象必须同时决定自己的策略:合作(C)或者背叛(D).如果两个博弈对象同时选择合作,那么两个博弈对象都将获得收益R.如果两个博弈对象同时选择背叛,则两人都将获得收益P.如果一个博弈对象选择合作而另一个博弈对象选择背叛,选择背叛的博弈对象将获得收益T,而选择合作的博弈对象将获得收益S.囚徒困境模型要同时满足T>R>P>S和2R>T+S两个条件才成立.对应的收益矩阵如下:

CD

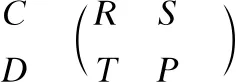
2.2 带偏向选择机制的博弈模型

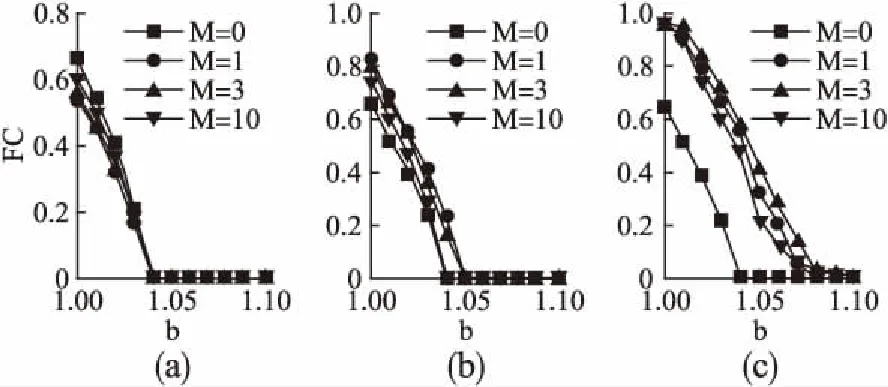
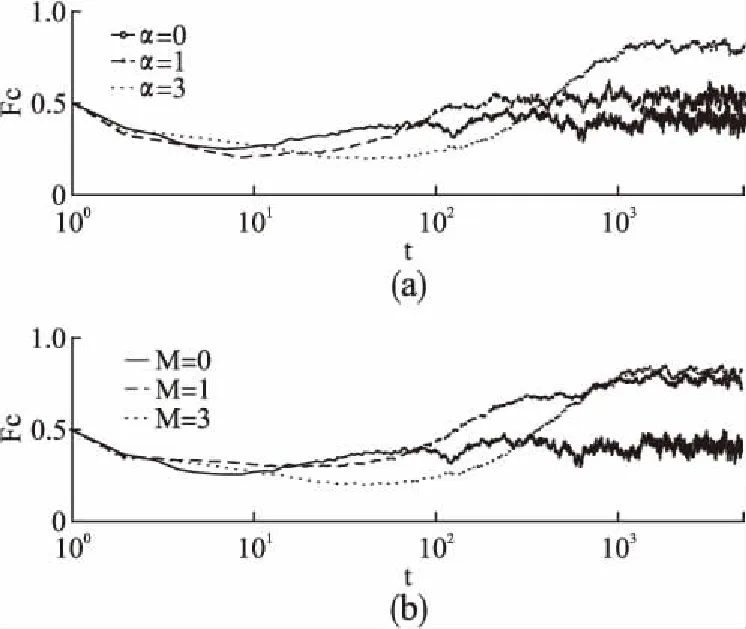
本文使用空间囚徒困境博弈模型,在该模型中,每个个体占据具有周期性边界条件的L×L方格网络中的一个格子.并且本文使用弱囚徒困境博弈模型[27],收益参数设置为R=1,T=b,P=S=0.b的取值范围为1

CD

初始化时,所有节点按照相同的概率被初始化为合作者或背叛者.之后所有节点将按照随机顺序依次更新自己的策略.

在选择博弈邻居时,节点根据偏向选择机制选择邻居节点作为本次的博弈对象,节点i选择自己的邻居j作为博弈对象的概率由公式(1)确定:

(1)

其中,Ω表示节点i的邻居集合.α表示节点偏向选择概率与策略相似度的相关性.由公式(1)可知,当α>0时,节点偏向于选择与自己过往策略相似度较大的邻居,当α进一步增大时,节点对与自己过往策略相似度较大的邻居的偏向性会被进一步增强.当α<0时,节点偏向于选择与自己过往策略相似度差异较大的邻居.当α=0时,节点的所有邻居对其吸引力相同,节点相当于随机选择邻居进行博弈,此时记忆区长度M没有起作用.S(i,j)用来表示节点i与节点j之间的过往策略相似度,S(i,j)定义如公式(2)所示.

(2)

公式(2)中M为记忆区长度,表示博弈个体的记忆能力强弱程度.当M=0时,表示节点没有记忆能力,此时节点之间无法计算相互之间的过往策略相似度,在选择博弈邻居时不具有偏向性,而是随机选择邻居进行博弈.当M>0时,节点拥有记忆能力.初始化时节点记忆区为空,节点第一次博弈时随机选择邻居进行博弈.当进行一次博弈之后,记忆区中开始存在过往策略,随后节点根据偏向选择机制选择博弈邻居.当记忆区中存储的过往策略数量达到所设定的记忆区长度时,之后每次加入新的记忆,都将丢弃距离现在最远的策略记录,以此来保证记忆区长度不超过预先的设定值.在节点i与节点j的记忆区中,如果两节点的过往策略的对应位置相同,则Δn(m)=1,否则Δn(m)=0.如当节点i的记忆区为(C,D,C),节点j的记忆区为(C,D,D),节点k的记忆区为(D,C,D)时,节点i与节点j的过往策略相似度为2,节点i与节点k的过往策略相似度为0.相似度公式表明了节点之间过往策略的相似程度.

在博弈时,节点i将自己的策略替换为邻居j的策略的概率由费米准则[27]确定,费米准则充分考虑了参与博弈的个体不是完全理性的这一特点,同时费米准则体现了一种学习行为.在费米准则中,博弈个体根据双方的收益来决定自己是否学习对方的策略.如果对方的收益比较高,则认为对方的策略是一种比较成功的策略,自己将会有较大的概率学习.费米准则如公式(3)所示.

(3)

在本文中,K的取值为0.1,表示参与博弈的个体具有较小程度的不理性行为.当节点i的收益小于节点j的收益时,节点i有较大的概率将自己的策略替换为节点j的策略,但同时也有较小的概率选择不理性行为,保持自身策略不变.

2.3 演化博弈过程

每轮博弈由以下3部分组成:

1)节点根据偏向选择机制选择邻居;

2)当前更新节点与被选择的邻居分别计算自己的总收益;

3)根据费米准则更新当前节点的策略.演化博弈的具体过程如算法1所示.

算法1.演化博弈的具体过程

步骤1.节点i根据偏向选择邻居j

步骤2.节点i和邻居j计算各自的总收益

步骤3.节点i将当前策略存入记忆区

步骤4.节点i以W(si←sj)的概率同步更新自己的策略

算法1中,步骤1根据公式(1)选择博弈邻居.步骤4根据公式(3)计算节点i更新策略的概率.

3 实验及结果分析

本文使用蒙特卡罗仿真来对演化博弈进行研究,每次实验均由一系列蒙特卡罗时间步组成.网络规模为50×50.并用合作者数量占所有博弈个体数量的比例来表示合作水平Fc.为了获得稳定的结果,每次实验均由5000蒙特卡罗时间步组成,并取最后1000次结果的平均值作为实验结果.

3.1 偏向选择机制对合作水平的影响

图1展示了在不同记忆区长度M和不同偏向参数α下合作水平Fc和背叛诱惑b的关系,将Fc作为b的函数.在图1(a)中,α=-1;在图1(b)中,α=1;在图1(c)中,α=4.每张图中记忆区长度M均有四种取值.当M=0时,表示个体的记忆区长度为0,个体没有记忆能力,此时个体随机选择邻居进行博弈.因此,图1(a)-图1(c)中M=0所对应的合作水平曲线基本相同.

图1 合作水平Fc作为背叛诱惑b的函数Fig.1 Fraction of cooperators Fc as a function of the temptation to defect b

在图1(a)中,当α=-1时,M=0对应的合作水平高于其他的几个M>0对应的合作水平.当M=1时,合作水平达到最低值,之后随着M的增加,合作水平也对应有所增加,逐渐接近M=0所对应的合作水平,但始终低于M=0所对应的合作水平.可以看出,在选择博弈对象时,偏向选择跟图1 合作水平Fc作为背叛诱惑b的函数自己过往策略差异较大的邻居会降低合作水平.虽然随着记忆区长度的增加,合作水平会有所提高,但是无论记忆区长度如何,合作始终受到抑制.在图1(b)中,M=0所对应的合作水平为最低,M=1所对应的合作水平为最高.当M进一步增大时,如3和10,合作水平开始略微降低,但始终高于M=0所对应的合作水平.

在图1(c)中,与图1(b)类似的是当M>0时,合作水平有非常明显的提高.不同的是,M=1所对应的合作水平并不是最高的,当3时,合作水平有进一步的增加,当M=10时,合作水平开始降低,甚至低于M=1时的合作水平,但始终高于M=0时所对应的合作水平.即,随着M的增加,合作水平呈现出先增加后降低的趋势.由此可以得出结论,当个体拥有记忆能力以后,由于偏向选择机制的影响,当个体偏向于选择和自己过往策略更相似的邻居进行博弈时,可以促进合作.同时对比图1(b)和图1(c)可以看出,当α增大时,合作水平也有所增加.并且对于不同的α>0,都存在一个记忆区长度使合作水平达到最大值.

本文根据现实社会的现象来解释为什么个体偏向于选择与自己过往策略比较相似的邻居进行博弈时能促进合作.当博弈双方记忆区的过往策略相似度比较高时,可以认为这两个个体在某些方面有一些相似性,导致他们在同一时刻容易做出相同的策略,那么博弈双方当前策略相同的可能性也比较大.因此偏向选择机制在一定程度上能增加合作者和合作者相遇的概率,降低合作者和背叛者相遇的概率.当合作者和合作者相遇时,双方都不会转变为背叛者,仍然能互相提供收益.但是即使背叛者和背叛者相遇,背叛者也不能从背叛者那里获得任何收益,因此基于过往策略相似度的偏向选择机制在一定程度上有利于合作者的存活.

图2 不同背叛诱惑下的策略分布Fig.2 Strategy distribution under different temptation

为了验证之前的想法,图2中展示了基于随机选择和基于偏向选择博弈邻居两种机制下博弈双方的策略分布.由当前博弈个体与博弈邻居双方的策略组成策略对,共有四种策略对,为别为CC,CD,DC,DD(比如,CC表示本次更新节点和选择的博弈居的策略都为合作).在一次仿真后,将会产生许多策略对,图中展示了在不同背叛诱惑b下,每一种策略对数量占所有策略对数量的比例情况.

从图2(a)和图2(b)中可以看出,相对于随机选择,当个体偏向于选择与自己过往策略更加相似的邻居进行博弈时,合作者与合作者相遇的频率明显增高,而背叛者和背叛者相遇的频率明显下降.可见该偏向选择机制在很大程度上增大了合作者和合作者相遇的概率,由于合作者和合作者相遇不会产生背叛者,因此偏向选择与自己过往策略更加相似的邻居进行博弈时有利于保证合作者的存活,从而提高合作水平.

从图2(c)和图2(d)中可以看出,在偏向选择机制的作用下,合作者和背叛者相遇的频率总体情况下明显降低.但是在某些区间里,如b∈(1.04,1.07)时,基于偏向选择机制进行博弈时合作者和背叛者相遇的频率反而略微高于基于随机选择策略下合作者和背叛者相遇的频率.这是由于在演化博弈初始阶段,合作水平处于下降的趋势,因为此时合作者和背叛者以同等概率初始化,合作者均匀分布在方格网络中,相互之间无法提供收益,这并不利于合作者存活.所以演化博弈初始阶段有很多合作者会转变为背叛者.之后随着迭代次数的增加,合作者形成小的合作者社区,相互之间能提供收益,合作者社区开始向外扩张,直到达到稳定状态.

在b>1.07时,由于背叛诱惑b较大,很快所有节点都成为了背叛者,因此合作者和背叛者相遇的次数较少.而在b∈(1.04,1.07)时,考虑个体记忆区为空时的情况,由于个体之间无法比较过往策略,因此当前博弈个体随机选择邻居进行博弈,此时将会有一部分个体转变为背叛者,这些转变为背叛者的个体记忆区中的过往策略为合作,这反而在一定程度上增加了之后迭代中合作者和背叛者相遇的概率.而在合作者之间形成小的合作者社区之后,合作者社区开始向外扩张,有些背叛者以一种较小的概率遇到合作者,此时合作者由于相互之间能提供收益,所以合作者的收益将远大于背叛者,背叛者将会以一种较高的概率转变为合作者.但是这些由背叛者转变的合作者的过往策略会与背叛者更加类似,此时又进一步增大了合作者和背叛者相遇的概率.

总体来说,偏向选择过往策略更相似的博弈邻居可以增加合作者和合作者相遇的概率,合作者和合作者相遇不会产生背叛者,同时偏向选择机制降低合作者和背叛者相遇的概率,这在一定程度上保证了合作者的存活,由此可以提高合作水平.同时还可以看出,基于记忆及过往策略相似度的偏向选择机制对演化博弈过程产生了影响.

3.2 负相关性偏向选择对合作的影响

为了更加深入的研究负相关性的偏向选择对合作的影响,图3展示了使部分节点按负相关性偏向选择邻居时,合作水平Fc与背叛诱惑b的关系,将Fc作为b的函数,节点在偏向选择邻居时,记忆区长度M有若干固定取值.使合作者偏向于选择过往策略差异更大的邻居,背叛者随机选择邻居,结果如图3(a)所示.使背叛者偏向于选择过往策略差异更大的邻居,合作者随机选择邻居,结果如图3(b)所示.当博弈节点按公式(1)以负相关性偏向选择邻居时,偏向参数α的取值均为-1.

在图3(a)和图3(b)中,M=0表示个体没有记忆能力,该曲线为所有节点随机选择邻居进行博弈时,合作水平Fc和背叛诱惑b之间的关系.

在图3(a)中,M=0所对应的合作水平曲线最高,M=1所对应的合作水平曲线最低,当M增大时,如图M=3和M=10所对应的合作水平曲线,合作水平有略微的增加,但总体来说,合作受到抑制.

图3 负相关性偏向选择对合作的影响Fig.3 Influence of negative preferential selection on cooperation

在图3(b)中,M=0所对应的合作水平曲线最低,M=1所对应的合作水平曲线最高,合作受到较大的促进作用,当M进一步增大时,如图M=3和M=10所对应的合作水平曲线,合作受到的促进作用有略微的减小,但合作仍然受到了促进,合作水平有所提升.

综合上述讨论,可以看出,当节点偏向选择过往策略差异更大的邻居进行博弈时,并不一定会抑制合作.如果仅让背叛者偏向于选择过往策略差异较大的邻居进行博弈,对合作有一定的促进作用.

3.3 偏向选择机制对演化博弈过程的影响

之前已经知道偏向选择机制对博弈演化过程产生了影响,为了更加清晰地展现博弈的演化过程,图4展示了演化博弈在不同迭代次数时,合作水平的快照.其中,b=1.02,黑色表示合作者,白色表示背叛者.初始化时合作者和背叛者被均匀地分散到方格网络中,即每个节点有同等的概率成为合作者或者背叛者.图4(a)-图4(e)是基于随机选择机制的演化博弈在分别经历了0、10、50、500、5000次迭代后的合作水平快照,图4(f)-4(j)是基于偏向选择机制的演化博弈在分别经历了0、10、50、500、5000次迭代后的合作水平快照.

图4 演化博弈过程快照Fig.4 Snapshot during the evolutionary game process

观察从图4(a)-图4(e)以及从图4(f)-图4(j)整个博弈过程中合作者的分布以及数量情况,可以看出,无论是随机选择博弈邻居,还是偏向选择博弈邻居,合作水平都呈现出相同的趋势,即合作水平首先降低,然后又增加,同时合作者从初始时的分散状态慢慢聚集到了一起.这是由于初始化时合作者被均匀分散开,合作者之间不能互相提供收益,由于收益较低,合作者更倾向于学习拥有高收益的背叛者的策略.随着迭代次数的增加,合作者逐渐变少,但是有些合作者已经形成了合作者社区,这些合作者之间可以互相提供收益,由于合作者相互提供相助而获得的高收益,使其不仅能抵御外部背叛者的入侵,还使得背叛者开始学习拥有高收益的合作者的策略.因此合作者社区开始向外扩张,合作水平开始提升.

不同的是,对比图4(b)和图4(c),图4(c)中黑色区域开始扩大,可见在随机选择机制下的演化博弈在t=10时合作水平达到最低,在t=50时合作者社区已经开始向外扩张,合作水平有所提高.而对比图4(g)和图4(h),图4(h)中黑色区域有进一步的缩小,但是黑色区域变的更加集中,在图4(i)中黑色区域才开始扩张.也就是说,在偏向选择机制下的演化博弈在t=50时合作水平才达到最低.这对应之前所说的在演化博弈初始阶段,由于合作者还没有形成小的合作者社区,有些合作者容易转变为背叛者,但其记忆区中的过往策略与其他的合作者比较相似,此时偏向选择机制反而增加了合作者和背叛者相遇的概率,由此造成演化博弈初始阶段合作者社区形成的更慢.可以得出结论,基于记忆区和过往策略相似度的偏向选择机制会对演化博弈过程造成影响,使得合作者之间需要更长的时间来形成合作者社区.同时可以看出,由于偏向选择机制的作用,合作水平有明显的提升.

3.4 记忆区长度M对合作水平的影响

图5展示了当偏向参数α的取值一定时,记忆区长度M对合作水平Fc的影响,将Fc作为M的函数.两个图中α均有若干个取值.图5(a)中,b=1.01,图5(b)中,b=1.02.

图5 合作水平Fc作为记忆区长度M的函数Fig.5 Fc as a function of M

当α=0时,个体的所有邻居被选择的概率相同,此时的偏向选择等同于随机选择,不同的记忆区长度并没有对合作水平造成影响,因此在两图中α=0所对应的合作水平不随着M的变化而变化,几乎为一条水平的直线.而对于不同的α,当M=0时,个体没有记忆能力,此时个体也通过随机的方式选择邻居进行博弈,因此两图中,当M=0时,不同的α所对应的曲线交于一点.

当α<0时,合作水平在M=0时达到最高,此时节点随机选择邻居进行博弈.而当M=1时,合作水平达到最低,之后随着M的增加,合作水平缓慢提高,但始终低于M=0时对应的合作水平.

当α>0时,随着M的增加,合作水平呈现出先增加后降低的趋势,存在一个M使得合作水平达到最高值.同时可以看出,对于不同的α,合作水平达到峰值时所对应的M取值是不同的.如图5(b)中,当α=0时,Fc在M=1处达到最大值,当α=4时,Fc在M=4处达到最大值,当α的取值在合适的范围内增大时,合作水平达到最大值所对应的M也会相应增大.

但是当α继续增大,如图5(a)和图5(b)中,α=5所对应的曲线反而比α=4所对应的曲线要低,合作水平有所降低.当α大于一定值时,可以认为此时节点的偏向选择不是以更高的概率选择过往策略更相似的邻居,而是直接选择过往策略最相似的邻居.因此,考虑个体直接选择与自己过往策略最相似的邻居时的情况,结果如图5(a)和图5(b)中α=+∞所对应的曲线,该曲线处于所有曲线的下方.可以看出,博弈个体直接选择与自己过往策略最相似的邻居并不利于提升合作.因此得出结论,在偏向选择与自己过往策略更相似的前提下,以较小的概率选择其他邻居可以提高合作水平.

3.5 偏向参数α对合作水平的影响

从图5可以看出合作水平Fc并不随着α线性增大,为了进一步查看偏向参数α对合作水平Fc的影响,图6展示了当记忆区长度M的取值一定时,偏向参数α对合作水平Fc的影响,将Fc作为α的函数.两个图中M均有若干个取值.图6(a)中,b=1.01,图6(b)中,b=1.02.

图6 合作水平Fc作为偏向参数α的函数Fig.6 Fc as a function of α

当α=0时,节点随机选择邻居进行博弈,因此两图中,不同的曲线在α=0处交于同一点.当M=0时,个体随机选择邻居进行博弈,α没有起作用,因此两图中M=0所对应的合作水平不随着α的变化而变化,几乎为一条水平的直线.而当M>0时,α对合作水平产生了影响.当α<0时,M>0所对应的曲线均处于水平线的下方,合作被抑制.而当α>0时,合作水平首先升高又降低.当α的取值在合适的范围时,如两图中α∈(0.6)时,M>0所对应的曲线均处于水平线的上方,该偏向选择机制可以促进合作.但当α超过一定的范围时,如两图中,M=1,α=7时,合作反而受到抑制.这对应之前所获得的结论,并不是选择过往策略相似度最高的邻居可以促进合作,而是以一种比较高的概率选择过往策略比较相似的邻居时,可以促进合作.同时可以看出,对于不同的M>0,合作水平Fc均在α=4时达到最大值.

3.6 偏向参数α和记忆区长度M对演化博弈过程的影响

之前已经得出结论,偏向选择机制对演化博弈过程产生了影响.本文进一步研究了M和α对演化博弈过程的影响,图7展示了在不同的记忆区长度M和偏向参数α下合作水平Fc随着迭代次数t的增加而变化的时序图.图7(a)中,b=1.02,M=3;图7(b)中,b=1.02,α=3.在演化博弈过程中,在合作水平达到最小值时,合作者社区已经形成,随后合作者社区开始向外扩张,合作水平开始提升.使用Fcmin来表示演化博弈期间合作水平Fc所能达到的最小值.

从图7(a)可以看出α=1和α=3的Fcmin来对应的t大于α=0的Fcmin对应的t,图7(b)中M也呈现出了和α相同的规律,M=1和M=3的Fcmin对应的t大于M=0的Fcmin对应的t.当M=0时,节点没有记忆能力,节点随机选择邻居进行博弈;当α=0时,节点的不同邻居对节点的吸引力相同,节点也通过随机的方式选择邻居进行博弈.可以得出结论,在演化博弈过程中,节点偏向于选择与自己过往策略更相似的邻居会使合作者社区形成得更慢.

不同的是,在图7(a)中,当α从0增加到3时,Fcmin对应的t也显著增加,且α=1和α=3所对应的Fcmin的值几乎相等.在图7(b)中,M=1和M=3时Fcmin对应的t相差很小,且M=1和M=3所对应的Fcmin的值相差很大.也就是说,偏向参数α对合作者社区形成所需要的时间有较大的影响,但最终合作者社区形成时,偏向参数α并不影响当时的合作水平.而记忆区长度M与偏向参数α相反,记忆区长度M对合作者社区形成所需要的时间影响较小,但最终合作者社区形成时,记忆区长度M对当时的合作水平有较大影响.

图7 α和M对演化博弈过程的影响Fig.7 Influence of α and M on the evolutionary game process

此外,从图7(a)和图7(b)中可以看出,在演化博弈达到稳态时,更大的α或更大的M对应着更大的t,也对应着更大的Fc.并且在图7(a)中,不同的α对应的Fc相差较大;在图7(b)中,不同的M对应的Fc相差较小.说明了当记忆区长度M和偏向参数α在适当的区间内增加时,演化博弈达到稳态所需要的时间更长,并且最终所能达到的合作水平更高,而偏向参数α对合作水平的影响要大于记忆区长度M对合作水平的影响.

4 结 论

本文提出了一种新的基于个体记忆以及个体过往策略相似度的偏向选择机制,并且使用了囚徒困境博弈模型,在方格网络上研究了该偏向选择机制对合作的影响.结果显示,当偏向参数α>0且取值在合适的范围内,即个体偏向选择过往策略更相似的邻居进行博弈时,合作水平有非常明显的提高,而当偏向参数α<0时,即个体偏向选择过往策略差异较大的邻居进行博弈时,合作受到抑制.对于给定的α,存在M使合作水平达到最大值.同时,该偏向选择机制会增加演化博弈达到稳态所需要的时间.并且α和M对演化博弈过程也有不同的影响.当M一定,α变化时,合作者社区形成得更慢,但并不影响合作者社区形成时的合作水平.而当α一定,M变化时,合作者社区形成所需要的时间相差不多,但当合作者社区形成时,合作水平会有很大的差别.