一种融合多因素社交活动个性化推荐模型
陈 艺
(四川文理学院信息查询与利用教研室 四川 达州 635000)
Probabilistic matrix decomposition
0 引 言
随着互联网技术的飞速发展,社交媒体和电子商务等迅速发展,互联网数据呈指数级增长。人们不仅是数据的制造者也是数据的消费者,如何从庞大的数据中筛选用户感兴趣的信息成为学者们亟需解决的问题。对于用户而言,感兴趣信息的获取可通过搜索获得,也可借助推荐算法推荐得到。与搜索引擎相比,推荐算法不需要用户主动提供所需信息,而是根据少量信息构建用户兴趣模型,进而利用数据挖掘获得数据背后的信息。2006年DVD在线租赁商Netflix通过悬赏奖金的形式鼓励学者们完善个性化推荐算法,期间大量针对传统协同过滤推荐的改进算法被提出来。而协同过滤推荐过度依赖于“用户-项目”评分数据,将其引入到社交兴趣推荐中后难以获得满意的推荐效果。
针对社交大数据的特殊性,研究学者们提出了不同的解决方案。文献[1]基于位置的社交网络中用户历史兴趣点,利用变阶马尔科夫算法来预测用户未来到达的兴趣点,算法提高了兴趣点的推荐效果;文献[2]将用户物品图引入信任机制建立用户信任图,在信任社交网络中提出了一种基于图熵的个性化推荐算法,不仅有效缓解了推荐的冷启动问题还保持较高的推荐准确率;文献[3]挖掘项目间的全局项目相似信息,并将社交网络用户间的可靠度融入个性化推荐模型中,提出了一种改进的社交网络个性化推荐算法,降低了冷启动问题;文献[4]引入时间函数推断用户的兴趣向量,并利用聚类算法对用户发布的微博内容进行聚类分组,以用户兴趣向量筛选最佳匹配,并进行排序,取得了较好的推荐结果;文献[5]对社会网络推荐研究进行了系统述评,提出了一种融合项目特征和移动用户信任关系;文献[6]将用户间的信任关系引入个性推荐模型中,以解决数据稀疏问题;文献[7]通过优化基于内容的CF推荐模型,有效解决了个性推荐中的冷启动问题;文献[8]提出了一种结合社交关系和位置信息的地点推荐算法,缓解了数据稀疏和冷启动问题;文献[9]提出了基于多元社交信任的协同过滤推荐算法,利用用户间的综合信任关系选取推荐邻居,算法有较高的推荐精度和较强的抗攻击能力;文献[10]提出了一种具有社交影响力的推荐算法,通过用户的影响力不断调解推荐的权重;文献[11]提出了基于项目评分与用户信任关系的CF推荐算法,通过评分用户间的信任关系来挖掘用户的社会关系与兴趣偏好;文献[12-14]利用位置信息来对用户进行分类,借助其他属性对类内用户进行信任预测或计算,从而完成个性化推荐。以上文献研究中,文献[2-3,6-7,9,11]都是在协同过滤的基础上融合其他属性来提高分类的精度;文献[1,4-5,8,10]主要是在融合用户兴趣度、活动地理位置等影响因素的基础上获得较高的推荐效率。
针对社交平台日益庞大的数据以及用户个性的多样化,学者们提出或改进的社交网络个性化推荐算法,一定程度上提高了因数据稀疏性导致的推荐精度问题,但单一社交活动属性的个性化推荐算法难以有效获得高精度推荐结果。为此本文综合用户对活动兴趣度、活动召集者影响力以及活动举办地点偏好等三方面因素形成一种新的个性化推荐模型。
1 模型描述
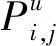
(1)

1.1 构建用户对活动兴趣度的概率模型
用户对社交活动内容的兴趣度是影响用户是否参加活动的重要因素。本文利用LDA(Latent Dirichlet Allocation)文件主题模型求取用户ui与其参加过的所有社交活动的主题分布,并用用户ui的主题分布表征其兴趣度。在LDA中,设ψs表示隐含主题s在单词集合上的多项式分布,docui表示用户ui∈U所有参加过的社交活动内容形成的文件,对于docui可经过LDA文件主题模型求取其中所有隐含主题的多项式分布,而用户对社交活动的兴趣度可以表示成文件docui的主题概率分布。若对某社交活动内容的文件docui中含有Nk个隐含主题,则LDA对隐含主题的多项式分布求取过程:
Step1利用LDA分布函数Dirichlet(δ)对文件docui中的每个隐含主题s∈{1,2,…,Nk}生成隐含主题与单词的概率分布ρs;
Step2利用LDA分布函数Dirichlet(γ)对文件docui中的每个文件生成文件与单词的概率分布τdocui;
Step3利用LDA多项式分布函数Mult(τdocui)对文件docui中的第m单词生成主题分配sdocui,m;
Step4利用LDA多项式分布函数Mult(ρsdocui,m)对文件docui中的第m单词生成wdocui,m。
用户文件docui的似然函数为:
f(sdocui,m|ηdocui)·f(ηdocui|γ)·f(Γ|δ)
(2)
式中:δ、γ为LDA分布函数的参数,wdocui、Mdocui、ηdocui、Γ分别表示文件docui中所有单词、单词的数量、单词的主题分配、单词对应的主题-单词概率分布。
设在LDA文件主题模型中文档间是相互独立的,则M个文件的完全似然函数如下:
(3)
式中:W、S、Φ分别表示文件中所有单词、主题的分布以及所有文件-主题词概率分布。我们几乎不可能从似然函数中推断出参数Φ和Γ,并且难以直接从某一多变量概率分布中近似抽取样本序列,因此,本文采用吉布斯采样将隐含主题词s从联合的概率分布中采样出来:
f(si=k|s-i,wi=z,w-i)∝
(4)
(5)
(6)
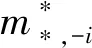
(7)
设用户ui的文件为docui,社交活动aj的文件为docaj,两者所对应的主题分布为τdocui和τdocaj,为了求取用户与社交社交活动的主题的相似度,本文引入库尔贝克-莱布勒散度(Kullback-Leibler,KL)[15]和延森-香农散度(Jensen-Shannon)[16]来计算两者之间的相似度。延森-香农散度定义为:
(8)
式中:KL(·)表示库尔贝克-莱布勒散度。其定义为:
(9)
JS(ui‖aj)会随着τdocui和τdocaj两者主题分布的差别而增大,这里定义用户ui对社交活动aj的兴趣度Ii,j为:
Ii,j=1-JS(ui‖aj)
(10)
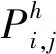
(11)
1.2 构建用户对召集者影响力概率模型
在基于活动的社交网络中,用户是否参加某项活动也跟活动召集者的影响力有关,或者说一大部分用户是慕名参加社交活动。本文认为用户参与某项社交活动受两方面的影响:一是用户对活动召集者的偏爱或慕名;二是用户对社交活动本身的兴趣或偏爱。这两方面的影响很难直接获得,本文将用户参加某个召集者或某类社交活动的次数来量化影响力。设用户ui参加某活动召集者ci组织的社交活动次数为cui,j,cui,j值越大说明召集者ci组织的活动对用户ui的影响力越大。这里我们将构建一个用户与召集者间的影响力矩阵C,通过基于影响力的概率矩阵分解来对矩阵进行精确的分析,力求得到用户基于召集者影响力参与社交活动的概率。
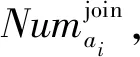
(12)
式中:λ(0≤λ≤1)为权重因子,EA表示所有结束的社交活动集合。将召集者ci所有曾经组织的社交活动平均影响力来表示召集者ci的影响力:
(13)
式中:ENci表示召集者ci曾经组织的社交活动集合。
影响力矩阵C条件分布如下:
Efcj),σ2)]Vi,j
(14)
式中:Ν(x|μ,σ2)表示均值μ方差σ2的高斯分布,当用户ui参加召集者ci组织的任何一场活动时Vi,j=1,否则为0。D、Q、Numu、Numc分别表示所有用户和所有召集者的隐式特征矩阵以及用户数量和召集者数量。针对用户和召集者的隐式特征矩阵,这里利用均值μ=0的高斯先验分布去求解:
(15)
(16)
对上进行取对数,后验分布可得:
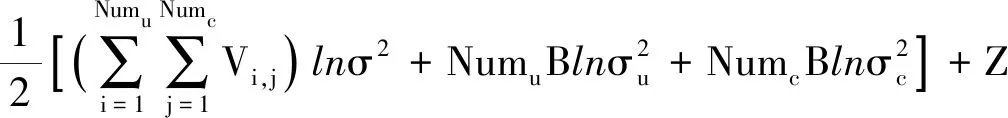
(17)
式中:B表示隐式特征矩阵维度,Z为常量。将上式最大化可得一个等价目标函数,该函数由二次正则化项平方误差和范数平方组成:
(18)
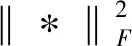
(19)
经过模型的学习可以得到所有用户和所有召集者的隐式特征矩阵D、Q,那么对于用户与召集者间的影响力矩阵C中的缺失值可由下式进行估值:
(20)
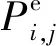
(21)
1.3 构建用户因地理位置偏好的概率模型
基于活动的社交网络具有线上交流线下活动的特点,所以活动举办地也是影响用户是否参加活动的重要因素之一。针对地理位置偏好对用户参加社交活动的影响度,学者们进行了大量的研究,得出的结论也大体一致:用户参加的大多数活动与之常住位置距离不远,并且该距离分布函数近似幂律分布[17-18]。本文基于活动举办地与用户常住距离,以用户参加活动的频数来对用户地理位置偏好建模。在学者研究成果的基础上,将活动举办地与用户常住距离的概率定义为:
p(Dis)=ν·Disζ
(22)
式中:Dis表示活动举办地与用户常住地之间的距离,ν、ζ为幂律分布函数的参数。对式(22)取对数来估算参数ν、ζ的值:
logp(Dis)=logν+ζlog(Dis)
(23)
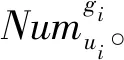
(24)
式中:Dis(gi,gaj)表示地理位置gi、gaj间的距离,那么用户ui基于地理位置参加社交活动aj的概率为:
(25)
2 实验数据与参数设置
2.1 实验数据及评价标准
为了获得较大的数据量,本文选取一线城市北京和上海作为社交活动举办地,社交数据采集豆瓣同城在2017年1月1日-2018年12月31日期间举办的所有社交活动,主要采集的信息为:用户信息(用户名、用户ID、用户的兴趣、用户参加过的所有社交活动、用户所在的位置等),社交活动信息(社交活动类别、社交活动的内容,社交活动召集者、社交活动举办地、社交活动ID等)。数据统计如表1所示。

表1 数据统计明细
仿真实验将Top-N推荐算法推荐结果,采用Precision@N和Recall@N两个评价指标评估各算法推荐的性能:
(26)
(27)
式中:U表示用户集合,Reui,N、Tui分别表示利用各算法按照Top-N推荐给用户ui的社交活动以及用户ui在测试集中所参与的活动集合,|*|为计算集合大小,这里设置N=1,3,5,7,10,本文默认N=5。
2.2 参数设置
在LDA文件主题模型、召集者影响力概率矩阵分解模型中需要对参数进行优化设置。各模块参数设置如下:
(1) LDA文件主题模型参数设置。实验采用自然语言处理框架Gensim实现LDA文件主题模型,在模型中设LDA分布函数参数γ=50/Nk,δ=0.01,为了获得隐含主题s的最佳个数Nk,利用豆瓣同城北京和上海数据集测试LDA在不同的Nk下Precision@5和Recall@5,结果如图1所示。
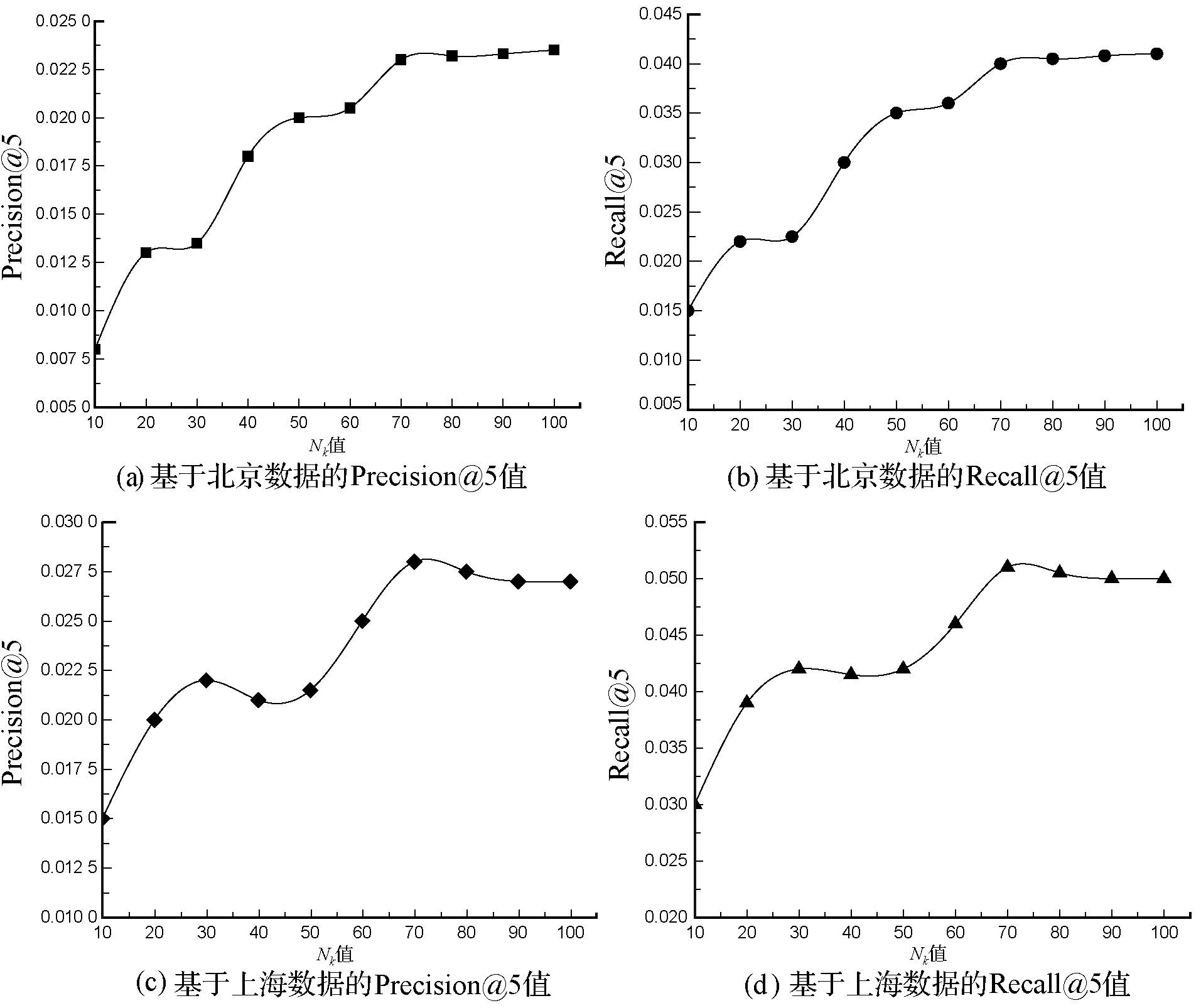
图1 不同隐含主题个数下Top-5结果
可以看出:在豆瓣同城北京数据集上,Precision@5和Recall@5随着隐含主题个数的增大而增大,在Nk≤70阶段,推荐准确度增加幅度较大,在70 图2 不同隐式特征矩阵维度下Top-5结果 可以看出,在基于影响力的概率矩阵分解模型中,随着隐式特征矩阵维度B值的增大,Top-5推荐评价指标Precision@5和Recall@5波动变化。在豆瓣同城北京数据集上,随着维度B值的增大,推荐评价指标Precision@5和Recall@5值在振荡减小;在豆瓣同城上海数据集上,在10≤B≤80阶段,随着维度B值的增大,推荐评价指标Precision@5和Recall@5值在振荡增大,在80 为验证本文所提算法的性能,将本文算法与文献[8,19]进行社交活动推荐效果对比分析。文献[8]利用兴趣度计算相似用户,借助用户历史地点签到记录获取位置偏好信息,融合两者提出了一种推荐算法;文献[19]利用相似关系、兴趣偏好建立一个社交活动参与模型,利用依靠移动社交媒体,如射频识别(RFID)、蓝牙设备等建立社交活动临近模型,然后将两者融合以推导用户的潜在偏好和潜在的社交关系。硬件环境为Intel(R) Core(TM) i7-7700U@3.6 GHz,RAM:8 GB。软件环境为:Windows 7操作系统,使用Python编程实现。利用网格搜索在豆瓣同城北京和豆瓣同城上海数据集上多次实验得到参数α、β的最优设置。在豆瓣同城北京数据集上β=0.3,α=0.6,在豆瓣同城上海数据集上β=0.35,α=0.45,其他参数按照2.2节进行设置。为了验证本文个性推荐算法的优越性,从两个层面进行对比:一是将本文融合多因素推荐算法与单因素推荐算法进行推荐效果对比;二是将本文算法与同类推荐算法进行推荐效果对比。 本文算法综合用户对活动兴趣度、召集者影响力及地理位置偏好等三方面的因素进行个性化推荐。为了对比综合后的推荐效果,这里将三种单因素推荐算法与本文算法在两个数据集上进行Top-N(N=1,3,5,7,10)推荐评价指标对比。设基于用户对活动兴趣度的推荐算法为UIA,基于召集者影响力的推荐算法为CI,基于地理位置偏好的推荐算法为GLP,推荐效果如图3所示。 图3 各算法Top-N推荐评价指标对比 如图3所示,通过本文算法与其他三种算法在Top-N(N=1,3,5,7,10)下的推荐评价指标对比可以看出,在豆瓣同城北京和上海数据集上,三个单因素个性推荐算法的推荐效果是有差异的。在北京数据集上UIA算法效果优于其他两个单因素推荐算法;而在上海数据集上CI效果优于UIA和GLP两个单因素推荐算法。但总体上看本文算法在综合用户对活动兴趣度、召集者影响力及地理位置偏好等三方面的因素后,推荐效果远远好于三种单因素推荐算法。在准确率上,本文推荐算法相较于三个单因素个性推荐算法至少提高了36.7%;在召回率上,本文推荐算法相较于三个单因素个性推荐算法至少提高了35.9%。 将三种算法对已有用户社交活动的推荐结果进行对比分析,结果如图4所示。 图4 各算法Top-N推荐评价指标对比 可以看出,本文提出的个性化推荐算法在不同N值下的推荐指标明显好于其他两种推荐算法,说明本算法在综合用户兴趣度、召集者影响力和地理位置信息后能够取得较好的推荐结果。图4(a)和图4(b)为各算法在豆瓣同城北京数据集上的推荐结果,在Top-N(N=1,3,5,7,10)的推荐中,本文算法相较于文献[8]和文献[19]的准确率至少提升了11.42%和18.18%,召回率至少提升了约14.71%和23.64%;图4(c)和图4(d)为各算法在豆瓣同城上海数据集上的推荐结果,本文算法相较于文献[8]和文献[19]的准确率至少提升了8.77%和19.23%,召回率至少提升了约8.57%和12.52%。 本文综合用户对活动兴趣度、活动召集者影响力以及活动举办地点偏好等三方面因素,采用不同权值配比综合形成最终的社交活动个性推荐模型。对比实验表明,本模型不论与三个单模块个性推荐模型还是与其他两个同类网络社交活动推荐模型相比准确率和 召回率都有一定的提高。推荐精度的提高可能要增加 时间和空间消耗,将本文模型并行化处理以降低时间 复杂度是后续研究的重点方向。
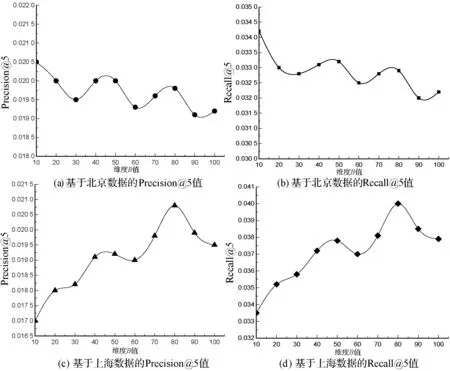
3 仿真实验与对比分析
3.1 推荐效果对比
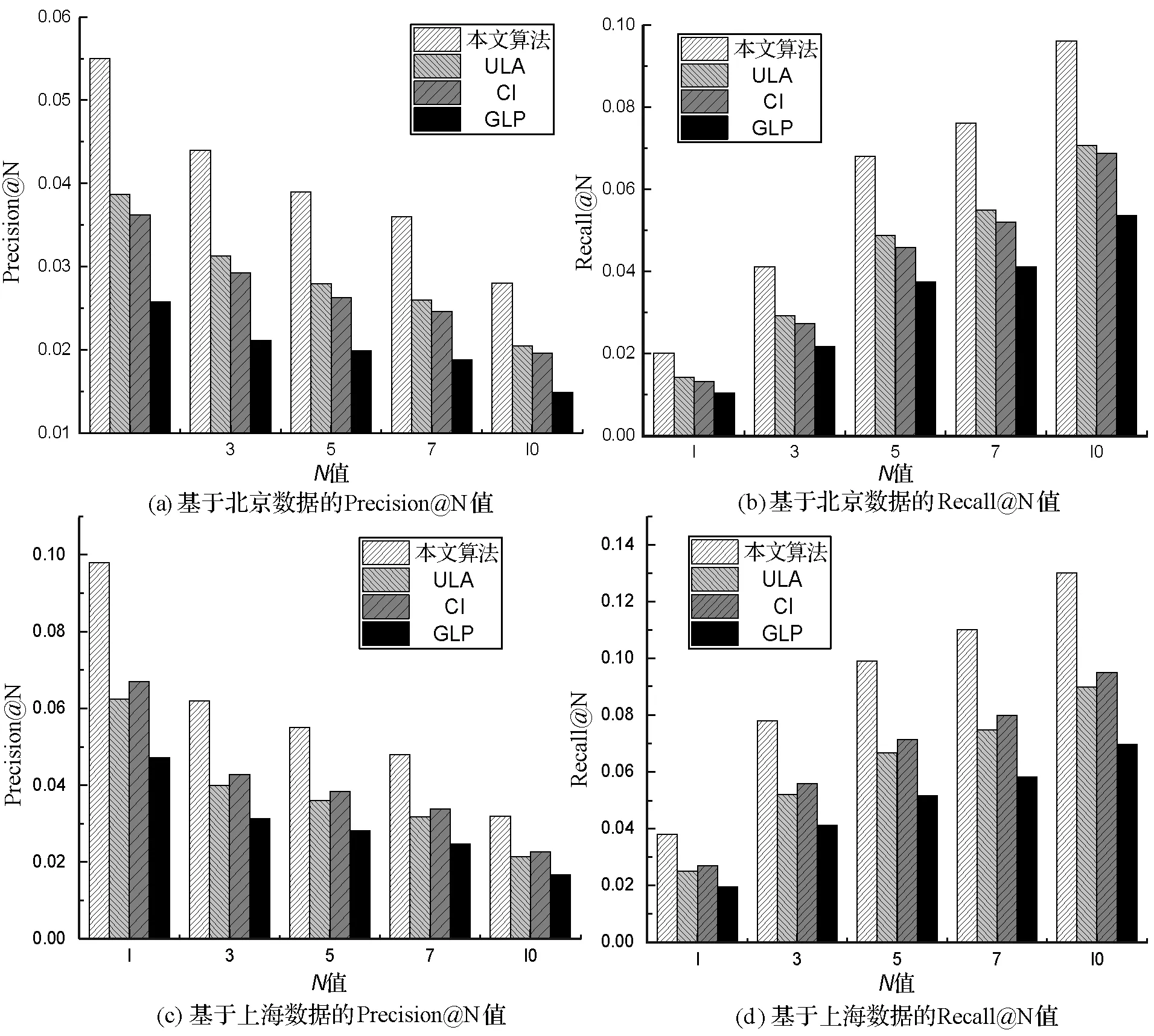
3.2 同类推荐效果对比
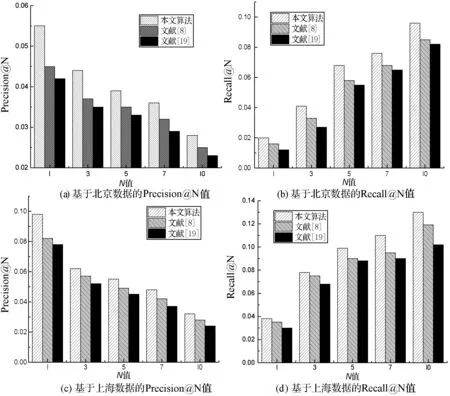
4 结 语

