重装备公路输送对民用大型平板拖车数量需求分析
裘大明, 刘宝新, 徐伟剑
(1.陆军军事交通学院学员五大队研究生队,天津 300161;2.陆军军事交通学院联合投送系,天津 300161)
我军现役重装备运输车价格昂贵、维修保养费用高,平时动用少、战时或紧急情况下需求量大,如果完全按照战时需求比例进行编配,必然造成巨大的军费开支和不必要的资源浪费。随着国民经济快速发展,民用大型平板拖车数量不断增多[1],很多不经改装或稍加改装,即可用于运送履带式重装备,能有效解决部队重装备运输车编配较少的问题[2]。近年来部队重装备实施公路运输投送任务增多,对民用大型平板拖车的需求增大,部队接到任务时,向上级提报的民用大型平板拖车数量需求常常“经验主义”至上,缺乏科学的筹划安排和精确的计算。分析部队实施重装备公路运输投送的任务,对两种类型的任务形式分别确立计算方法,旨在科学合理地分析不同情形下的民用大型平板拖车数量需求,为部队提报需求提供有益参考。
1 重装备公路运输投送任务分类
部队任务不同,其对于重装备运力的需求轻重缓急也有所区别。各部队实施作战任务、实兵演习、年度训练、转场机动等多种形势的重装备公路运输投送任务,从组织方式上来看,重装备公路运输投送任务可以归纳为两类:
(1)部队实施公路远程机动,需要征用民用大型平板拖车。即使用民用大型平板拖车运力完成部队重装备向作战地域快速机动布势,或在战争进行时部分送修、补充履带式装备的运输投送任务,以及部队返营阶段的长距离机动任务。
(2)部队重装备短距离高强度倒运,需要征用民用大型平板拖车。短距离高强度倒运,包含多种倒运方式,如将重装备由驻地倒运至铁路装载站、装载站至码头、机场等多种场合,适用于部队由驻训地直接开进至作战演习地域、演习地域或驻训地直接向战场开进等情况。既无法短时再征用大量民用运力,又没有距离较近的大型装载站可供使用,只能利用重型合成旅当前所拥有的编制、配属和征用民用运力往返数次,协同完成所有履带装备中短距离的高强度倒运。
2 民用大型平板拖车数量需求分析
分析民用大型平板拖车数量需求模型,需要将长距离远程运输投送和短距离高强度倒运两种情形区别开,分别建立长距离运输投送运力需求模型和短距离倒运运力需求模型,对不同任务下部队重装备完成运输投送任务需要征用的民用型平板拖车数量进行定量分析。
2.1 长距离运输投送运力需求分析
部队重装备长距离远程运输投送任务是保障的难点,其要大规模征用民用运力予以保障,并且这样的保障行动一定是混合了编制运力、加强运力,可能还会有战略投送支援车队运力、国防交通专业保障队伍等,以及临时征用的分散运力。
2.1.1 建立需求模型
纵观世界各国军队,在实战条件下,部队重装备整建制长距离运输投送工作中,很难达到所有重装备运力与履带式装备数量比例达到1∶1的情况,美军在伊拉克战争中,通过征用、购买和增配,这一比例勉强达到1∶3。本文建立的长距离运输投送运力需求模型,仅限于“长距离、小规模、仅公路、且急需”的这类特定条件下任务进行假设。
我军现有的编制重装备运输车、上级加强的重装备运输车以及征用的符合条件的民用大型平板拖车数量应当不低于整建制部队重装备数量。同时,考虑在长距离运输投送途中,装备总体存在故障率,且部队重装备预留机动运力,用于应对突发情况出现的需求增加,那么应当存在如下数学关系:
Q=(Y编+Y加+Y民)×(1-λ)÷(1+φ)
(1)

(2)
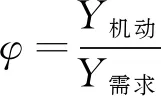
(3)
式中:Y编为部队重装备编制重装备运力;Y加为上级加强重装备运力;Y民为需动员的民用大型平板拖车运力;Yi(故障)为发生故障的重装备运力;Yi(总数)为重装备运力总数;Q为部队重装备数量;λ为重装备运力总体故障率;φ为预留的机动运力比例。
则需要动员的民用大型平板拖车运力需求为:
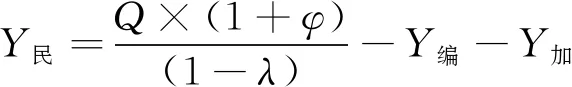
(4)
2.1.2 实例分析
以某部实施长距离远程运输投送机动任务为例,给出模拟数据,对民用大型平板拖车数据进行测算。该部需运输投送履带式装备Q=60台,Y编=12台,Y加=18台,λ=10%,φ=5%,代入式(4)后可得Y民=40台,即需要动员的符合条件民用大型平板车数量为40台。
2.2 短距离倒运运力需求分析
部队重装备短距离高强度倒运,需要在较短的时间内征用的大型平板拖车数量相对较少,并且倒运距离一般都在100 km以内,可以很容易地征用到符合条件或者近似符合条件的民用运力。
2.2.1 建立需求模型
对于部队重装备短距离高强度倒运问题,应当予以简化分析,见图1。从图1可看到可能存在的各点之间的倒运任务,其中:D1表示战场;D2表示驻(训)地;D3表示装(卸)载站;D4表示机场/码头;D5表示演习场;Sij表示Di至Dj距离(i=1,2,3,4,5;j=1,2,3,4,5,i≠j)。
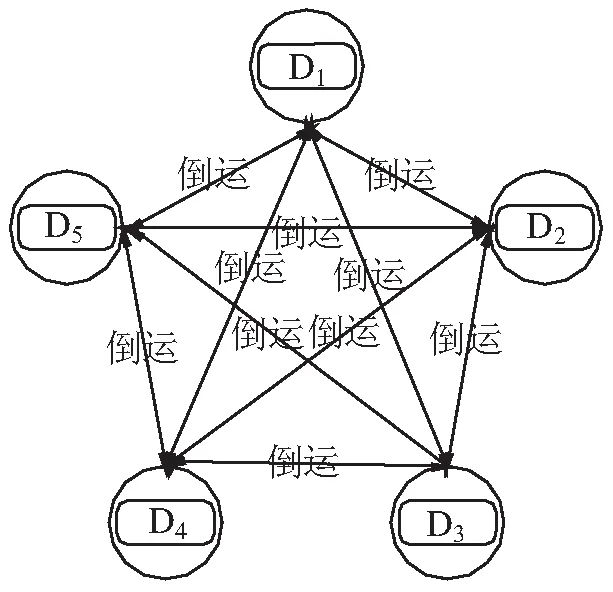
图1 倒运任务图
例如,某重型合成旅接上级命令,X台重装备需由驻地至装载站,经铁路运输方式抵达演习场所在卸载站,再倒运至演习场。即先由D2至D3,再由D3至D5。总结各倒运点之间可能存在的倒运任务,如表1所示。

表1 部队重装备短距离高强度倒运任务
不同任务条件下,所需运输的履带式重装备的总体数量给定,记为Qij。不同路线条件下,由于道路等级不同、路况条件各异,重装备运力在空载和满载情况下的平均时速一定,且可以测得。记:Qij为Di至Dj路线条件下的装备总数;Vij为Di至Dj路线条件下的平均车速;λij为Di至Dj路线条件下重装备运力总体故障率;φij为Di至Dj路线条件下部队重装备预留的机动运力比例。
如图2所示,分析单车装载、运行、卸载、返回、再装载的过程。记:T1为单车运行所需时间;t装为装载履带式装备所需时间;t卸为卸载履带式装备所需时间;t运ij为单车满载出发至卸载点以及空载返回至装载点总时间。
可以得到,单车运行一个来回所需总时间:

图2 单车运行示意图
但在实际工作中,通常装载点、卸载点不止一个,并且车辆在装载点可能存在等待装车、卸载点可能存在等待卸载的情况,如图3所示。记:m为装载点可容纳同时装车的数量;n为卸载点可容纳同时卸车的数量;Yij为不同任务下运力总量;[]表示向上取整,即符号内的数字取其整数部分并+1,如[3.2]=4;{}表示向下取整,即符号内的数字取其整数部分,如{3.2}=3。

图3 实际倒运示意图
(1)当m>n时。即装载点充裕、卸载点紧张,装载点按顺序完全装完所有车辆,但卸载点由于卸载数量少,导致返回的运力较少,装载点有空闲,要使得倒运时间最短,应当以计算卸载点时间为基点。

(6)
需要的最优运力Yij应当满足:

(7)
即第一批返回运力抵达装载站时,第一批所有车辆正好装完。又有:
Yij=(Y编ij+Y加ij+Y民ij)×(1-λij)÷(1+φij)
(8)
根据式(6)、式(7)、式(8),可以得到:
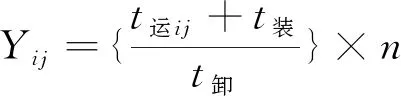
(9)

(10)
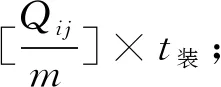
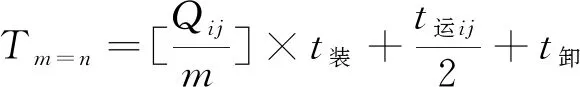
(11)
(3)当m (12) 将式(10)、式(11)合并,即可得到,当m≤n时: (13) 需要的最优运力Yij应当满足第一批返回运力抵达装载站时,第一批所有车辆正好装完,即: (14) 由式(12)、式(13)、式(14)可以得到如下数量关系: (15) (16) 即在任意任务需求情况下,获得必要已知条件,部队重装备可通过上述数量关系,求出最优解[4]。 2.2.2 实例分析 以某部队重装备实施短距离倒运任务为例,给出模拟数据,对民用大型平板拖车数据进行测算。 某部200台重装备需由驻地向演习场开进,通过短途倒运的方式开向驻地最近的铁路装载站。已知该部队驻地距离装载站为55 km,重型平板拖车以往测得的平均车速为60 km/h,该旅平时训练中获得的履带式装备单车装载时间为15 min,卸载时间为10 min;驻地开设的装载场可同时组织大规模装载的站台有6个,铁路装载站可供大量同时卸载站台4个;该旅现有编制内完好的重装备运输车10台,上级为保障该旅本次任务,加强了6台重装备运输车;该旅战区范围内重装备运力故障率λij=10% ,该旅预留的机动运力比例φij=8%,求该旅以高强度短途倒运完成此次任务耗时,并需要征用多少辆符合条件的民用大型平板拖车。 代入式(6),得到:Tm>n= 570 min。 代入式(9),得到:Yij=50台。 代入式(10),得到:Y民ij=44。 综上,该部队以高强度短距离倒运完成此次任务需要用时9时30分,需要征用符合条件的民用大型平板拖车数量为44辆。 部队实施公路重装备运输投送任务时,可以根据情况判断属于长距离远程运输投送和短距离高强度倒运哪种情形,分别科学测算出不同变量的具体数值,根据部队实际情况,确定需要征用的民用大型平板拖车数量。
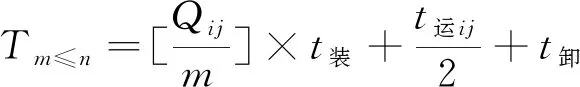

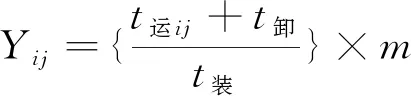

3 结束语

