基于PCA与t-SNE特征降维的城市植被SVM识别方法

于慧伶, 霍镜宇, 张怡卓, 蒋 毅

(1.东北林业大学 a.信息与计算机工程学院； b.机电工程学院，哈尔滨 150040； 2.黑龙江省计算中心，哈尔滨 150001)

0 引 言

城市植被是城市平衡、协调发展的重要组成部分，对构建生态城市起着举足轻重的作用。近年来，随着高光谱技术的发展，高光谱技术已经广泛地应用于城市植被的精确获取和动态监测[1]。高光谱图像具有数据量大、数据维数高和数据冗余性强等特点[2]。如果直接对获取的用于城市植被提取的高光谱图像数据进行分类，庞大的数据量不仅会影响运行的速度，也会降低分类器的泛化能力，影响分类的精度，从而无法得到理想的分类结果[3]。高光谱图像分类常常需要先进行数据降维等预处理操作[4]。

目前，高光谱图像降维主要分为线性降维和非线性降维两类。线性降维主要包括主成分分析法(Principal Component Analysis，PCA)和线性判别式分析(Linear Discriminant Analysis，LDA)及相应的改进算法等[5]。非线性降维主要包括局部线性嵌入算法(Locally Linear Embedding，LLE)和等距离映射算法(Isometric Mapping，Isomap)及相应的改进算法等[6]。白杨等[7]提出了一种改进的K2DPCA方法，但这种方法需要较多的主成分来重新构建原始的高光谱图像，降维效果并不理想。张鹏强等[8]提出了基于核半监督判别分析的方法，在训练样本较少的情况下可以将特征空间中的样本数据更好地聚类，但是在训练样本较多的情况下，该算法的分类精度不是很高。杨磊等[9]利用基于流形学习的非线性降维算法对高光谱图像进行特征提取，实验结果表明，Isomap算法降维时间较长，LLE和拉普拉斯特征映射算法(Laplacian Eigenmaps，LE)需要更多的特征波段才能得到较好的分类效果。吴东洋等[10]对于高光谱图像降维和分类提出了多流形LE算法，但在度量同一类之间的权值时不准确。

流形学习中的t-分布式随机邻域嵌入算法(t-Distributed Stochastic Neighbor Embedding，t-SNE)是可以用来可视化数据降维的一种方法[11]。该算法不仅能将流型上的附近点映射到低维表示中的附近点，还能保留所有尺度的几何形状，即将附近的点映射到附近的点，将远处的点映射到远处的点，但是该算法内存占用大，运行时间较长。如果在保持基本上不丢失信息的前提下，先利用PCA算法对高光谱图像进行初步的降维，然后再利用t-SNE算法进行二次降维处理，可以提高运算效率。本文将PCA与t-SNE降维方法融合用于城市植被信息提取的高光谱图像降维，然后利用支持向量机(Support Vector Machine，SVM)分类，完成对城市植被分布信息的精准获取。

1 研究方法

1.1 基于PCA的高光谱图像降维

PCA可以将原始的高光谱图像从多个波段转化为少数几个具有综合性的波段，尽可能去除波段之间的相关性[12]，减少波段的数目，从而实现高光谱图像的降维处理。

给定高光谱图像的样本数为m，波段数目为n，可以用矩阵X来表示此m×n个数据。

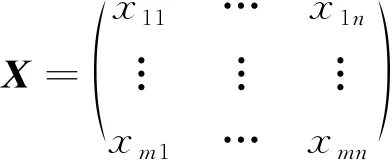
(1)

式中，xmn代表第m个样本中第n个波段的数值。

通过对X进行标准化得到矩阵A；接着，计算A的协方差矩阵R；计算协方差矩阵R的特征值以及相应的特征向量和确定所要降到的低维空间的维数w，从而输出所要的主成分。

1.2 基于t-SNE的高光谱图像降维

t-SNE算法是一种利用概率进行降维分析的方法[13]，它将高维空间中任意两个数据点间的欧氏距离转换为相似概率，并且用高维空间数据点和对应低维空间模拟的数据点之间的联合概率代替了随机邻域嵌入算法(Stochastic Neighbor Embedding，SNE)中的条件概率，从而解决SNE算法中不对称的问题[14]。另外，该算法在低维空间中采用t分布，t分布是一种典型的长尾分布，可以使高维度下中低等距离的数据点在映射后有一个较大的距离，从而有效解决低维空间中数据点拥挤的问题。

对于给定高光谱图像数据X是m行n列的矩阵，它的另一种表现形式{x1,x2,…,xs,…,xm}。式中,xs=[xs1,xs2,…,xsn],s=1,2,…,m。

步骤1计算n维空间下高光谱图像联合概率pef。

n维空间的数据点{x1,x2,…,xs,…,xm}两两之间的相似条件概率pe|f和pf|e：

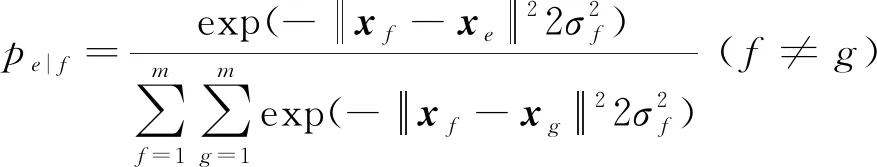
(2)

(3)

式中，σe是以数据点xe为中心的高斯分布的方差。

高维空间联合概率可以表示为：

(4)

步骤2计算低维空间下高光谱图像联合概率qef。

因为t-SNE算法在低维空间采用的是t分布，自由度为1，低维空间的数据点{z1,z2,…,zm}之间的联合分布qef可以表示为

(5)

步骤3计算pef和qef之间的KL散度，将其设为目标函数C，即：

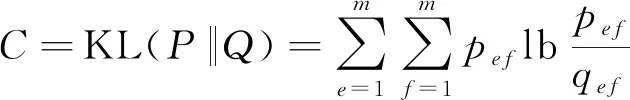
(6)

步骤4用目标函数C对输入数据对应的低维表达式进行求导，如式(7)所示，并把该低维表达式作为可优化变量进行寻优，得到输入值在低维空间内的最佳模拟点。

(7)

步骤5为了获得最小的C，可以对原始数据进行多次的迭代运算，通过不断调整迭代次数n_iter、学习率learning_rate，降低结果的误差。

步骤6定义困惑度perplexity。

由步骤1可知，σe是以数据点xe为中心的高斯分布的方差，任何特定值σe在所有其他数据点上都会诱发概率分布Pe。该分布会随着σe的增加而增加。t-SNE算法使用困惑度perplexity的概念，用二分搜索的方式寻找一个最佳的σe。其中困惑度定义为：

Perp(Pe)=2H(Pe)

(8)

式中，H(Pe)是以比特字节测量的香农熵，

(9)

perplexity是控制拟合的主要参数，会影响高维空间中高斯分布的复杂度，所以需要不断调整perplexity的大小，输出最优的降维结果。

1.3 SVM

SVM的基本思想是寻找一个分类的最优超平面，使得离最优超平面比较近的点能有更大的间距[15]，进而将训练样本中的两类样本能够很好地分开。

支持向量机中的核函数主要有线性核，多项式核，径向基核以及Sigmoid核。在4种核函数中，RBF核函数可以应用到低维、高维、小样本、大样本等情况[16]，所以，本文实验选用径向基函数(RBF)，其核函数如下：

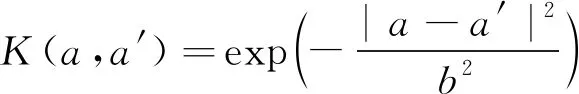
(10)

式中:a为空间中的任意一点;a′为核函数的中心;b为函数的宽度参数。

1.4 基于PCA-t-SNE-SVM的城市植被识别方法

步骤1采用PCA对X进行初步的降维处理，设方差贡献率为95%时，得到d个特征值，将d个特征值对应的特征向量(主成分)作为PCA算法的低维输出数据Y。

步骤2然后，使用t-SNE算法二次降维处理，将d维特征向量映射到s维空间中得到低维数据T。

在实验的过程中，为了提高降维的效果，更好地提取城市植被高光谱图像的本质特征，通过多次试验寻找最优的参数perplexity，learning_rate以及n_iter。

步骤3最后，将降维后的特征矩阵T作为SVM算法的输入矩阵，选取RBF作为核函数，通过gridsearch方法找到最优参数c和gamma，最终得到泛化能力最好的分类结果。

该方法的流程图如图1所示。

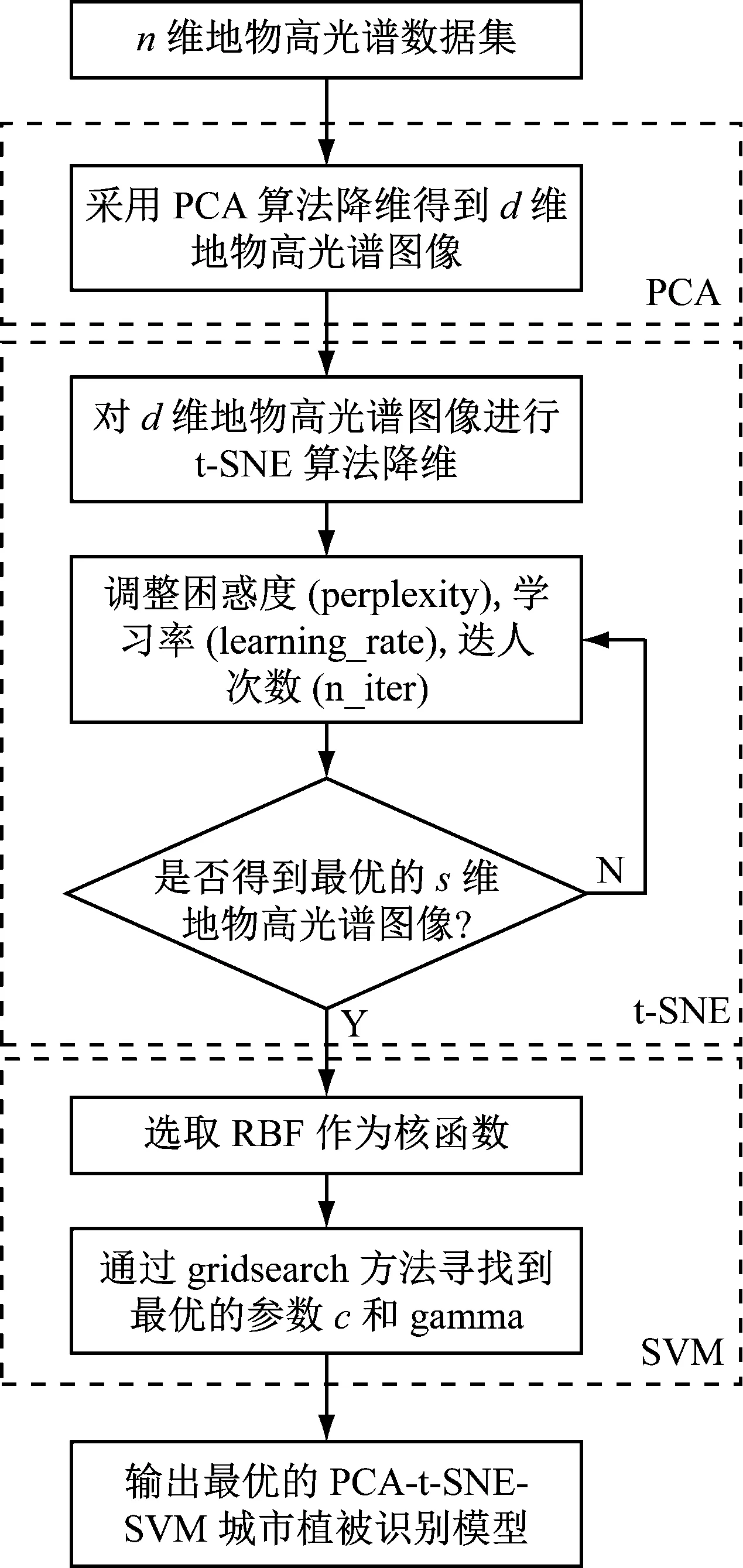
图1 流程图

2 实验结果和分析

2.1 实验数据

采用肯尼迪航天中心(Kennedy Space Center，KSC)的地物高光谱遥感影像数据集为实验对象。该地物高光谱遥感影像大小为512×614像素，其空间分辨率能够达到18 μm，采用的光谱范围为0.4～2.5 μm，共包含了176个波段，影像覆盖了美国Florida Kennedy附近的地物信息。图2是KSC高光谱遥感影像，图3是KSC数据集地物理想分类以及各类地物分布和名称。

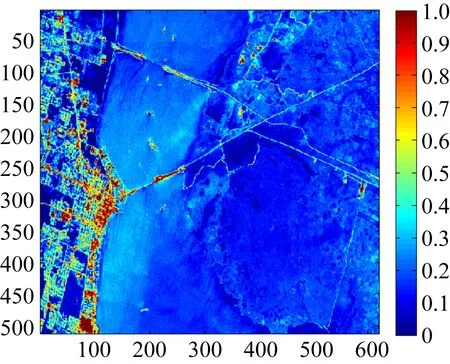
图2 KSC高光谱遥感影像

图3 KSC数据集地物分类及名称

KSC高光谱图像类别信息如表1所示，标记的样本总数为5 211，样本集共13类。

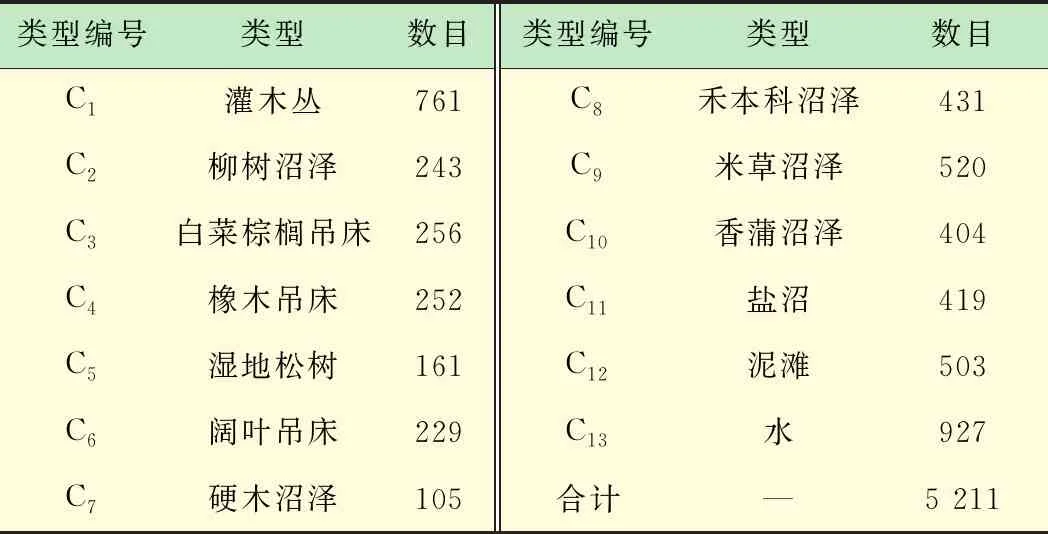
表1 KSC高光谱图像类别信息

2.2 实验结果分析

实验采用的计算机配置是i7-6700 CPU，12 G RAM，软件为Spyder(3.2.6)。

(1) 高光谱图像特征提取。图4是基于PCA算法降维后的可视化结果，从中可以看出，虽然有一部分呈线性分布，但是仍出现严重重叠的情况，无任何规律，没有明显特征和聚类。PCA算法特征提取的运行时间为8 s。

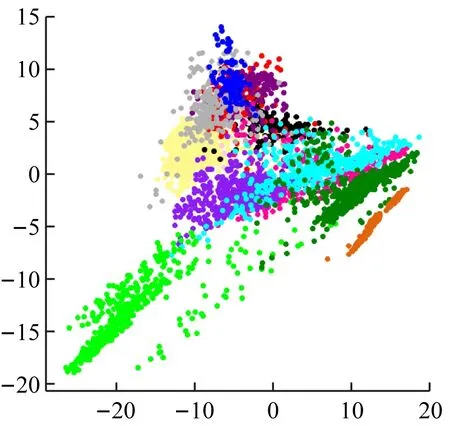
图4 基于PCA算法降维后的可视化结果

图5是基于t-SNE算法降维后的可视化结果。在运用t-SNE进行特征提取时，perplexity，learning_rate以及n_iter会影响降维后的效果和结果的误差。通常情况下，perplexity在5～50之间，learning_rate在10～1 000之间，n_iter至少为250，采用实验方法确定参数的取值，perplexity(per)的值选取为5、30、50，learning_rate(lr)的值选取为10、200、1 000，n_iter(ni)的值选取为250、1 000、3 000，总共对高光谱图像进行了27次的降维试验。图5列出了部分降维后的图像。

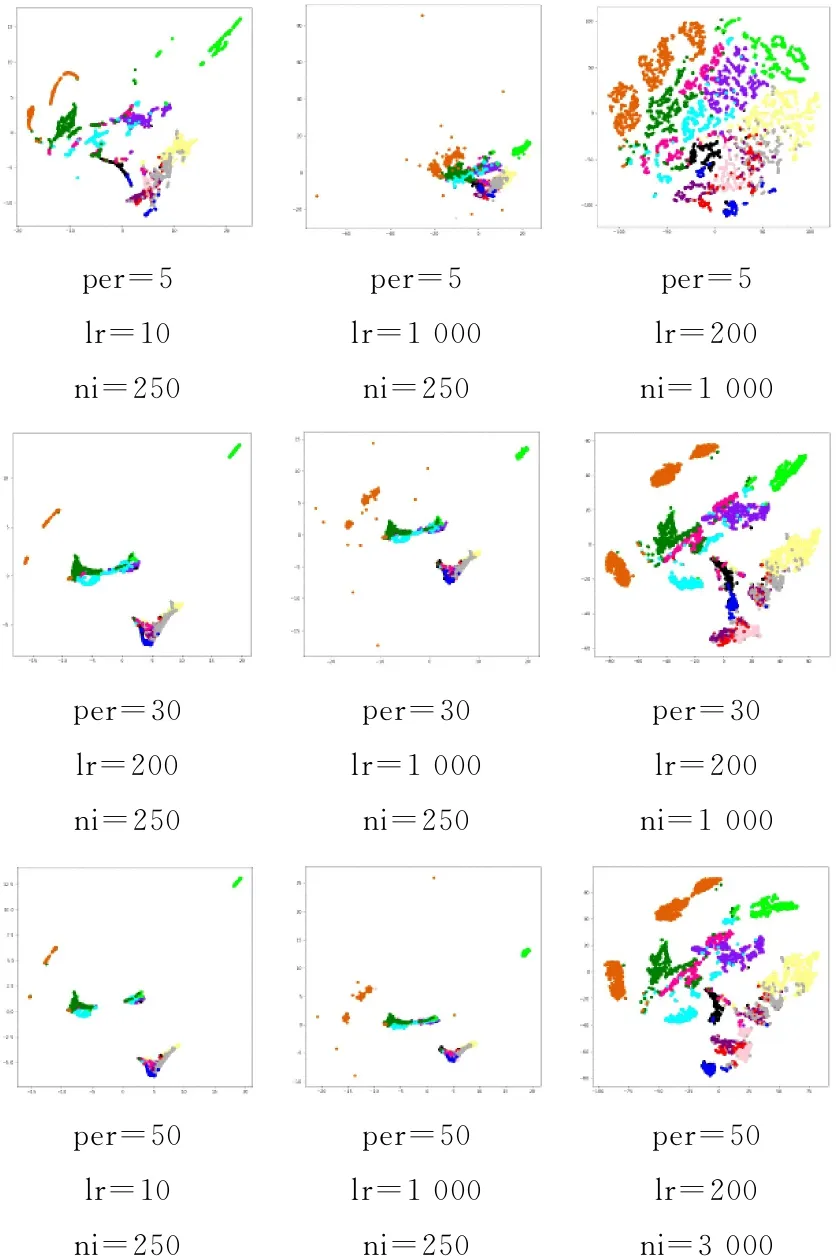
图5 基于t-SNE算法降维后的可视化结果

从图5可以看出，在perplexity=30，learning_rate=200，n_iter=1 000时，同一类之间距离较近，聚集能力较强；不同类之间的距离较远，聚集能力较弱；重叠情况也不是很严重。由此可以看出，在此参数下的降维结果最为理想，t-SNE算法特征提取的运行时间为94 s。

图6是基于PCA-t-SNE算法降维后的可视化结果。首先，采用PCA算法进行主成分分析，表2中显示的是主成分贡献率和累计贡献率的值，可以看到第一阶主成分贡献率最高达到61.1%，此后各阶主成分贡献率逐渐递减，当累计贡献率达到95%时，阶数达到11，从而获取相应的特征向量。

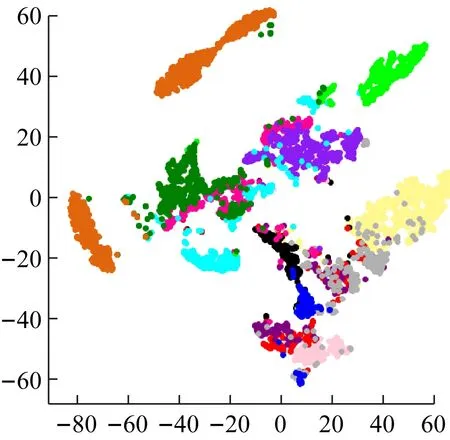
图6 基于PCA-t-SNE算法降维后的可视化结果

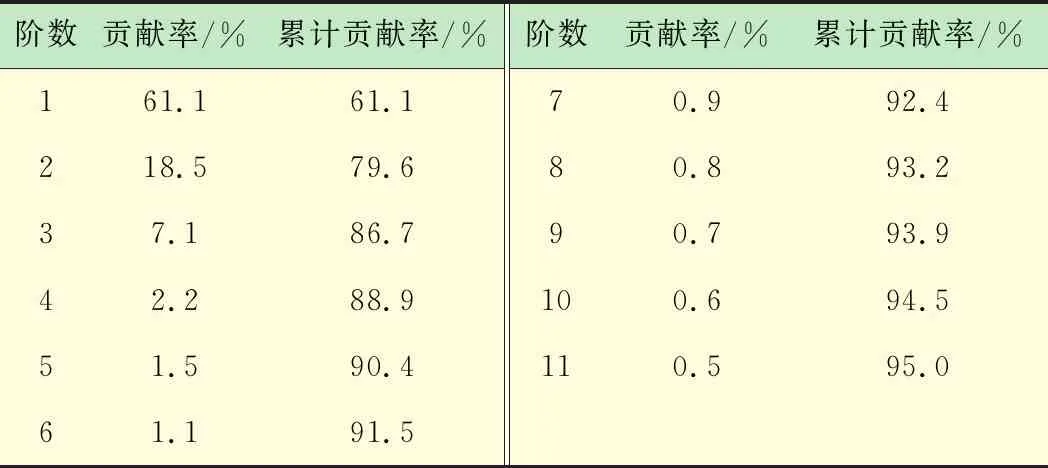
阶数贡献率/%累计贡献率/%阶数贡献率/%累计贡献率/%161.161.170.992.4218.579.680.893.237.186.790.793.942.288.9100.694.551.590.4110.595.061.191.5

其次，运用t-SNE算法再对11维特征向量进行降维处理。在经过27种不同参数组合的试验后，同样在perplexity=30，learning_rate=200，n_iter=1 000时，能很好地提取到高光谱图像的本质特征。由图8可见，类内距离更小，类间距离更大，降维效果较为理想，图6是PCA-t-SNE算法特征提取后的可视化结果，运行时间为46 s。

综上所述，由3种算法的降维运行时间可以看出，PCA算法的运算速率高、运行时间短；t-SNE算法内存占用大、运行速率低、运行时间长；PCA算法与t-SNE算法结合后，可以有效减少降维运行时间，运行时间为46 s，与t-SNE算法相比减少了48 s。

(2) 高光谱图像分类。在样本中随机选取60%的标记样本作为训练样本建立SVM城市植被识别模型，另外40%的标记样本作为测试样本。其中，SVM算法的c和gamma均在{2-10,…,210}范围内，在实验的过程中可以通过gridsearch方法获得相应的最优参数，参数如表3所示。

表3 SVM最优参数

图7是实际分类的效果图，红色框所圈区域为分类错误的主要区域。从图7(a)中可以看出分类的效果不是很理想，存在很多的噪声散点；从图7(b)中可以看出，噪声散点相对减少，分类效果较为理想；从图7(c)中可以看出，噪声散点最少，分类效果最理想。实验表明PCA-t-SNE-SVM具有良好的识别效果。

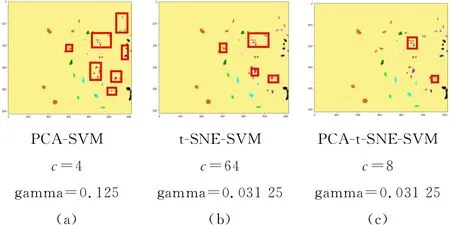
图7 实际分类效果图

(3) 结果分析。OA定义为正确分类的样本数与所有分类样本数的比值。3种算法的OA如表4所示，PCA-t-SNE-SVM的总体分类精度最高，达到92.06%，与PCA-SVM，t-SNE-SVM相比，分别提高了13.51%，3.33%。t-SNE-SVM与PCA-SVM相比，总体的分类精度提高了10.18%。由此可以看出，t-SNE算法可以有效解决数据点在二维空间的拥挤问题，进而提高了高光谱图像的分类精度。

Kappa系数表示的是地物分布结果与真实地物分布之间的相似度。总体分类精度过于依赖类别数和样本，而Kappa系数能够考虑各种漏分和错分的样本。公式如下：

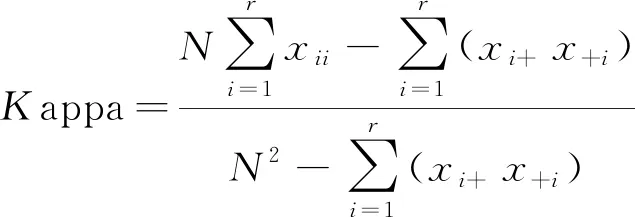
(11)

式中:r为混淆矩阵的行数或者列数;xi+和x+i分别代表各行与各列之和;xii是i行i列(混淆矩阵对角线)的值即被正确分类的样本数。通常Kappa系数在0～1间。

PCA，t-SNE与融合算法下的Kappa系数值如表4所示。由表4可以看出，PCA-t-SNE-SVM错分的样本数最少，Kappa系数最高，达到0.91，与PCA-SVM，t-SNE-SVM相比，分别提高了0.15，0.04。t-SNE-SVM与PCA-SVM相比，Kappa系数提高了0.11。由此可以看出，改进的算法可以有效减少由“同物异谱”或“异物同谱”导致的错分现象的产生，进而提高用于城市植被信息提取的高光谱图像的分类效果。

表4 不同算法的分类结果

Ci为各类别的分类精度。在3种算法下的各类别Ci的分类精度如图8所示，横坐标为类别，纵坐标为各类别Ci的分类精度的百分比。

图8 各类别Ci的分类精度

PCA-t-SNE-SVM最优分类类别的分类精度与最差分类类别的分类精度相差31.58%，而t-SNE-SVM两者相差41.23%，PCA-SVM两者相差79.73%，这一定程度上说明PCA-t-SNE-SVM对类间光谱特性差异性相对鲁棒；从这13类分类性能变化趋势来看，影响分类精度的一个关键因素是地物本身的光谱特性；从这3种分类算法中可以看出，对C1，C11，C13都具有较高的分类精度，而对于C5，C6都具有较低的分类精度。

3 结 语

本文根据PCA与t-SNE的问题及自身的优劣特点，提出了将PCA与t-SNE算法结合对高光谱图像进行降维的方法，并建立了基于SVM的城市植被识别模型。该方法在保留有用信息的基础上，利用PCA算法快速地实现一次降维，应用t-SNE算法二次降维优选出关键特征，运用SVM算法实现城市植被的识别。实验结果表明： PCA-SVM虽然在特征提取的时间上有明显优势，但是对高光谱图像的分类效果不好；t-SNE-SVM可以较好地实现对高光谱图像的分类，但是特征提取时间长，运算速率明显下降；基于PCA与t-SNE特征降维的SVM城市植被识别方法可以有效地提取高光谱图像的本质特征，降低特征提取的时间，提高高光谱图像的分类精度，通过与PCA-SVM和t-SNE-SVM进行比较，验证了特征融合降维方法在时间和分类精度的明显优势。

t-SNE算法中的perplexity，learning_rate，n_iter设置会对降维的效果造成影响，后续将会研究一种最优参数自动匹配的方法，能根据样本的复杂性和特性自动调整参数的大小，从而获得更好的城市植被分类识别效果。