电动汽车用轮毂电机磁热耦合仿真分析

张 琪, 雷良育,2, 靳家宝, 胡 峰, 孙崇昆

(1.浙江农林大学 工程学院，临安311300；2.浙江兆丰机电股份有限公司，杭州 311232)

电动汽车用轮毂电机安装于空间狭小的电动汽车车轮内部，并且汽车正常行驶的道路路况复杂，这样直接使得轮毂电机的散热能力较差[1].高功率密度使得电机温升较高[2],不利于轮毂电机的长期使用[3].所以，较高温升和较差的散热条件，使得对轮毂电机温升的准确计算显得愈发的重要.

目前，国内外学者对电机温升的计算方法主要有3种：①参数计算法；②等效热路法；③有限元分析法.其中，国外的Christian Kral等[4]采用了参数计算法，建立了轮毂电机温度场计算数学模型，虽然计算速度较快，但是不能真实的反应出电机内部的温度分布情况，存在一定误差.国内贾珍珍等[5]运用有限元方法，分析了轮毂电机的温度场分布和温升情况，但是，仅采用了二维平面有限元分析方法，没有考虑电机轴向温度散热能力对电机整体温度的影响；高晓林等[6]运用Fluent流体分析软件对电机的散热进行了分析，但是，Fluent网格划分要求较高，且处理时间较长，对于复杂的电机内部结构，不利于实际工程计算中的效率要求.

为了使温升计算结果较为准确，并且计算效率较高，文中以一台4 kW轮毂电机样机为研究对象，在ANSYS Transient Thermal模块中，以磁热耦合的方式，分析了额定工况下的轮毂电机的整体温度场.为了方便有限元模型的建立，文中提出将轮毂电机内部复杂结构的求解模型进行简化和等效处理，并通过相关流体力学和传热学的公式，计算出散热边界条件来模拟轮毂电机的散热情况，最后,将得出的温度场的仿真结果与试验数据进行对比，验证了所提出的磁热耦合仿真计算方法的正确性，为轮毂电机的冷却结构设计提供重要的参考依据.

1 轮毂电机热性能参数的确定

1.1轮毂电机的基本参数

轮毂电机的基本参数如表1所示.

表1 电机基本参数

电机内部结构较为复杂，结构较为紧凑，散热条件较差.在自然风冷条件下，轮毂电机的主要热交换方式如图1所示，主要由电机内部各部件的传热、电机外部壳体和内部结构的对流换热等组成.

图1 电机内热交换

1.2 热源计算

电磁损耗主要包括定转子铁芯损耗、铜耗和永磁体涡流损耗，电磁损耗是轮毂电机的主要热源，所以，需要准确的计算出电磁损耗的具体数值.通过Maxwell电磁分析软件准确地分析出额定工况下轮毂电机各部件的电磁损耗分布云图.如图2所示，在齿顶处的定子铁芯损耗较大，这是因为此处的磁密较为集中.如图3所示，在齿槽开口处的永磁体涡流损耗较大，这是由于定子槽口的齿槽效应会产生磁场高次谐波，会引起较大的涡流损耗[7].

图2 额定工况定子铁芯损耗分布云图

图3 额定工况永磁体涡流损耗分布云图

经过Maxwell后处理计算模块，得到轮毂电机定、转子铁芯损耗和永磁体涡流损耗具体数值大小，如表2所示.其中，转子的铁耗较小，仅为定子铁耗的0.89%，可以忽略不计，铜耗的数值最大，占总体电磁损耗的一半.

表2 额定工况下电机内各部件的电磁损耗分布

2 轮毂电机温度场分析

2.1 复杂部件的简化与等效

2.1.1 定子槽绕组模型的简化与等效

在建立温度场分析模型时，定子槽中的绕组和绝缘体结构复杂，很难精确的建立有限元模型.可以将绕组等效为一整块导体，绝缘体按体积等效成等体积的包围层，并平行紧贴于槽壁，简化模型如图4所示.

根据传热学定理[8]，通过下列公式计算等效后的绝缘层和导体的物性参数.

图4 定子槽绕组模型等效简化

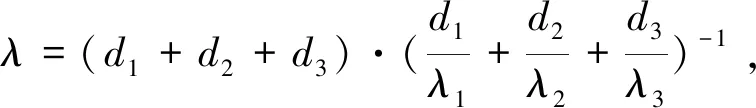
(1)

ds=d1+d2+d3，

(2)

(3)

(4)

式中：d1为定子槽绝缘材料的厚度；d2为槽绝缘材料与定子之间气隙厚度；d3为绕组铜线的绝缘漆厚度；ρ1、ρ2和ρ3为对应的绝缘体密度；c1、c2、c3分别为绝缘体的比热容；v1、v2、v3分别为对应的绝缘体的体积.

结合上述公式，计算得到等效绝缘体的等效结构尺寸和等效物性参数，如下表3所示.

表3 定子槽绕组等效模型的等效物性参数

2.1.2 铁芯叠片模型的等效与简化处理

定子铁芯是由多层硅钢片经过叠压而成，结构比较复杂.可以将铁芯叠片等效成具有轴向、径向和切向不同导热性能的结合体，导热等效示意图如图5所示.

图5 定子铁芯叠片传热等效示意图

可以通过下列公式计算得到定子铁芯在各个方向上的导热系数.

(5)

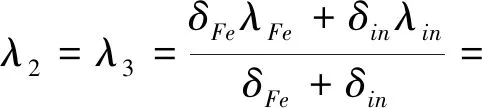
(6)

通过计算得到等效模型物理属性参数如表4所示.

表4 定子铁芯简化模型物理属性参数

为了使温度场分析时的有限元模型更加简单，需要对轮毂电机中温度场分析影响较小的次要部件进行一定的省略和简化，如螺栓、垫片等，并假设保留的主要部件之间是紧密接触无空隙的，最后得到的简化模型如图6所示.

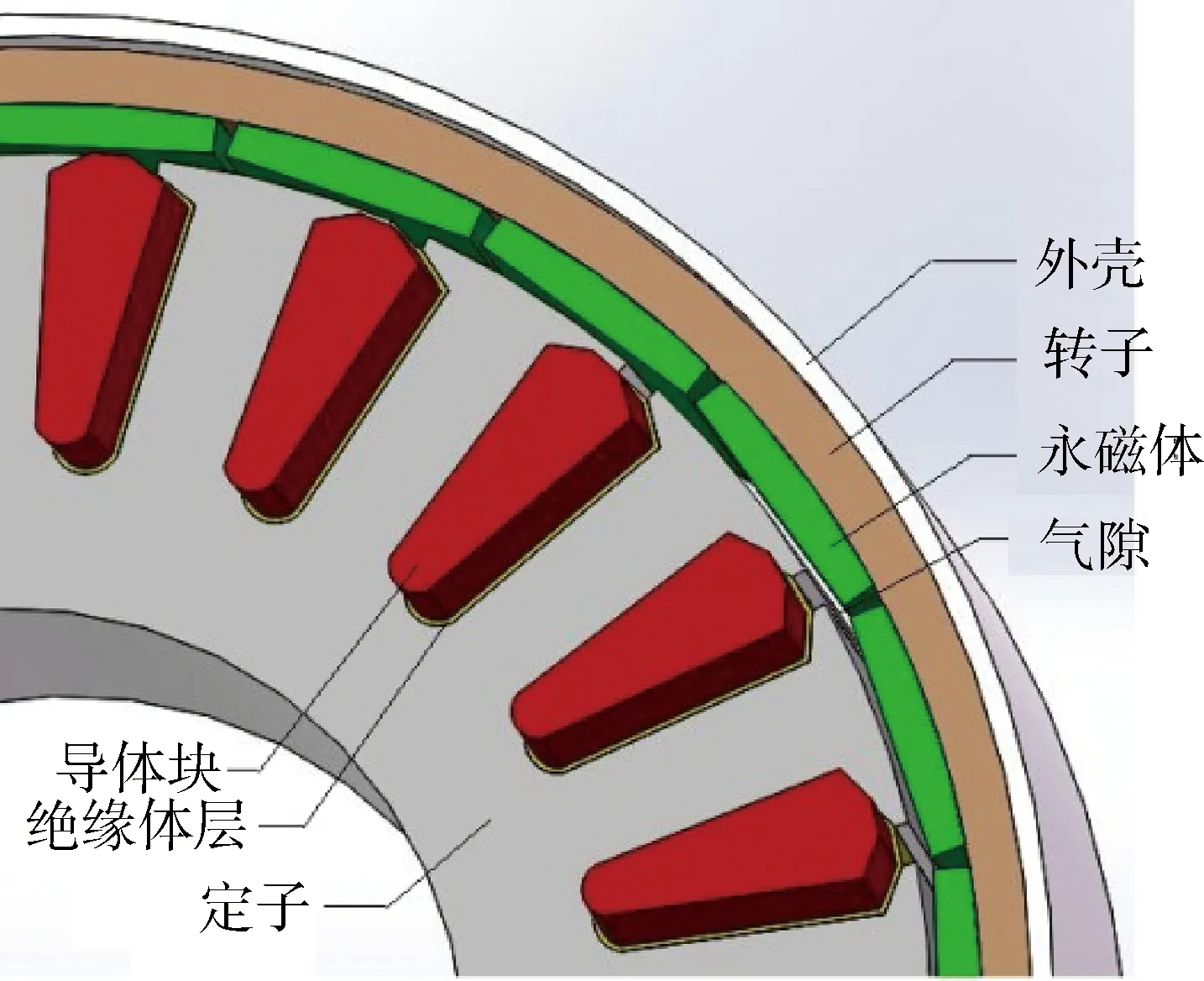
图6 轮毂电机简化模型图

2.2 对流换热系数的等效与计算

轮毂电机主要的对流换热边界面如图7所示，散热边界的数值大小表示轮毂电机各个表面散热能力的强弱，需要精确计算.

2.2.1 气隙散热系数的计算

随着电机转子的旋转，电机气隙中的空气会流动，但气隙的尺寸较小，很难在温度场计算时模拟气隙的旋转和运动，因此，对定转子间的气隙做静止处理，通过公式(7)计算气隙散热系数来模拟气流运动时的散热能力[9].

(7)

式中：hairgap和λair分别为气隙的等效传热系数和空气导热系数；δ为气隙长度；T∂和Pr分别为气隙雷诺数和普朗特数.

2.2.2 轮毂电机外壳表面散热系数的计算

电机壳在旋转时通过对流的形式与外界环境发生热交换，同时旋转外壳会加速周围空气的流动从而增强散热效果[10]，机壳的对流散热系数计算公式如下.

(8)

式中：hca为机壳外表面的对流散热系数；vair为电机壳外表面空气的运动速度，按照电机壳旋转速度的70%取值[11].

根据以上公式计算得到了电机对流散热边界面的散热系数，具体数值如下表所示.

表5 轮毂电机各边界面对流散热系数

3 额定工况下轮毂电机温度场仿真结果分析

进行瞬态温度场求解后，得到额定工况下的轮毂电机运行3 600 s后的温度场分布云图，如图8所示.从温度场仿真结果可知绕组部分的温度最高，因为绕组铜耗最大，绕组最高温度为122.23 ℃，最低温度为121.45 ℃，由于槽绝缘的隔热作用，绕组的最高温度区域出现在绕组中间位置，最低温度区域出现在两端，但是,绕组的温度差异较小，整体温度分布较为均匀.

定子的最高温度区域出现在槽底部与定子轭内圆之间的位置，因为定子的位置与绕组位置最接近，并且定子本身也是发热源，所以，定子的最高温度仅次于绕组，最高温度为120.78 ℃.

永磁体的温差较大，最高温度为118.22 ℃，最低温度为113.24 ℃，由于磁极内圆处接近温度较高的定子，外圆接近散热较好的转子与外壳，所以，磁极内圆与外圆形成了一个4.98 ℃的温差范围.

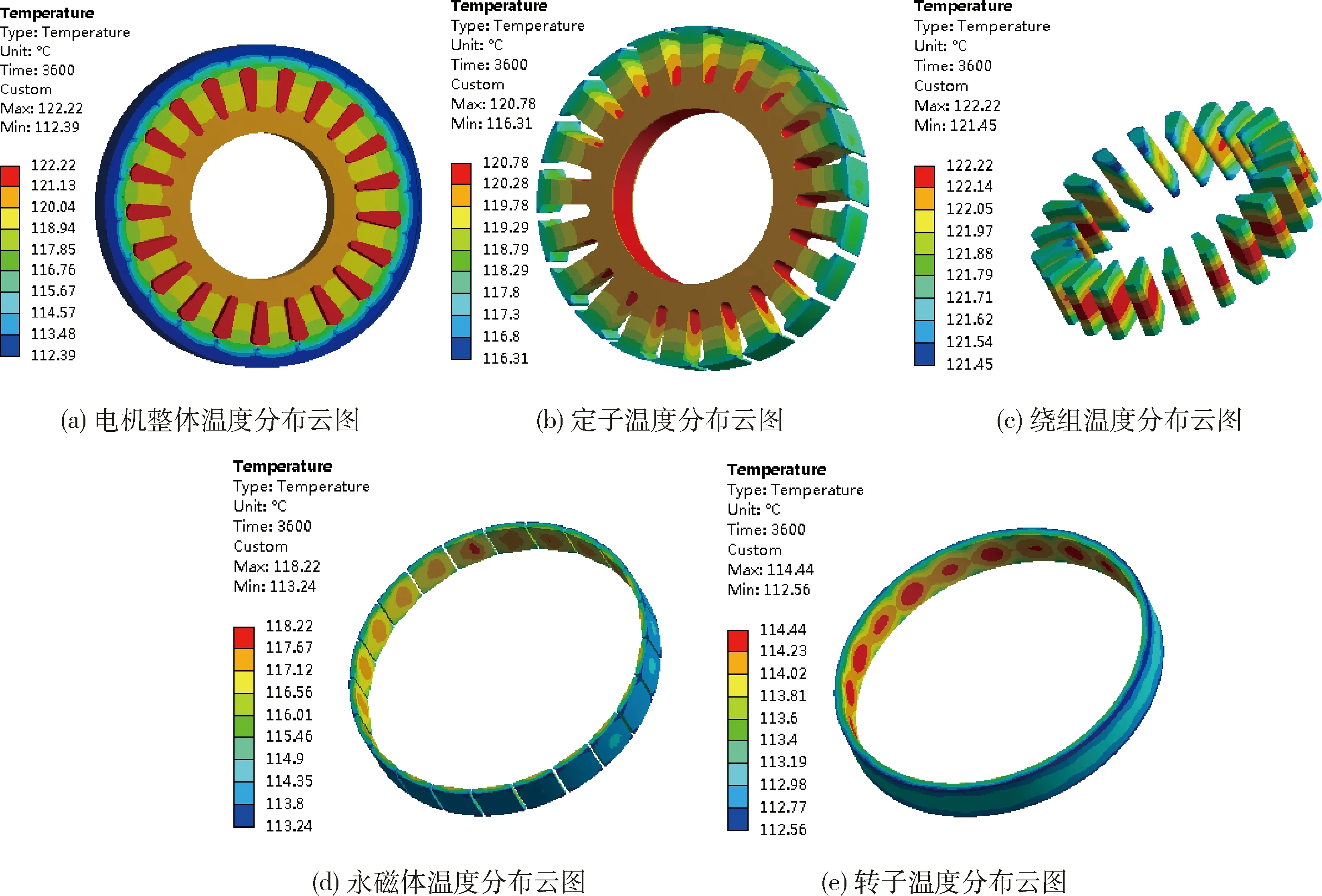
图8 电机整体和各部件温度分布云图

4 试验验证

为了验证文中所述轮毂电机温度场仿真方法的正确性，需要对轮毂电机进行温升试验.试验所用的检测平台为轮毂电机综合性能试验台，如图9所示，该试验台由测功仪、控制器、试验架、温度传感器等部件组成.运用温度传感器埋入绕组端部，以检测绕组端部温度变化，并运用红外温度计测量电机外壳温度.

为了减小试验值和仿真值的误差，需要使试验条件和仿真条件基本相同，控制实验室初始环境温度为22 ℃，在试验过程中运用测功仪和控制器配合，使得轮毂电机在额定负载工况下,连续平稳运行1 h，并以1 min为时间段记录温度数据.将得到的温升试验结果与仿真结果进行对比，对比曲线如图10所示.

由图10轮毂电机温升试验与仿真的对比曲线可知，转子外壳的仿真结果与试验结果几乎一致，误差在2%以内.绕组端部的仿真误差较大，最终稳定时的误差相差约2.2 ℃，但最大误差在5%以下，该结果在工程计算误差的允许范围内.通过与试验结果的比对，验证了文中采用的磁-热耦合仿真计算轮毂电机温度场的方法的正确性，该方法能够运用于轮毂电机初期设计中，并且能为轮毂电机散热结构的设计提供重要的参考依据.

图9 轮毂电机综合性能试验台

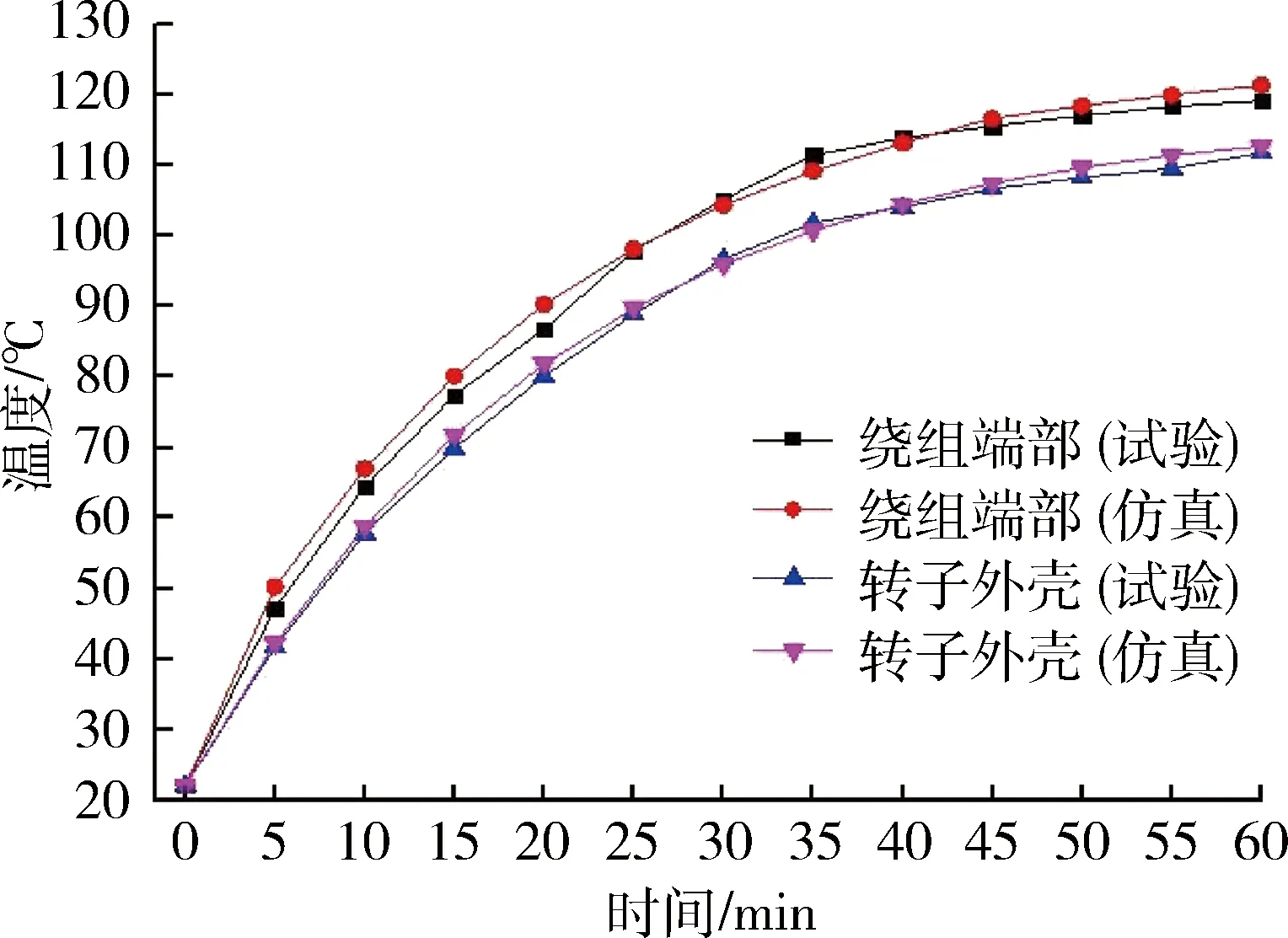
图10 轮毂电机温度试验与仿真对比曲线

5 结 论

通过磁热耦合的方法，对一台4 kW电动汽车用轮毂电机的电磁损耗和温度场进行了研究，得出以下结论：

1)电磁损耗是轮毂电机的主要热源.定子铁芯损耗主要集中在齿顶部位，转子铁芯损耗很小，可以忽略不计，永磁体涡流损耗由于齿槽效应主要集中在定子槽口对应区域.绕组铜耗在总体电磁损耗中所占比例最大，达到了50%，温升最大，所以，在设计散热结构时必须重点考虑绕组区域的冷却效果.

2)在温度场分析模型建立时，绕组部分可以简化成文中提出的导条加绝缘层的模型，硅钢片部分可以简化成一个定子整体，再经过文中给出的传热学相关公式的计算，能够精确的等效计算出简化模型的尺寸和导热系数等参数，等效模型和散热系数的计算是文中提出的磁热耦合分析的关键.

3)从温度场分析结果可知，轮毂电机绕组部位的温度最高，绕组端部温度较绕组中间部位的温度有所降低.由于定子与绕组接触，并且定子部位本身也是热源，所以，定子部位的温度接近绕组部位的温度.永磁体由于靠近转子与外壳，冷却效果较好，永磁体的内层和外层会形成一定温度差.

通过试验分析，验证了结合文中所述的轮毂电机磁热耦合仿真分析方法能够准确的分析出轮毂电机温度场的分布情况，能够为轮毂电机冷却结构的设计提供重要的参考依据.