波流作用下淹没圆柱局部冲深影响因素分析
程永舟,吕 行,王文森,黄筱云,夏 波
(1.长沙理工大学 水利工程学院,湖南长沙 410114;2.水沙科学与水灾害防治湖南省重点实验室,湖南长沙 410114)
近海与海岸工程中运用的桩柱,根据桩高与水深的相对关系,可分为淹没式和非淹没式两种。淹没圆柱在工程领域有广泛的实际应用,例如水下沉箱、重力式锚碇、钻井平台基础、鱼类栖息地等水下淹没结构。淹没圆柱周围的水动力机制与非淹没时有所不同。从水动力角度对波流共同作用下的淹没圆柱周围冲刷深度影响因素进行分析,有助于预报淹没圆柱局部冲深,进而保证其安全建设与稳定服役。
早期研究主要关注波浪、水流单独作用下,非淹没圆柱周围的局部冲刷深度影响因素。Breusers等[1]通过模型试验和现场观测数据对比分析,主要描述了圆柱周围的冲刷发展过程。Melville等[2]研究了均匀海床上,桥墩圆柱基础周围局部冲刷深度随时间的变化规律。Dargahi[3]研究了泥沙粒径、流速和桩径等对水流作用下圆柱周围最大冲刷深度的影响。Sumer等[4]进行了纯波作用下直立圆柱周围局部冲刷试验,提出冲刷深度是KC(Keulegan-Carpenter)数的函数。Sumer等[5]对不同范围KC数纯波作用下,圆柱周围的局部冲刷深度进行了对比分析。结果表明,马蹄涡和尾涡的发展与KC数有密切关系[6],桩周流场极大影响桩柱附近的冲刷[7]。Umeda[8]探究了KC数和Shields参数对波浪作用下平底沙床上桩柱周围局部冲刷的影响。Shields参数可判定冲刷种类,KC数可用于表征桩柱周围涡旋种类与持续时间。纯流作用下,针对淹没圆柱周围的局部冲刷,Zhao等[9]进行了水槽试验与数值模拟,认为随水下圆柱高度减小,马蹄涡与涡脱落减弱是冲刷深度减小的原因。Yao等[10]继续研究类似的问题,分析了纯流冲刷的时间尺度,并提出纵横比这一影响因素进行讨论。Guan等[11]在研究纯流冲刷时进一步考虑了桩基侧向振动的影响。纯流或纯波作用下圆柱周围冲刷机制的相关研究成果,是进一步开展波流共同作用下冲刷研究的良好基础。
波流共同作用时,由于波浪上叠加水流作用,冲刷深度影响因素也有所不同。Sumer等[12]提出Ucw数是波流共同作用下建筑物周围局部冲刷的另一个重要参数。而且,Sumer等[12-13]的试验结果均表明,波流同向作用下桩柱周围的最大冲刷深度,较纯流情形相比,均有所增大。李林普等[14]主要分析和探讨了圆柱直径D、波高H、波长L、水流速度V及海床土体相关参数对大直径圆柱体周围局部冲刷的影响。齐梅兰等[15]通过三维数值模拟,分析KC数、Shields数和Urp数对瞬态孤立波作用下近岸非黏性沙质海床上圆柱体周围局部冲刷的影响。Qi等[16-17]通过波流共同作用下大直径单桩基础周围的局部冲刷试验,主要研究冲刷的发展历时以及相关无量纲参数对平衡冲刷深度的影响。对于大直径小KC数情形下的圆柱周围局部冲刷,研究还不细致。Li等[18]将前述试验发展至双桩情形,并尝试从海床动力响应角度解释冲刷发展过程。Chen等[19]采用表面插入桩,研究了波浪-剪切流作用下的桩身荷载,为进一步开展类似试验提供了借鉴。Welzel等[20]基于导管架波流冲刷试验与单桩情形进行比较,拓展了此类试验的实际利用背景。可见,以往对于圆柱周围最大平衡冲刷深度影响因素研究较多,主要针对于单一影响因素的分析,对于圆柱周围最大平衡冲刷深度的影响因素并没有达成共识,尤其是对于波流共同作用下淹没圆柱冲刷深度影响因素研究较少。
本文基于波流水槽试验,主要考虑Shields数θ,相对流速Ucw,KC数和Fr对淹没圆柱周围局部冲刷深度的影响,并且引入淹没因子Ks,给出淹没圆柱冲刷深度关系式。
1 试验布置与方案
1.1 试验布置
本次试验在长沙理工大学水利实验中心的波流水槽中进行。水槽长45.0 m,宽0.8 m,高1.0 m,水槽工作水深0.2~0.7 m。水槽前端设有造波造流系统,末端设有消能网。圆柱模型埋放在试验段沙槽正中央,沙槽位于波流水槽中段,长3.0 m,宽0.8 m,高0.6 m。沙槽中铺满中值粒径d50=0.22 mm的无黏性沙。波高测量采用WG-50型浪高仪,采样频率为51.2 Hz,精度可达0.4%;流速测量采用三维点式多普勒流速仪(ADV);地形与深度测量采用加拿大2G Robotis公司生产的ULS-100型水下激光三维扫描仪,分辨率为0.018°。具体试验布置见图1。

图1 试验布置Fig.1 Experimental layout
1.2 试验方案
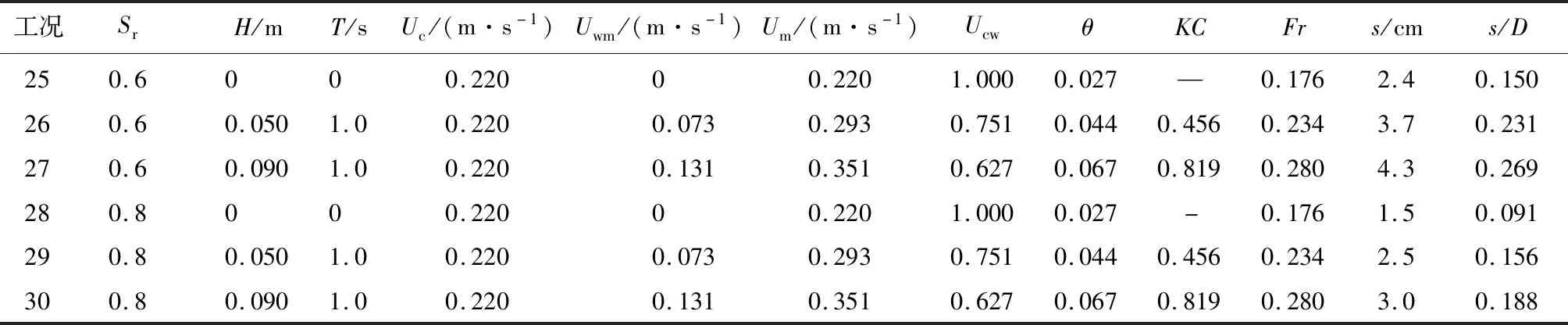
试验中,采用规则波和恒定流作为入射波流,采用间歇式造波法,并且使用浪高仪进行实时监测。模型圆柱直径D=0.16 m,试验固定水深h=0.40 m,不同淹没圆柱高度用淹没率Sr表示,淹没率Sr=(h-hc)/h,h为水深,hc为柱高。需要指出的是,根据直径与波长比值D/L判断,波流试验工况D/L>0.1,属于大直径情形。现场观测数据也关注大直径桩柱与小KC数情形的冲刷[21-22],设置工况时0.435 (1) 式中:Uf为波流共同作用下的最大摩阻流速。临界希尔兹数θcr计算式如下: (2) 式中:D*=d50[(s-1)g/υ2]1/3为沙粒无量纲粒度。本次试验中临界希尔兹数θcr=0.045。相关无量纲参数KC,Fr和Ucw表达式如下: (3) (4) (5) 式中:Uwm为距离床面1.0D处纯波浪水质点运动的最大流速,Um=Uc+Uwm表示波流作用时水下距离床面1.0D处的最大流速,Uc表示水下距离床面1.0D处的纯水流流速;D为圆柱直径;T为周期。 表1 试验工况Tab.1 Experimental conditions (续表) 图2给出Sr=0.4,H=0.09 m,T=1.0 s,Uc=0.220 m/s时冲刷发展接近平衡时的地形照片,t表示冲刷时间。通过图2可以发现,冲刷坑主要由柱前的半环状冲刷坑、侧坑和斜后方的冲淤相间区及运动的淤积区组成。在马蹄涡的作用下,柱前半环状冲刷坑边坡泥沙颗粒不断脱落,半环状冲刷坑持续展宽。冲刷接近平衡时,冲刷坑边坡接近泥沙休止角,坡上泥沙颗粒不再移动。淤积区一直紧靠圆柱侧后方动态变化,归因于大直径圆柱绕流作用较大,卷起的泥沙绕圆柱向柱后移动,最终两侧的淤积合并成一个大规模沙丘。直至冲刷准平衡,桩周地形不再发生显著演化。总体来看,冲刷坑对称性良好,最大冲深保持在圆柱侧前方45°。最终,圆柱后方淤积成一个“马鞍状”沙丘。 图2 冲刷准平衡地形Fig.2 Quasi-equilibrium scour topography 图3 相对冲刷深度s/D与Ucw的关系Fig.3 Relationship between s/D and Ucw 波流共同作用条件下,相对流速Ucw可表征波流共同作用时的流速。相对流速Ucw的范围为0~1。其中,Ucw=0表示纯波作用,Ucw=1表示纯流作用。图3为相对冲刷深度s/D与Ucw的关系。 Sr=0.4时,如图3所示,当KC数保持不变时,相对冲刷深度s/D随着相对流速Ucw的增大而增大,但是增大速率逐渐降低。KC数较小时,曲线增长速率越快;KC数较大(KC=1.181)时,相对流速Ucw最小,而冲刷深度也能达到较大的数值。这说明,即使在波浪上叠加较小的水流,也会导致冲刷深度显著增加。此时,水流在柱前生成强大的马蹄形涡,即使弱流情况下也出现。在马蹄涡控制下,弱流强波的组合也会产生较大的冲刷深度。根据Sumer等[12]的研究可知,此时冲刷深度明显由组合流的水流分量控制,较大的Ucw情况下,圆柱上游侧的尾涡基本完全消失,导致较大的Ucw时冲刷深度反而偏小。 图4 相对冲刷深度s/D与KC数的关系Fig.4 Relationship between s/D and KC 图4给出的是相同淹没率(Sr=0.4)情况下,不同相对流速Ucw时相对冲刷深度s/D与KC数的关系。同时,将淹没圆柱试验结果与Qi等[16]试验结果平滑连接。如图4所示,冲刷深度s/D随KC数的增加而增加,增长速率趋缓。在不同的Ucw范围内,每条冲刷深度与KC数的趋势线不同,当KC数增加到3左右时,KC数与冲深s/D趋于平稳,达到渐进值。对比3条不同的冲刷深度s/D与KC数趋势线可以看出,在Ucw=0.60~0.70和Ucw=0.70~0.80相对流速较大的条件下,曲线的快速增长阶段增长速率明显小于较小的相对流速Ucw=0.50~0.60。这从另一个角度说明了弱流强波组合也可能产生较大冲刷。这是由于冲刷深度s/D主要受相对流速Ucw控制,水流流速的轻微增加,即导致冲刷深度的显著增加。 图5 相对冲刷深度s/D与Fr数的关系Fig.5 Relationship between s/D and Fr 图5给出了相同淹没率(Sr=0.4)情况下,相对冲刷深度s/D与Fr的关系,图中还给出了Sumer等[12,16]的圆柱冲刷试验结果。从图5可见,相对冲刷深度s/D随着Fr的增大而增大,对于小KC数情况下增长幅度比较大,当增大到一定程度时(Fr>0.80),相对冲刷深度s/D达到一个渐进值,约等于2。当Fr>0.80时,接近纯水流作用,Fr数基本上代表了桩周围的流动梯度,马蹄涡和下降流的形成也与其有关。Qi等[16]的试验研究认为,尽管KC值、水深和粒径大小的范围不同,冲刷深度数据可以用以下经验式表达: lg(s/D)=-0.8exp(0.14/Fr)+1.11 (0.10 (6) 对于本试验数据,当0.20 图6 相对冲刷深度s/D与淹没率Sr的关系Fig.6 Relationship between s/D and Sr 本次试验共选用了5种不同淹没高度的圆柱。图6给出了相同波流情况下不同淹没率圆柱周围冲刷深度。如图6所示,随着淹没率Sr的增加,也就是桩高降低,相对冲刷深度s/D减小。保持桩径不变,通过示踪剂观测试验现象,可明显看出桩周涡系统的强度随着淹没率Sr的增加而减小。因此,波流共同作用下淹没圆柱周围冲刷深度s/D随着淹没率Sr的增加显著减小,此变化趋势与Dey等[23]纯流情况的研究结果一致。 图7 淹没因子Ks与淹没率Sr的关系Fig.7 Relationship between Ks and Sr 对于淹没圆柱周围的局部冲刷研究,如2.5节所述淹没率是影响冲刷深度的重要因素。通常认为可将淹没柱体的冲刷深度与相同直径的未淹没柱体的冲刷深度相关联,Dey等[23]研究恒定流作用下淹没圆柱结构周围局部冲刷时引入了淹没因子Ks,淹没圆柱冲刷深度可以表示为: s/D=Ks·s0/D (7) 式中:淹没系数Ks为淹没圆柱体的冲刷深度与等直径未淹没圆柱体的冲刷深度之比;s0为未淹没圆柱的冲刷深度。图7拟合得到的Ks与淹没率Sr的关系曲线为Ks=1-0.641 2s+0.902 7s2-1.258 4s3,相关系数R2=0.994 9。当s=0时,Ks=1表示非淹没圆柱,以及当s=1时,Ks=0表示与床面高度合并的完全嵌入沙床的圆柱。可以发现淹没因子Ks随淹没率Sr的增大而逐渐减小,当Sr增大时,圆柱高度hc减小,从而阻塞流动面积减小,导致淹没圆柱桩相对冲深随淹没率的增大而减小。 基于波流水槽试验,研究了波流共同作用下淹没圆柱冲刷深度影响因素。探讨了无量纲参数θ、相对流速Ucw、KC数、Fr数和淹没率Sr对淹没圆柱周围准平衡冲刷深度的影响,并且引入淹没因子Ks,给出淹没圆柱与非淹没圆柱冲刷深度计算式。主要结论如下: (1)当KC数保持不变时,冲刷深度s/D随着相对流速Ucw的增大而增大。即使较小的Ucw数值时,冲刷深度也能达到较大的数值。 (2)处于相同相对流速Ucw范围内时,冲刷深度s/D随KC数增加,增长速率趋缓。在不同的Ucw范围内时,当KC数增加到3左右时,KC数与冲深s/D趋于平稳,达到渐进值。 (3)相对冲刷深度s/D随着Fr数增长对于小KC数情况下增长幅度比较大;当增大到一定程度时(Fr>0.80),s/D达到一个渐进值,约等于2。 (4)引入淹没因子Ks,得到了淹没圆柱与非淹没圆柱冲刷深度计算式,同时依据试验数据拟合得到了淹没因子Ks与淹没率Sr的关系曲线。
2 试验数据分析
2.1 平衡冲刷坑形态

2.2 相对流速Ucw对相对冲刷深度s/D的影响

2.3 KC数对相对冲刷深度s/D的影响
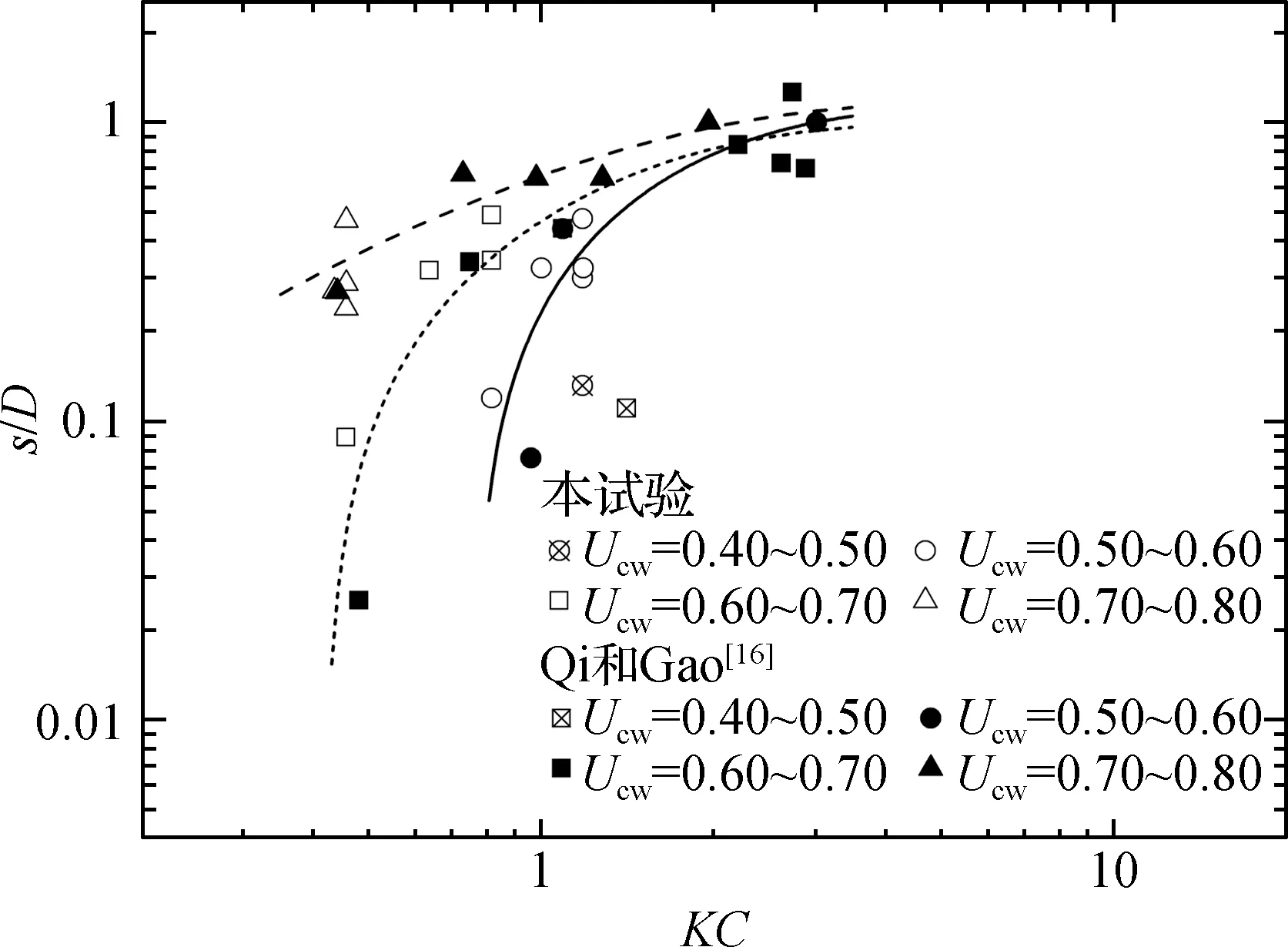
2.4 Fr对相对冲刷深度s/D的影响
2.5 淹没率Sr对冲刷深度s/D的影响

2.6 淹没圆柱冲刷深度关系式

3 结 语

