深水钻井隔水管下放试压单元智能优化

刘 康, 陈国明, 畅元江, 柳 磊, 温纪宏, 胡东旭

(1.中国石油大学(华东)海洋油气装备与安全技术研究中心,山东青岛 266580;2.中海油田服务股份有限公司钻井事业部, 河北三河 065201)

深水钻井隔水管系统是连接海底井口与浮式平台的纽带,也是深水钻井区别于陆地作业的关键装备[1]。隔水管系统由多个相对独立的单根首尾衔接而成,以适应不同井位水深的作业需求[2-3]。隔水管主管连接时,周边辅助管线无法实现螺纹密封,通常采用插入连接的方式。隔水管辅助管线的连接失效,不仅会导致钻井作业被迫停止,增加非生产时间和经济成本,还可能因管内液体泄漏而造成环境污染。因此在隔水管下放过程中需对节流、压井等辅助管线进行试压,以保证隔水管系统的密封安全性。目前,美国石油学会标准API RP 16Q建议5根隔水管单根为一个试压单元[4],Cameron公司隔水管操作手册则建议每下放3根单根便需要进行一次试压作业。随着作业水深的增加及连接可靠性的提高,按照现有规范或相关手册进行作业,试压次数多、耗时长,显然已不是最佳方案。当前国际油价相对低迷、钻井平台综合日费高昂,深度挖掘降本增效空间,保障隔水管下放作业的安全与高效显得尤为重要。然而,深水钻井隔水管下放试压方案的风险值难以量化、效益函数不易确定,最优试压方案的求解为高维度的复杂非线性规划问题。通过调研,国内外针对隔水管下放试压优化的研究鲜有报道,但风险决策理论与智能优化方法发展为该问题的研究奠定了基础。笔者依据风险决策理论建立深水钻井隔水管下放试压时效评估模型与风险计算模型,形成基于蜂群算法的深水钻井隔水管下放试压智能优化方法,确定示例井中隔水管下放试压的最优位置,并从连接可靠性、井位水深两个角度开展影响因素分析,以期为深水钻井隔水管下放试压的优化决策提供理论支持。

1 隔水管下放试压单元评估模型

1.1 下放试压工艺

辅助管线一般通过支架固定在隔水管主管的外侧,是隔水管单根不可分割的部分。隔水管下放试压的主要目的是检验隔水管辅助管柱插入连接的密封性能。隔水管下放试压的现场作业如图1所示。此时隔水管悬挂于浮式钻井平台,作业人员安装好试压工具后,通过水下试压泵依次对各辅助管线进行高、低压测试。低压测试时间相对较短,压力通常约为2 MPa;高压测试时间相对较长,压力依据管线的不同而有所差异,其中阻流/压井管线的压力可高达85 MPa。

试压合格后,则认为此试压单元隔水管辅助管线之间连接密封安全。若试压不合格,则需要将此试压单元的隔水管单根依次起出,检测后重新下放并试压,直至试压合格为止方可下放下一组试压单元的隔水管单根。参考现场作业程序,将隔水管下放试压过程按照自下而上的试压单元进行阶段性分解,绘制隔水管下放试压作业流程如图2所示。图2中隔水管下放试压作业起始于第一个试压单元(最底部试压单元)隔水管单根的下放,终止于最后一个试压单元(最顶部试压单元)隔水管单根的下放完毕且试压合格,各阶段作业流内部构成循环,每次试压失败会导致本阶段隔水管单根的重复性作业,但不同阶段作业流单向流动不可逆转。

图1 隔水管下放试压现场作业图Fig.1 Photo of field pressure test in riser running

图2 隔水管下放试压作业流程Fig.2 Flow chart for pressure test in riser running

为进行隔水管下放试压智能优化分析,假设:

(1)隔水管下放过程中,试压位置可进行随机选择,但不能进行重复的试压作业,即同一个试压位置不能进行连续两次及以上的试压作业,隔水管单根全部下放完毕后必须进行一次试压作业。

(2)隔水管单根的下放回收时间,受到作业设备、单根类型、熟练程度、作业天气等因素的影响,本文考虑隔水管单根在井口的平均占用时间,并做下放、回收作业类型及裸单根、浮力单根类型的区分。

(3)隔水管单根的连接密封可靠性是指两根隔水管单根辅助管线一次连接作业即获得密封成功的概率,可依据现场经验获得,也可依据作业现场的实践进行动态更新。

(4)试压合格,则认为此试压单元隔水管辅助管线之间的连接密封可靠;若试压不合格,需将此试压单元的隔水管单根全部上提并检验,而不考虑已试压合格隔水管单元的影响。

1.2 时效评估模型

深水油气勘探开发是公认的高风险、高投入行业[5-6],如“海洋石油981”钻井平台的综合日费就高达数百万元。建立深水钻井隔水管下放试压时效评估模型是试压优化决策的关键。由于隔水管系统下放作业的整体耗时受到单根密封可靠性的影响,每次单根连接过程中均存在决策者无法控制的成功与失败两种自然状态,隔水管下放试压位置的确定是一个典型的风险性决策问题[7]。期望值法是处理风险决策问题的常用方法,深水钻井隔水管下放试压时效评估模型即是对隔水管系统下放时间期望的数学表征。以隔水管试压单元为分析对象,建立第k个试压单元隔水管全部成功下放的时间成本期望Tk数学模型,表示为

(1)

由Φj和Yi的逻辑关系可知,当且仅当c个隔水管连接位置的Yi全部取1时Φj取0,因此:

(2)

将式(2)代入式(1)可得

(3)

由于下放试压单元相互独立,针对整个深水钻井隔水管系统的下放试压过程有

(4)

其中

式中,n为试压次数;T为隔水管全部下放试压作业成功完成的时间成本期望,h;TF为隔水管全部下放试压作业的固定投入时间成本,h;TR为隔水管全部下放试压作业的安全投入时间成本,h;TL为隔水管全部下放试压作业的失效损失时间成本,h;TE为隔水管全部下放试压作业的安全效益期望时间(安全投入与失效损失的时间成本之和),h。

1.3 风险计算模型

若把深水钻井隔水管下放试压全过程作为一个安全系统分析对象,则每个下放试压单元均是一个安全子系统。钻井隔水管下放试压的整体安全程度由各子系统的安全程度联合决定,试压单元的划分影响了下放试压程序整体安全程度的高低。直观而言,增加下放试压次数、合理选择试压位置有利于控制下放试压过程的作业风险,提高作业程序的整体安全水平。

熵作为描述复杂系统状态的物理量,是系统无序性或不缺确定性的一种表征[8]。Shannon采用信息熵表征信源的不确定性程度,并给出信息熵的数学表达式。Lü等[9]借鉴熵理论形成复杂安全网格脆弱路径的识别方法。Mohsen等[10]基于熵理论形成一种风险权重确定方法。隔水管下放试压风险与熵的演变及耗散过程具有一定的共性,试压单元存在“合格”与“不合格”两种不相容的状态,这种不确定性属于典型的二项分布。下放试压次数的增加,增加了隔水管下放试压过程的可靠性与有序性,属于熵减的过程,在人为干预作用下系统从无序向有序转化。采用风险熵对下放试压作业的安全程度进行量化表征:

h(β)=(β-1)lnβ.

(5)

式中,β为(子)系统可靠度;h(β)可靠度对应的风险熵。

可靠度β的阈值范围为(0,1),风险熵的阈值范围为(0,+∞);概率空间的可靠性指标与熵空间风险熵属于一一映射关系,风险熵随着可靠度的增加单调减小;可靠性较高时风险小,即系统的有序程度高、不确定性低,系统的风险熵也较小,这与熵的基本内涵一致。因而,提出的风险熵可作为深水钻井隔水管下放试压系统风险的度量。

利用熵空间的可加性,形成隔水管下放试压全过程的总熵计算模型,表示为

(6)

式中,βi为第i个试压单元可靠度;ci为第i个试压单元的连接次数。

2 隔水管下放试压单元优化方法

2.1 模型转换与求解思想

人工蜂群算法(artificial bee colony, ABC)是基于蜂群采蜜过程提出的一种仿生学群体智能优化算法,适合于处理高维极值优化问题,目前已在众多领域成功应用[11-14]。蜂群算法中蜜源代表解空间内的可行解,适应度函数用于衡量蜜源质量的优劣;采蜜蜂、观察蜂、侦察蜂3种蜂种进行群体智能的协同寻优。其基本寻优思想描述如下:采蜜蜂与具体的蜂源联系在一起,并依据记忆在邻域内搜索,不断更新蜜源质量;观察蜂通过蜜源质量对食物进行选择,按照一定概率选择蜜源并在其领域内搜索;侦察蜂随机搜索新的可行解,发现新的蜜源位置;找到优质蜜源的观察蜂、侦察蜂转化为采蜜蜂,采蜜蜂在邻域进行一定次数搜索后若不能提高蜜源质量则转化为侦察蜂;迭代过程中3种蜜蜂不断影响与转化,蜂群搜索的蜜源质量不断提高。

2.2 优化模型与计算说明

若存在m个隔水管单根,则每次下放完成一根单根均有一次试压机会,定义蜜源为向量形式:

X={x1,x2,x3,…,xm}.

(7)

式中,xi为第i个单根下放后是否试压的标识,若试压则取1,否则取0。

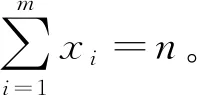
深水钻井隔水管下放试压单元优化的目标是下放作业时间与作业风险(即风险熵)最小,表示为

miny=F(X)={T(X),H(X)}.

(8)

当试压次数n不确定时,上述问题是典型的多目标规划问题,该问题存在Pareto最优解集;当试压次数n确定时,通过试算分析可知下放时间期望与风险熵具有一致性,即两者同时增加或减小。为方便计算分析,可将该问题转化为确定试压次数n的单目标优化问题,设置适应度函数为时间期望与风险熵之积,表示为

(9)

适应度函数值越小时蜜源的质量越高,观察蜂对蜜源的跟随概率越大,令跟随概率为

(10)

式中,Proi为第i个蜜源位置采蜜蜂被跟随的概率;fiti为第i个蜜源的适应度。

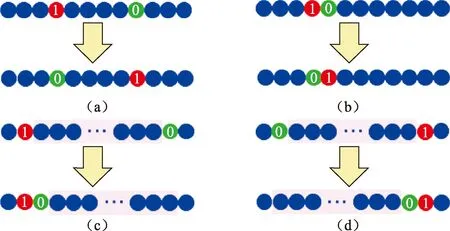
图3 人工蜂群算法搜索策略示意图Fig.3 Search strategy of ABC

蜂群的探索能力与开发能力决定了智能优化算法的优化效率与效果。采蜜蜂的邻域搜索策略如图3(a)和(b)所示,策略一是随机搜索一个1与一个0,两者进行互换;策略二是随机搜索一个1,并与相邻的一个0进行互换。观察蜂的邻域搜索策略如图3(c)和(d)所示,策略一是随机搜索两个位置,将两个位置间的编码右移一位;策略二是随机搜索两个位置,将两个位置间的编码左移一位。策略一、策略二邻域搜索新个体的适应度与原个体适应度进行对比,取最优者进行更新。为保证试压次数n确定时侦察蜂新个体的有效性,其搜索策略采用随机背包算法实现,即在新蜜源向量中随机选择n个互不相同的位置,设置为1(试压位置),其他位置设置为0。

3 应用实例与讨论

图4 最优适应度搜索曲线Fig.4 Search curve of optimal fitness

由图4可知,蜂群的最优适应度函数值随着迭代次数增加逐渐减小,当迭代128次时蜂群获得最优解,其适应度函数为61.277。此时最优的隔水管下放试压单元序列为[10 9 10 9 10 10 9 10 9 9 9 10 10 9],即首先下放10根隔水管单根试压一次,然后依据优化序列依次下放9根或10根进行试压。蜂群的最优适应度函数值在前30代快速地收敛,从30代以后适应度已接近最优值,说明隔水管下放试压单元优化模型具有较好的全局寻优能力。选择3个蜜源绘制适应度变化曲线如图5所示。由图5可知,3个蜜源的适应度均循环出现跳动增加逐步减小的趋势,这是由于蜜源停留超过限制次数时,采蜜蜂转化为侦察蜂,以探索新的蜜源位置,避免种群陷入局部最优解,保障了种群具有较好的探索能力。

图5 蜜源适应度变化曲线Fig.5 Curve of fitness for nectar sources

将优化结果与通用做法进行对比分析,结果如表1所示。分析表1可知,按照Cameron隔水管操作手册下放试压次数最多,安全投入的时间成本也最多,虽然失效损失的时间成本有所降低,然而在同样隔水管配置情况下总的期望作业时间仍然最高。按照API规范推荐做法可节约期望时间31 h,按照ABC智能优化计算结果可节约期望时间44 h。按照目前半潜式平台高达数百万元的综合日费进行测算,依据ABC优化结果开展隔水管下放试压作业有望节约可观的钻井成本。

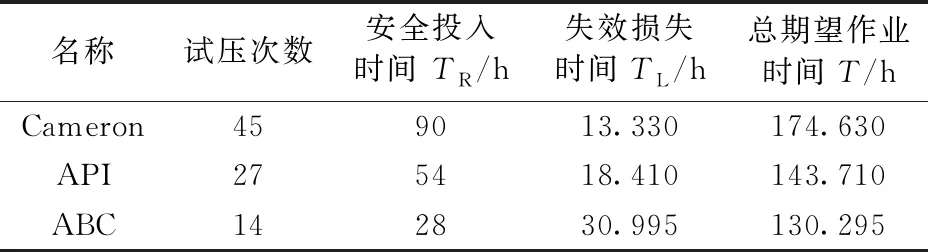
表1 优化结果与通用做法对照Table 1 Comparison of optimization results and common practices

为进一步分析不同试压次数(n)情况下期望作业时间、试压风险的变化规律及相互关系,分析6～36次试压的最优结果,列举部分试压次数与期望时间对应数据如表2所示,绘制不同试压次数下的风险熵与可靠度的变化曲线如图6所示,隔水管下放试压安全效益曲线如图7所示。

表2中总期望作业时间分为固定投入时间、安全投入时间和失效损失时间3部分,其中固定投入时间是指将全部隔水管单根一次性全部连接下放所需要的必要投入时间,由于测试分析的隔水管配置相同,不同试压次数下的固定投入时间一致;安全投入时间是指为了减少失效损失而投入安全保障措施(试压作业)所占用的时间,随着试压次数增加而线性增加;失效损失时间是指密封失效事故损失时间,即一旦发现密封失效,重新起下隔水管消耗的期望时间,随着试压次数的增加,下放试压单元所含的单根数目减小,降低了隔水管连接密封失效后的时间损失。

表2 试压次数与期望时间对应Table 2 Expected time under different pressure test numbers

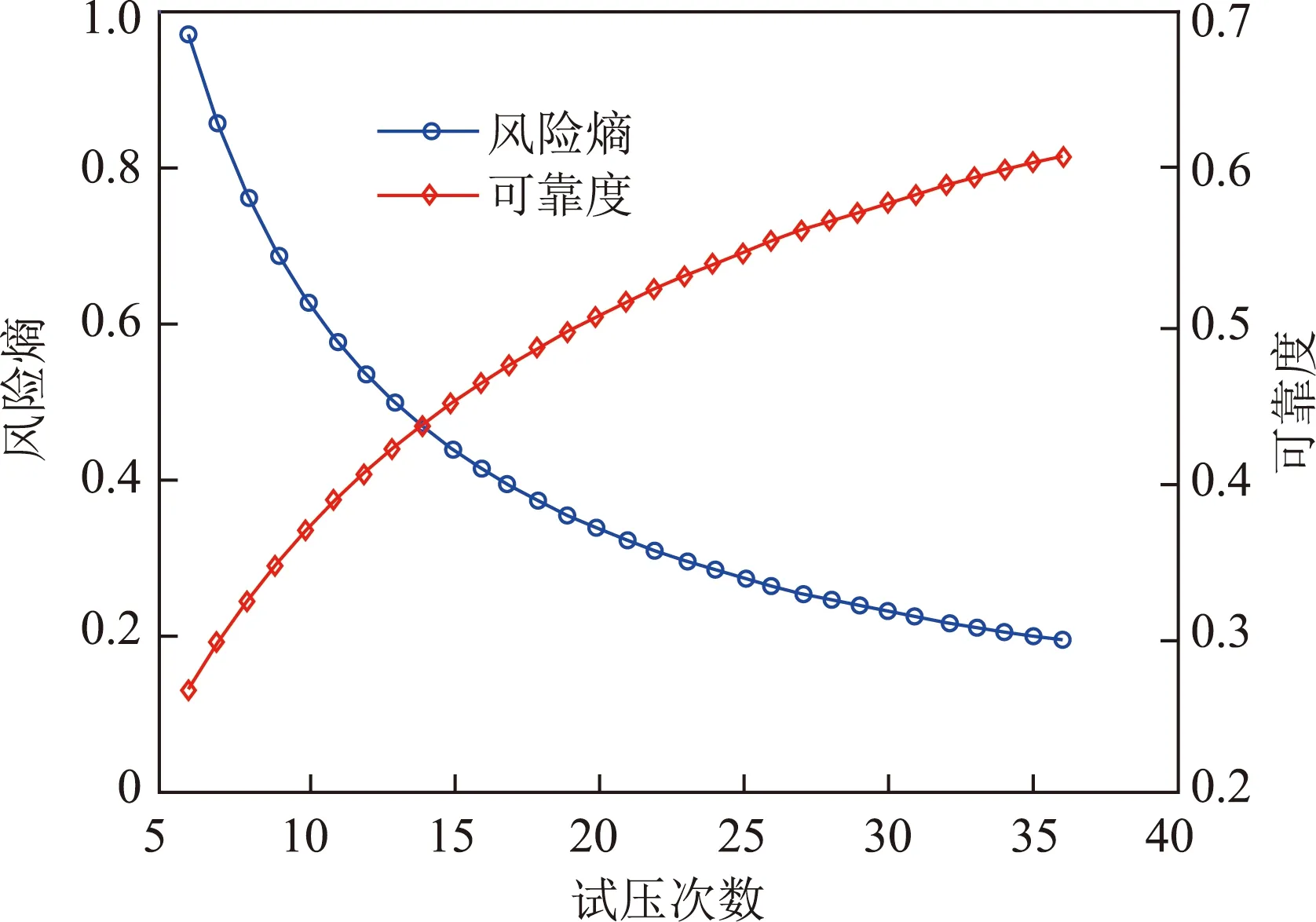
图6 不同试压次数下的风险熵与可靠度Fig.6 Risk entropy and reliability under pressure test number

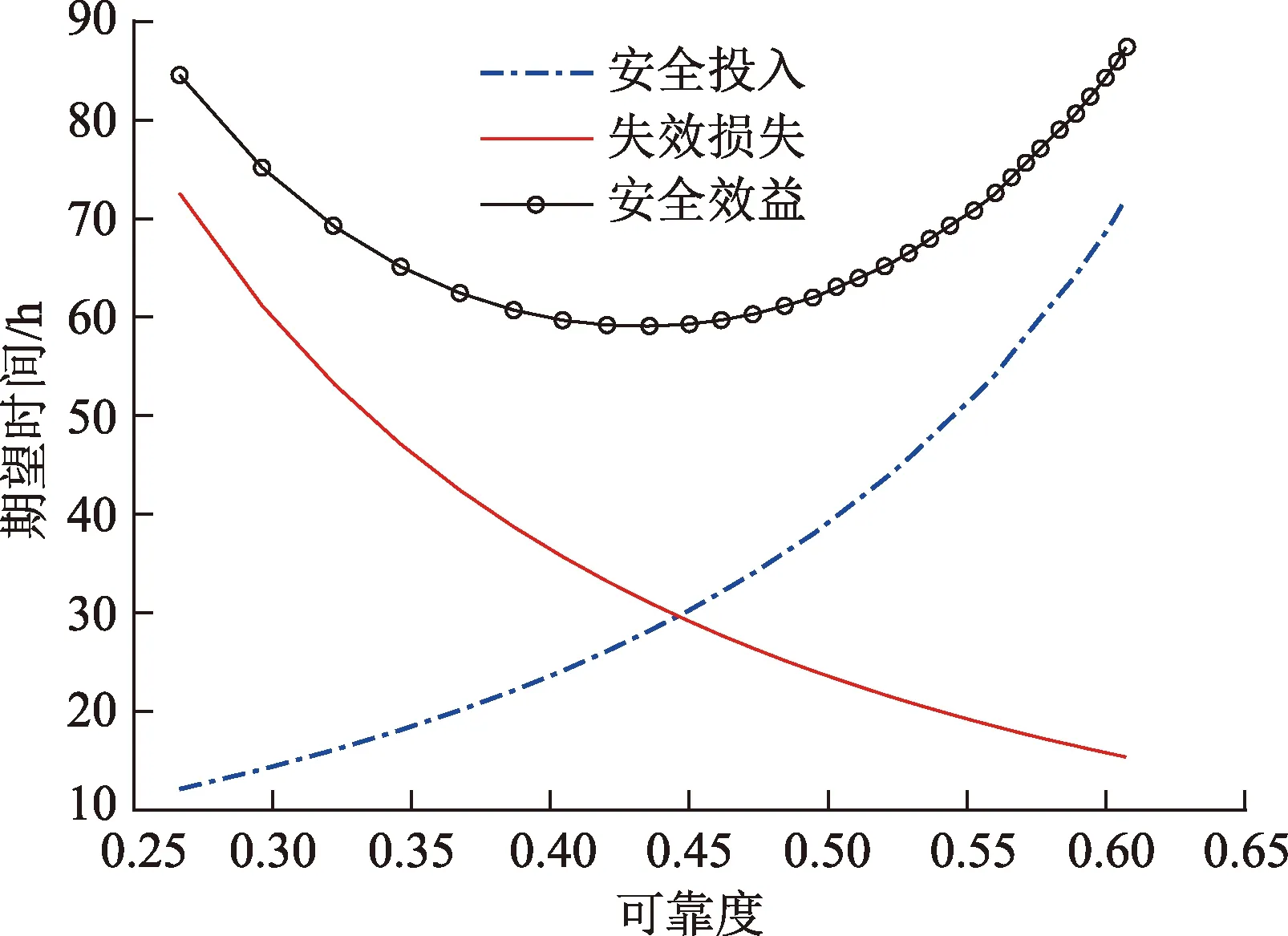
图7 隔水管下放试压安全效益曲线Fig.7 Safety benefit of pressure test in riser running

由图6可知:随着下放试压安全检测次数的增加,隔水管的下放试压作业有序进行,系统的风险熵逐渐降低;由式(5)可靠性指标与风险熵的映射关系,获得隔水管下放试压的整体可靠性逐渐增加。结合图7可知:增加试压次数在提高隔水管下放试压整体可靠性的同时,导致安全投入的时间成本逐渐提高,失效损失的时间成本逐渐下降;隔水管下放试压作业的安全效益曲线类似于开口向上的二次曲线,随着可靠度的增加呈现先减小后增加的趋势。所建模型综合考虑可靠性与期望时间的相互关系,有利于不同风险偏好的决策者进行选择。对于冒进型决策者愿牺牲一定的可靠度而追求较小的乐观作业时间,可选择安全效益曲线左侧节点相应的实施方案;对于保守型决策者不愿意承担因试压失败而付出的失效损失时间,可选择安全效益曲线右侧节点相应的实施方案;对于风险与效率均衡的于中间型的决策者可选择安全效益曲线最低点相应的实施方案。

4 试压方案的影响因素

4.1 密封可靠性

按照应用实例所示配置及基本参数将隔水管单根连接的密封可靠性作为单一变量,分析密封可靠性对安全效益曲线及最优试压次数及位置的影响,结果如图8与表3所示。

图8 不同密封可靠性下安全效益曲线Fig.8 Safety benefit under different sealing reliabilities

由图8可知:不同密封可靠性条件下深水钻井隔水管下放试压的安全效益曲线均近似于开口向上的二次曲线,安全效益时间随着可靠度增加先降低后增加,最低端的拐点位置即为风险与效率协调最优位置;随着单根密封可靠性增加,安全效益曲线向右下方移动,这是由于随着单根密封可靠性增加,隔水管系统下放试压的整体可靠度增加(向右移动),进而导致失效损失的时间成本降低(向下移动)。由此可见,从技术与装备的角度提高隔水管单根连接的密封可靠性,是提高隔水管下放试压过程安全性与作业时效性的根本途径。

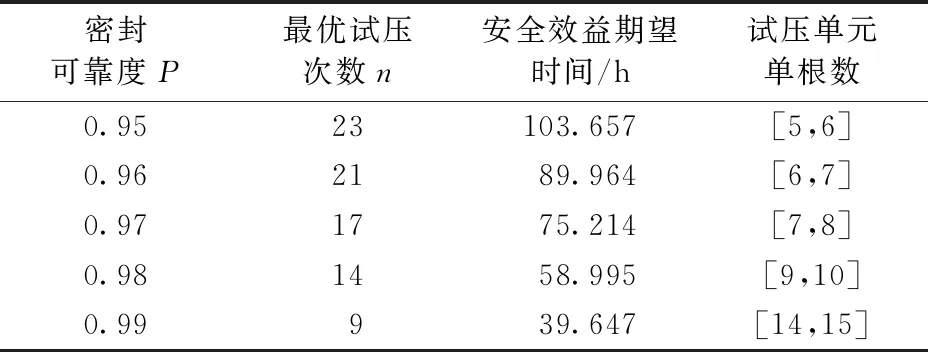
表3 不同密封可靠性下结果分析Table 3 Analysis results under different sealing reliabilities

分析表3可知:随着单根连接密封可靠性的增加,最优试压次数逐渐减少,说明作业者可依据密封可靠性的提高适当减少试压次数以提高作业效率;安全效益时间随着可靠性的增加而逐渐减少,并与图8中相应曲线的低部拐点对应;随着密封可靠性的增加,试压单元的最优单根数目逐渐增加,具体数据可为现场下放试压单元的设置提供参考。

4.2 井位水深影响

分别以1 000 m(43根)、1 500 m(65根)、2 000 m(87根)、2 500 m(109根)、3 000 m(131根)水深为例进行分析,研究不同井位水深对安全效益曲线及最优试压次数及位置的影响,结果如图9与表4所示。

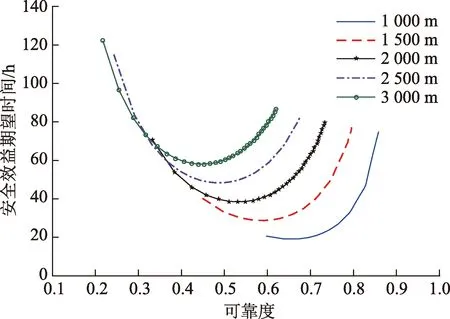
图9 不同水深下安全效益曲线Fig.9 Safety benefit under different water depths

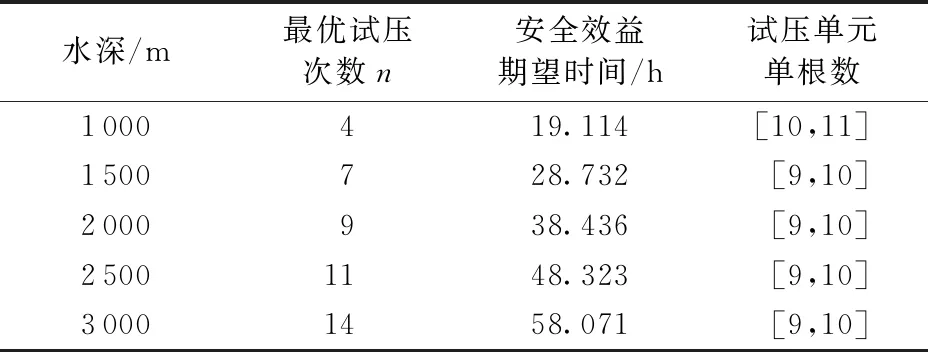
表4 不同水深下结果分析

由图9可知:不同井位水深条件下深水钻井隔水管下放试压的安全效益曲线同样为二次曲线形状,随着水深增加,隔水管系统下放试压的安全效益时间与可靠度的变化范围有所增加;随着作业水深(隔水管系统单根数目)增加,安全效益曲线向左上方移动,这是由于随着作业水深的增加,隔水管单根数目及连接次数增加,系统可靠度降低(向左移动),失效损失的时间成本增加(向上移动)。由此分析,对于深水井宜采用长度较大的隔水管单根,以减少隔水管单根数目及连接次数,提高隔水管系统下放试压的可靠性与高效性。

分析表4可知:随着水深增加,隔水管下放试压的最优次数与安全效益时间呈现线性增长的趋势,然而最优试压单元的根数基本不变。说明水深对于隔水管下放试压系统可靠度的影响较大,但对于试压单元单根数目的选取影响较小。

5 结 论

(1)钻井隔水管下放试压智能优化方法具有较好的全局搜索能力和探索能力;依据优化结果开展试压作业有望节约可观的钻井成本;隔水管下放试压安全效益曲线随可靠度增加呈现先减小后增加的趋势;所建模型考虑可靠性与期望时间的关系,有利于不同风险偏好的决策者进行选择。

(2)随着单根密封可靠性的增加,安全效益曲线向右下方移动,单根密封可靠性是确定试压单元单根数目的关键因素;随着作业水深的增加,安全效益曲线向左上方移动,隔水管下放试压的最优次数与安全效益时间呈现线性增长的趋势,但最优试压单元的单根数目基本不变。