基于IBM Q平台的量子图像算法研究
任凤娟, 滕奇志, 王正勇, 何小海, 周 磊
(四川大学电子信息学院, 成都 610065)
1 引 言
量子图像处理作为量子信息科学的一个重要分支,旨在结合量子计算的并行性[1]和纠缠性[2],实现量子加速,提高计算能力,减少计算资源,完成信息的安全传输,最终解决一些在经典计算机上无法解决的问题.量子图像处理技术的发展将为医学[3-4],军事及环境保护等方面做出巨大贡献.
过去的十年中,在量子图像处理技术领域的研究得到了一定的发展,如量子图像表达式的制备[5-7],量子图像的几何变换[8],量子图像加密[9]等.量子图像分割作为量子图像处理领域的一种重要处理方法,有时为了有效地识别和分析目标区域[10],往往需要将目标区域从整体区域中分割出来.而量子图像分割的主要方法之一便是阈值分割,阈值分割主要使用阈值将灰度图像转换为二值图像以实现分割.
2016年5月,IBM对外提供了开源的5比特量子云平台[11],用户可以在这个平台上使用真实的量子计算机进行量子操作,也可以使用IBM云平台连接至IBM的量子计算机进行体验.2017年12月,IBM再次宣布推出其首个具有20个量子比特的IBM Q Network客户端.近年来,基于IBM 量子计算机的研究已经越来越多,例如:自动纠错[12],计算汉明距离[13]和区分高度纠缠的Z-状态[14]等.然而,大多数基于IBM量子计算机的研究仅用于实现量子计算和量子物理算法,却很少用于量子图像处理技术的实现.量子图像处理的应用研究也处于起步阶段,大多数量子图像的研究仅涉及理论方面,或者在经典计算机上仿真实现,却很少在量子计算机上进行处理.
基于上述问题,本文提出了一种基于IBM量子实验平台(IBM quantum experiment platform, IBM Q)的量子图像处理方案.该方案主要包括4步:(1) 将经典图像转化为量子图像并由提出的改进型强化量子图像表达式(an improved enhanced quantum representation,IEQR)存储量子图像信息;(2) 构建量子图像分割电路,并根据IEQR表达式初始化量子电路;(3) 利用IBM 量子实验室提供的开源量子计算工具包Qiskit,以Python语言为框架,将设计的量子图像处理电路编译成量子编程语言QASM,分别在IBM Q和经典计算机仿真两种平台下,实现了量子计算机下的量子图像分割处理;(4) 根据坍塌后的IEQR表达式,将分割后的量子图像转换为经典图像用于显示.
IEQR表达式是对新型强化量子图像表达式[7](novel enhanced quantum representation,NEQR)的改进,NEQR通过颜色信息和位置信息的纠缠来存储图像.在很多情况下,量子图像处理电路不仅包括颜色信息和位置信息,往往还包括很多其他信息位,例如量子图像分割所需的阈值信息,辅助信息等.所以在针对量子图像处理时,NEQR模型不能很好的对所有量子位信息进行跟踪和描述.本文对NEQR进行了改进,使改进后的IEQR表达式不仅能存储颜色和位置信息,还能够存储量子图像处理电路所需的其他信息,可以实现对量子电路的所有量子信息位的跟踪查看.
对于一幅灰度级为2m的2n×2n大小的图像,它的NEQR表达式|I>为
|I>=|C>m⊗|P>2n=
(1)
其中,“⊗”是量子计算中的直积符号[15],是一种实现量子逻辑门操作的重要运算方式; |C>m是颜色信息位;|P>2n是位置信息位,下标数字代表需要多少个量子比特位来存储该信息位.f(x,y)代表图像(x,y)处的灰度值.但是针对量子图像分割电路,除了图像的颜色信息和位置信息,还有阈值信息|T>m,以及三种辅助信息:|Ae_q>2m、|C_q>1和|q>4,因此改进后的IEQR表达式|I0>为
|I0>=|Ae_q>2m⊗|T>m⊗|C>m⊗
|P>2n⊗|C_q>1⊗|q>4=
|Ae_q2mTmCmP2nC_q1q4>
(2)
其中,|Ae_q>2m是旋转二值信息位,用以设定分割后二值图像的两个灰度值,因此需要2m个量子比特位;|T>m是阈值信息,即设定的一个灰度值,因此需要m个量子比特位;|C_q>1是控制辅助位,它的值表明了图像灰度值与阈值的大小关系,只需要一个量子比特位;|q>4是辅助位,用于辅助构成电路,为冗余信息位.所以针对一幅灰度级为2m的2n×2n大小的图像分割,我们共需要4m+2n+5个量子比特位.
在IBM Q平台处理量子图像的第一步便是将经典图像转换为量子图像.由于IBM Q平台上量子计算机的量子比特位数量的限制,目前还无法对大尺寸的多灰度级图像进行处理,因此只能将传统的8比特图像的灰度级将为4来进行后续分割处理,这样就只需要两个量子比特位来存储灰度信息,很大程度上减少了量子比特位的消耗.降低灰度级的映射关系如下.
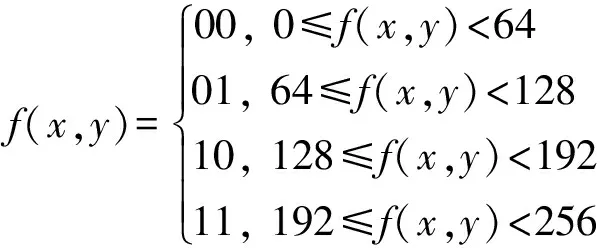
(3)
为了更好的阐述IEQR表达式,图1给出了一幅2×2大小的图像,下文的所有操作也将基于图1所示图像进行举例说明.
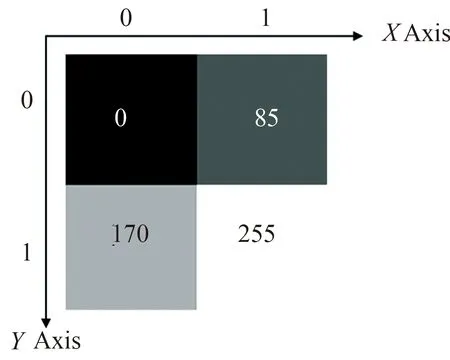
图1 一幅2×2大小样例图像Fig.1 A 2×2 example image
图1中的“XAxis”和 “YAxis”分别表示了图像的x和y坐标位置,灰度值在图像上标出.本文不考虑如何选取阈值,直接将阈值设定为|10>,其他阈值设定会在仿真实验分析处给出介绍;分割后的二值图像的两个值分别为|11>与|00>,所以旋转二值信息位|Ae_q>2m的值为|1 100>.所以图1 的IEQR表达式为
|85>⊗|01>+|170>⊗|10>+|255>⊗
|11>)⊗|C_q>⊗|q>=
|10>|10>+|11>|11>)|0>|0000>=
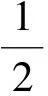
|110010101000000>+|110010111100000>)
(4)
3 量子图像分割电路
图2所示为量子阈值分割电路[16]的整体结构图,每个量子位的名称和初始化值都在图的左侧标出.该电路主要是由量子图像信息的输入、灰度值与阈值的比较,颜色信息与相应旋转二值信息位的交换三部分构成.
在第一部分,量子图像信息的输入时,由于量子系统的初始状态都是|0>,所以需要根据IEQR表达式对电路的各个量子位进行初始化.对于阈值信息和辅助信息等一些确定的量子位,本文使用一种通用的初始化方法,如果IEQR序列的状态为|1>,就直接将NOT门应用到相应的状态位,如果状态为|0>,则不做任何处理.但是对于颜色和位置信息,往往不采用通用的初始化方法.量子图像的位置和灰度信息是通过两个纠缠的量子序列的叠加态来存储整幅图像,根据文献[5]所述,需要找出灰度信息与位置信息之间的关系,然后利用H门(Hadamard)、NOT门和控制非门(Control-NOT,C-NOT)门的组合来初始化.图1的颜色和位置信息初始化如图3所示.q[2]和q[3]表示颜色信息,q[0]和q[1]表示位置信息.通过位置信息上的H变换,得到完全覆盖图像所有位置的叠加状态, 然后运用C-NOT门操作可以实现颜色序列和位置序列的纠缠,如图3(b)所示.
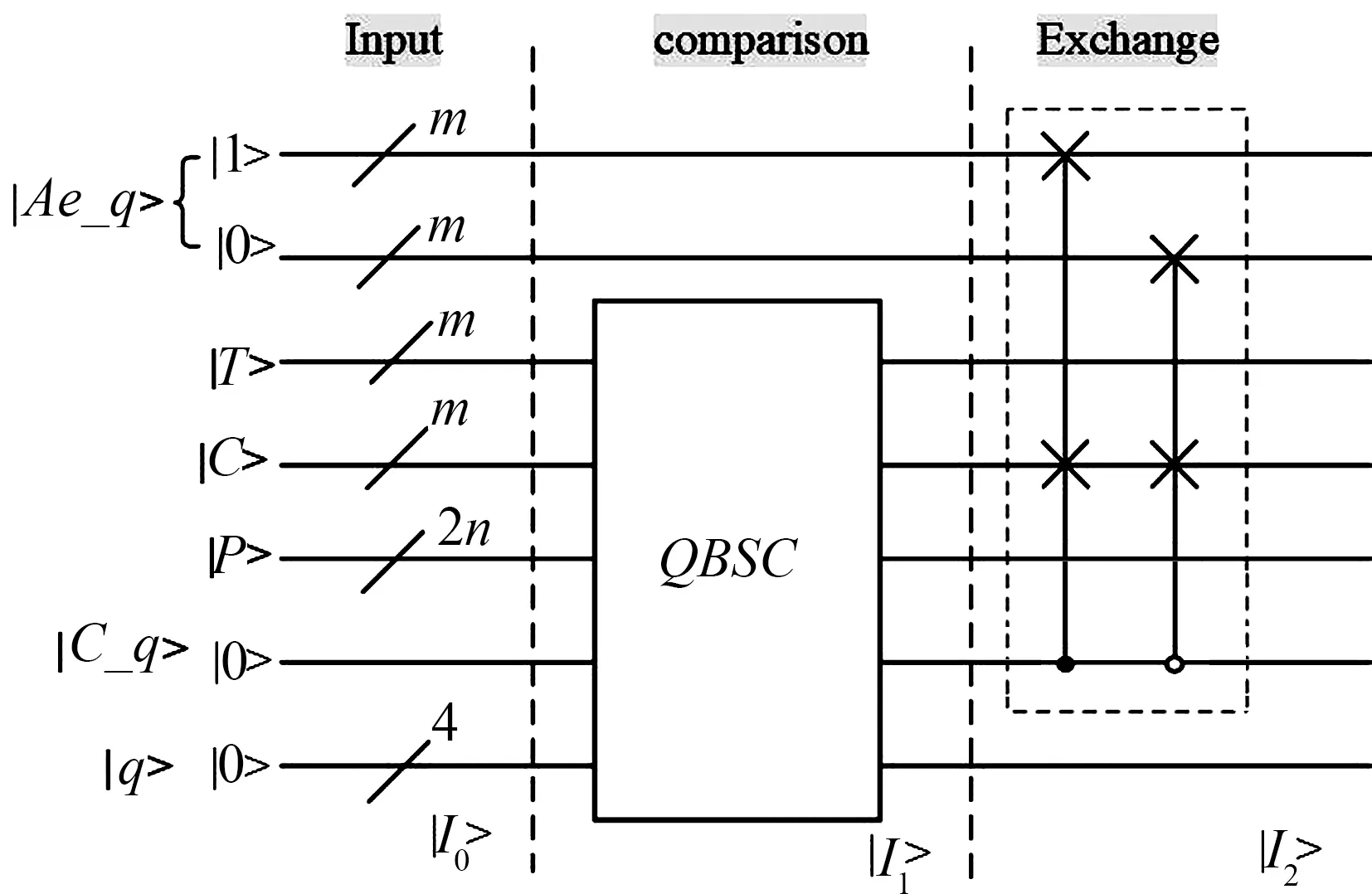
图2 量子阈值分割电路结构图Fig.2 Quantum threshold segmentation circuit structure

(a)颜色和位置初始化电路

(b) 坍塌结果图
Fig.3 Color and position information circuit initialization
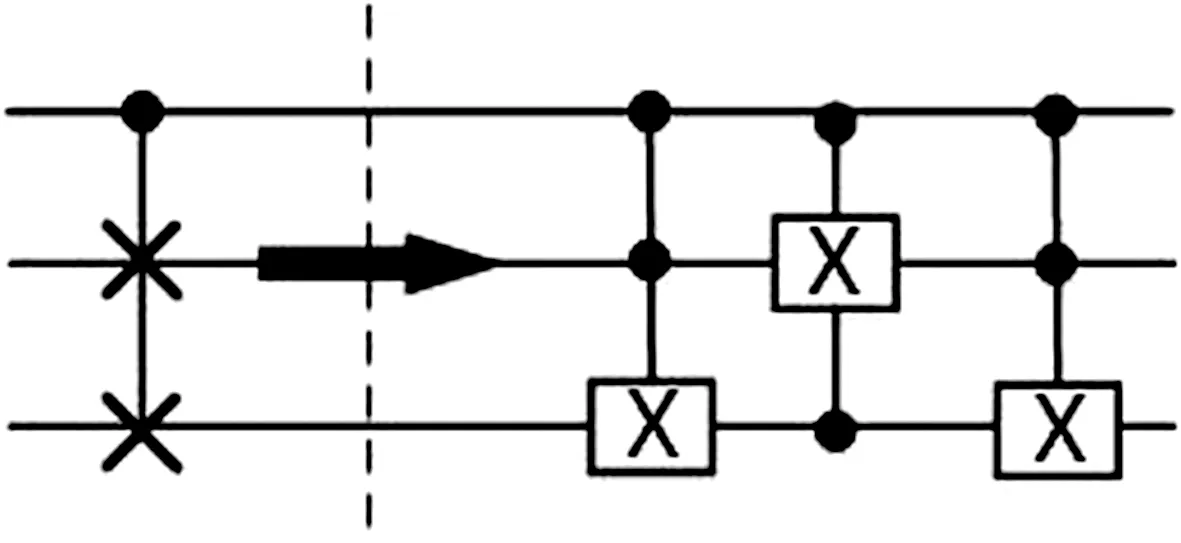
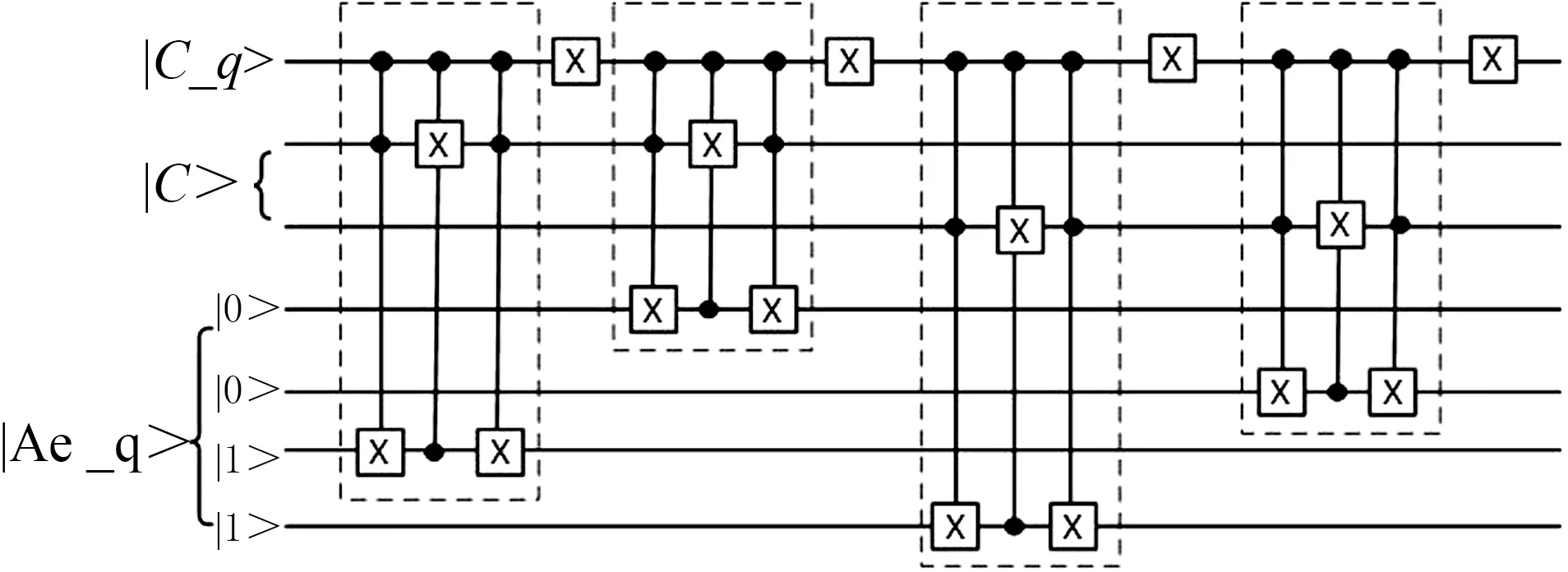
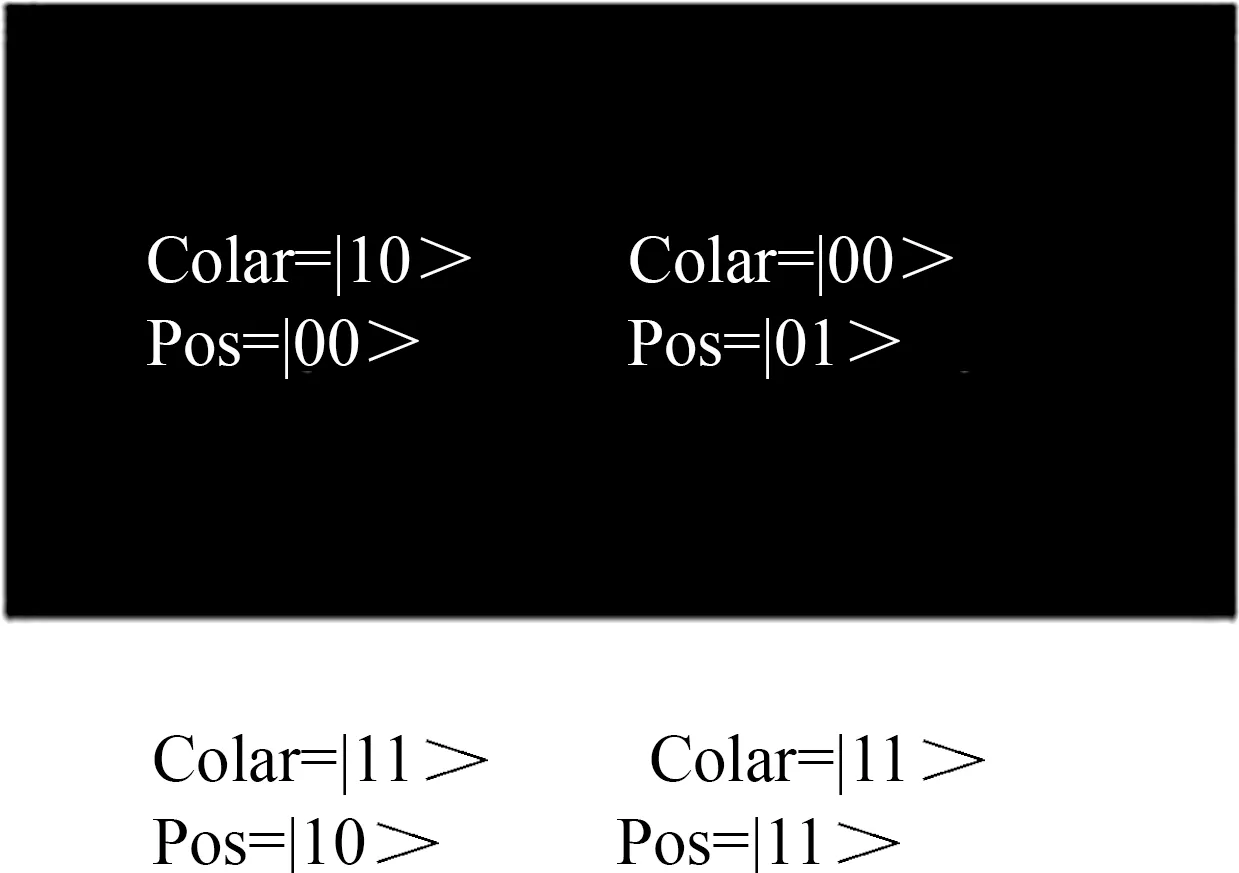
灰度值与阈值的比较则通过量子比特串比较器[17](quantum bit string comparator, QBSC)来实现,图4(b)是QBSC电路图,它是由两个UCMP构成的. |a>和|b>作为UCMP的输入, |x>和|y>作为UCMP的输出:当a>b时,x=1,y=0; 当a (a) 一量子位比较电路UCMP (b) 基于UCMP的两量子位比较电路图4 基于UCMP的量子比特串比较器电路Fig.4 Quantum bit string comparator circuit based on UCMP 当颜色与阈值比较过后,图像的IEQR表达式将由|I0>变为|I1>,|I1>表示如下. |110010010100010>+|110010101010001>+ |110010111110011>) (5) 从中|I1>也可以看出|C_q>的状态发生了变化.当|C_q>=|1>时,即C≥T时,颜色信息|C>m将与旋转二值信息|Ae_q>2m的高m位发生交换,当|C_q>=|0>时,即C (a) Cswap等效电路 (b) 基于Cswap等效电路的交换电路图5 颜色值与旋转二值信息交换电路Fig.5 Color information and rotation information exchange circuit 当颜色值与旋转二值信息|Ae_q>2m交换过后,即完成了量子图像的分割,图像的IEQR表达式将由|I1>变为|I2>,|I2>是经过量子阈值分割后的通过量子测量获得的坍塌量子序列,它的IEQR表示如式(6)所示,从式(6)中可以看出颜色值与旋转二值信息的相应量子位已经发生了交换. |110110000100010>+|100010111010001>+ |110010111110011>) (6) IEQR将量子图像的颜色信息、位置信息和一系列其他信息均存储在量子序列的叠加状态中.通过对量子位的测量操作,量子序列会发生坍塌,以概率幅度的形式输出,最后将位置信息及其对应的颜色信息从坍塌的量子序列中提取出来.在量子图像阈值分割之后, 颜色信息只会是|Ae_q>2m中预先设定的值:|11>或|00>.提取出的颜色和位置信息仍然是量子序列,为了在经典计算机上显示分割后的量子图像,需要将量子序列转换为经典数字图像状态.应用式(7)对颜色信息进行转换,位置信息量子序列的转换直接将二进制转换为十进制对应坐标.例如,坍塌后量子序列是|100010111010001>,则其颜色信息是|11>,通过式(7)映射为255,其位置信息是|10>,其对应于x坐标位置为1且y坐标为0.因此,在一个空白图像中,像素坐标(1,0)的灰度值可以设置为255.以此类推,绘制整个图像. (7) 图1所示2×2的图像经过阈值为|10>的量子电路分割后的量子图像转换为经典图像后如图6所示.每个像素块中的“color”表示灰度值,“Pos”表示像素块的位置坐标. 图6 分割后输出图像Fig.6 Output image after segmentation IBM量子实验室为研究人员提供了两种运行量子算法的工具:IBM Q Experience和经典计算机模拟器.IBM Q Experience是一个将量子计算机放在云上的平台, 研究人员可以使用IBM Q Experience在真实量子芯片上执行自己的量子算法,通过编写量子编程语言QASM或操作门电路来实现自己的算法.经典计算机模拟器是在经典计算机上利用IBM量子实验室提供的开源量子计算工具包qiskit,以python语言为前端接口来编写实现自己的量子算法,并在经典计算机上仿真实现量子算法. 基于第3节的量子图像阈值分割电路,本文分别在IBM Q Experience和经典计算机模拟器中进行了不同次数的迭代实验.图7给出了在两种运行环境下128次迭代测量的结果.从图7可看出,坍塌后的量子序列保持一致,颜色信息(每个量子序列中的第7位和第8位)仅呈现出|00>与|11>两种状态.而坍塌后量子序列的概率幅度不一样,这也验证了量子系统的随机性与“测不准”原理. (a)IBM Q Experience (b) 经典计算机仿真 Fig.7 The results were measured 128 times on differernt platforms 另外,我们统计了在不同运行环境下不同迭代次数的运行时间,如表1所示.表1的第一行是迭代次数,第二行和第三行是在相应迭代次数下在不同运行环境中操作的时间. 使用经典计算机模拟时,Python语言的时间函数可以准确计算实现分割所需的时间. 但是,对于IBM Q Experience,只有基本的逻辑门操作,并且不存在其他辅助函数功能,因此我们只能手动测量运行时间,为了提高数据的可靠性,本文在一个迭代次数下手动测量10次并记录10次测量的一个时间范围. 表1 在不同环境下的运行时间 从表1可以看出,IBM Q Experience的运行时间明显少于经典计算机模拟的运行时间. 经典计算机上的运行时间随着迭代次数的增加呈指数级增长,当迭代次数为1 024次时,总花费为6 702.91 s,相当于约2 h;而量子算法在IBM Q Experience上运行时,运行时间非常短,花费的时间在2~4 s的范围内. IBM Q Experience允许最大迭代次数为8 192次. 本文也在8 192次迭代下也运行分割算法,时间花费仍只需要3~4 s.实验结果证明了量子计算机计算能力的优越性. 根据第4节中的内容,本文对坍塌后量子序列进行后处理以实现量子序列的可视化.图8显示了两组2×2大小量子图像经过不同阈值的量子图像分割运算后的结果. 同时,我们还对4×4大小图像在IBM量子实验平台上实现了量子阈值分割操作.分割结果如图9所示.当迭代次数为32次时, 4×4大小量子图像阈值分割在经典计算机模拟中花费了963.81 s时间,相对于表1所示2×2大小量子图像在32次迭代情况下所花费的208 s时间,说明了在经典计算机实现量子算法的模拟过程,随着量子位数的增加,时间花费也将大量增加. 理论上,随着量子算法的量子比特数量的增加,经典计算机仿真所需内存和时间花费将呈指数增长.因此在经典的计算机模拟环境下,限制大规模量子图像处理存在两个主要问题:一个是内存,另一个是时间花费.虽然经典计算机下的仿真实验受到诸多因素的限制,不能轻易完成量子图像算法的研究工作.但本文将低量子比特量子图像算法在IBM Q平台上得到充分论证,为量子图像研究的进一步发展提供了新的方向.目前,IBM量子实验室已提供高达30位的量子云模拟器.与经典计算机环境下的仿真过程相比,它具有更短的时间和更快的速度.然而,由于商业化的局限性和许多其他因素,无法在云模拟器上模拟更大规模量子图像处理算法. 基于NEQR量子图像表达式,提出了IEQR量子图像表达式.通过可编程量子计算机和量子编程语言实现了从经典数字图像到量子图像的转换,在IBM Q平台上实现了2×2和4×4大小量子图像在不同阈值下的图像分割,证明了在IBM Q平台上处理量子图像算法的可行性,也验证了阈值分割电路的正确性.最后用概率图的形式证明了在IBM Q Experience和经典计算机模拟器两种实验平台下结果的一致性,同时给出了两种平台下不同迭代次数的运行时间,验证了量子计算机计算能力的优越性.本文在IBM Q上实现了量子图像的阈值分割,为IBM量子实验平台中更多的量子图像处理奠定了基础.未来的工作将集中在如何使用量子纠缠理论来加速量子图像处理的过程以及如何在量子图像中实现多目标检索功能.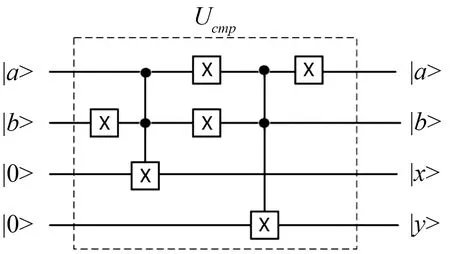

4 分割后量子图像的显示

5 IBM Q仿真实验及分析
5.1 坍塌后的量子序列
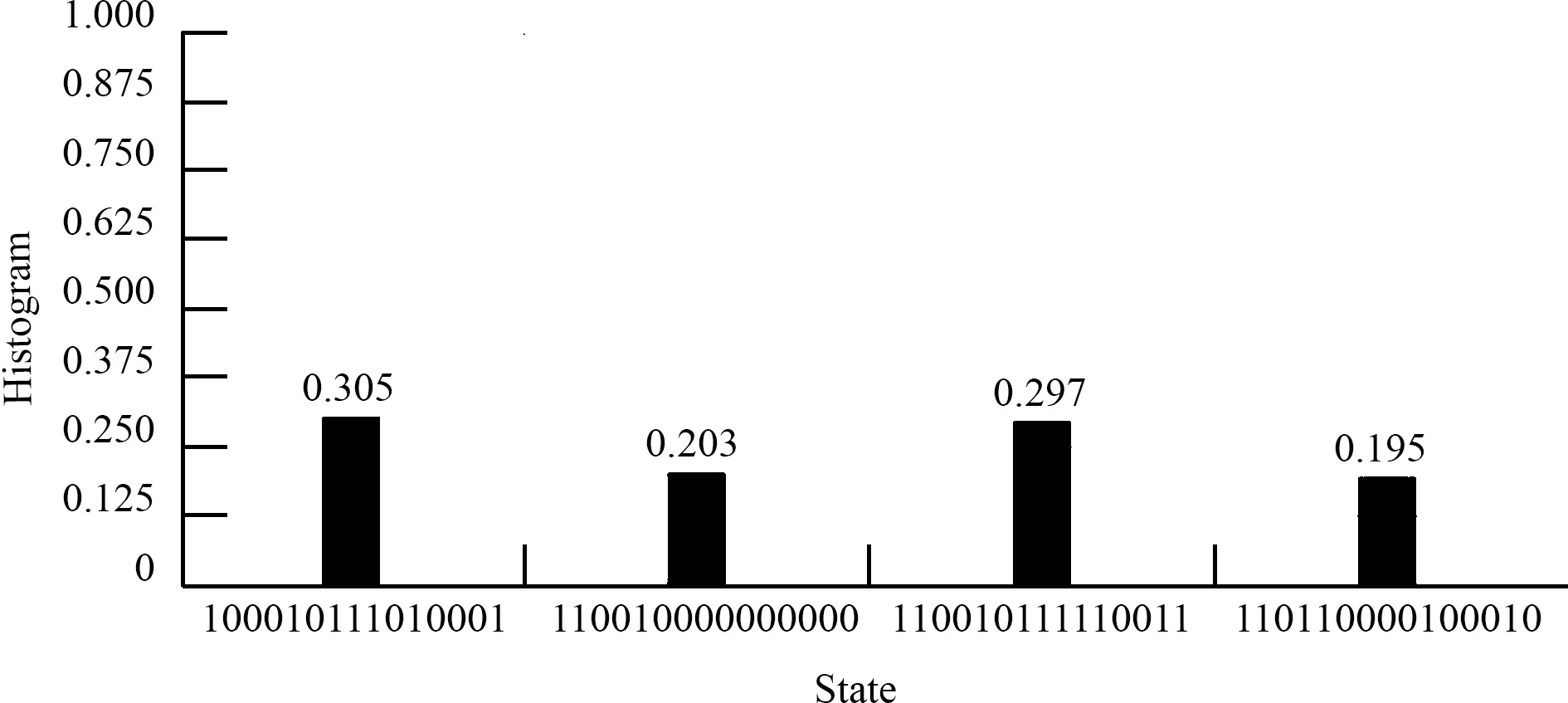
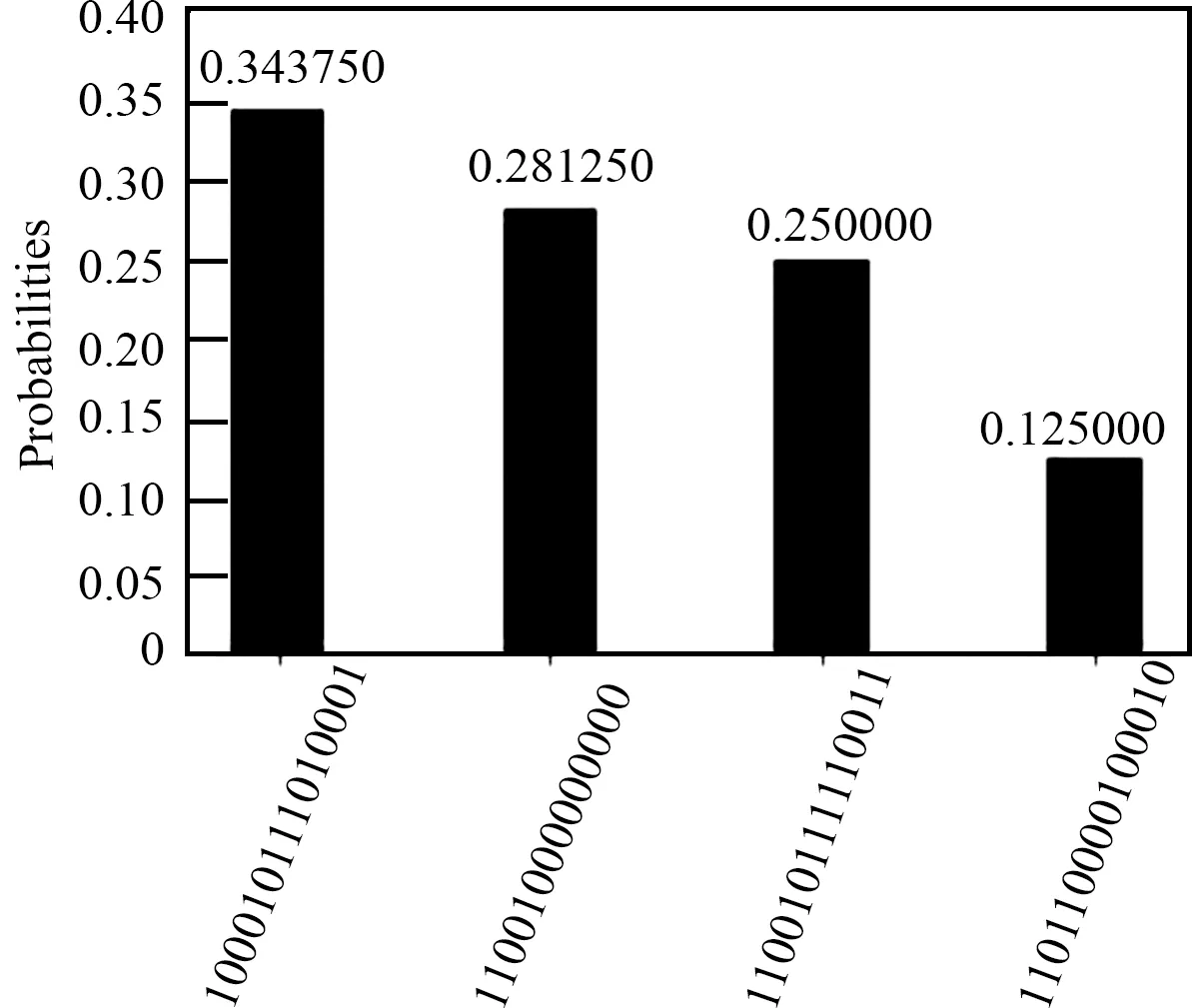
5.2 运行时间比较

5.3 量子阈值分割结果图

6 结 论

