类脑计算的基础元件：从忆阻元到分忆抗元

蒲亦非， 余 波， 袁 晓

(1.四川大学计算机学院， 成都 610065； 2.成都师范学院物理与工程技术学院， 成都 611130； 3.四川大学电子信息学院， 成都 610065)

1 引 言

根据电路基本变量组合完备性原理，1971年美籍华裔科学家蔡少棠先生从理论预测出忆阻元(Memristor)的存在性，称忆阻元为人类迷失的第4种基本电路元件，并得到学界的广泛认可[1-3].忆阻元的记忆可以是非易失的，也可以是易失的；忆阻元可以是无源元件，也可以是有源元件；忆阻元可以是动态元件，也可以是非动态元件[3-6].蔡先生还依据电路变量与电路元件的公理完备性、逻辑相容性和形式对称性等，提出公理化的电路元件体系——蔡氏公理化元件系，进而得到电路元件的蔡氏周期表[1-3,7-10].值得注意的是，根据蔡氏公理化元件系的理论，一种基本电路元件(例如电阻元、电容元、电感元、忆阻元等)是不可能由其他各种基本电路元件通过串并联等无源方式来实现的，但可能由其他各种基本电路元件通过有源方式来实现(例如用电容元通过有源元件来实现电感元)；而一种电路器件(例如积分器、微分器、对数与反对数放大器、电压-电流变换器、比较器等)是可以由各种基本电路元件通过某种方式来实现的.从这个意义上讲，有学者将memristor翻译为忆阻器是不恰当的，忆阻元是一种基本电路元件，而非一种电路器件.为了强调电路与系统这一基本理论，本文建议对电阻元、电容元、电感元、忆阻元、分抗元(分数阶电阻元)、分忆抗元(分数阶忆阻元)等基本电路元件采用“元”，而非采用“器”来对其进行标识.在实际使用中，为了标识简便，可以省略后面的“元”字.

2008年，Nature报道了美国科学家Williams领导的团队在纳米尺度下制造出的忆阻元物理实体[11]，震惊国际电工电子领域，在全世界范围内掀起了对忆阻元的研究热潮[12-17].单个忆阻元即可模拟突触的基本功能，实现突触的可塑性，忆阻元已逐渐成为实现类脑计算系统的基础元件[14-15].忆阻元能同时完成存储与计算功能，成为未来信息存储与计算融合的非冯·诺依曼计算体系的关键元件，在计算机科学、神经网络、生物工程、通信工程和非线性电路等领域有着广泛的应用前景[13].2008年，忆容元和忆感元的概念也被提出，并得到人们的关注和研究[16-17].

分数阶微积分已成为数学分析的一个重要分支[18-19].由于分数阶微积分具有长时记忆、非局部性和弱奇异性的特点，物理科学家和工程技术人员将其作为一种新的数学方法[18-19].在许多科学领域，如分数扩散过程、分数阶粘弹力学、分形动力系统、分数阶控制、分数阶图像处理、分数阶信号处理、分数阶神经网络和分数阶电路与系统等，使用分数阶微积分已取得一些可喜成果[6,10,18-24].分数阶系统被称为21世纪的系统[24].把分数阶微积分应用到忆阻元的研究，还是一个新兴课题[25-35].基于忆阻元和分数阶微积分，用普通的忆阻元和电阻元、电容元等元件以模拟电路的形式实现分数阶忆阻元电路——分忆抗元电路，是一项有趣且很有挑战性的研究工作[34-35].

如何将分数阶微积分应用于现代信号分析与处理之中，目前在国际上是一个研究甚少的新兴学科分支.我们团队长期以来始终致力于分数阶微积分在信号处理、图像处理、电路与系统和机器智能中应用这一新兴学科分支的相关研究[6,10,23,34-46].受蔡氏公理化元件系启发，依据分数阶微积分理论，团队于2016年在国际上首次提出关于“分忆抗元(分数阶忆阻元)”的概念及其一般电气特性，创造了两个相应的新专业英文单词fracmemristor(分忆抗元)和fracmemristance(分忆抗值)[34]；并于2017年尝试用标度分形格型结构以模拟电路形式实现了国际上第一个分忆抗元，提出了鉴别分忆抗元的指纹特征，分析了分忆抗元和蔡少棠先生提出的经典忆阻元之间电气特性的相互转化关系，论证了经典忆阻元其实是零阶分忆抗元(经典忆阻元是分忆抗元的一个特例)[35].

2 记忆元件

荷控忆阻元的忆阻值受到电荷量控制，磁控忆阻元的忆阻值受到磁通量控制；荷控忆容元的忆容值记忆电荷量，磁控忆容元的忆容值记忆磁通量；荷控忆感元的忆感值记忆电荷量，磁控忆感元的忆感值记忆磁通量.分忆抗元是一个关于介于忆阻元和电容元或电导元之间的内插特性是什么，以及关于分忆抗在蔡氏电路周期表[10]中的位置在哪里的有趣问题.分忆抗元是分数阶忆阻元的一个合成词，可简称为分忆抗[34-35].分忆抗值是分忆抗元的分数阶阻抗值[34-35].表1清晰地展示了非记忆元件和记忆元件的名称、数学描述和符号或结构等信息.

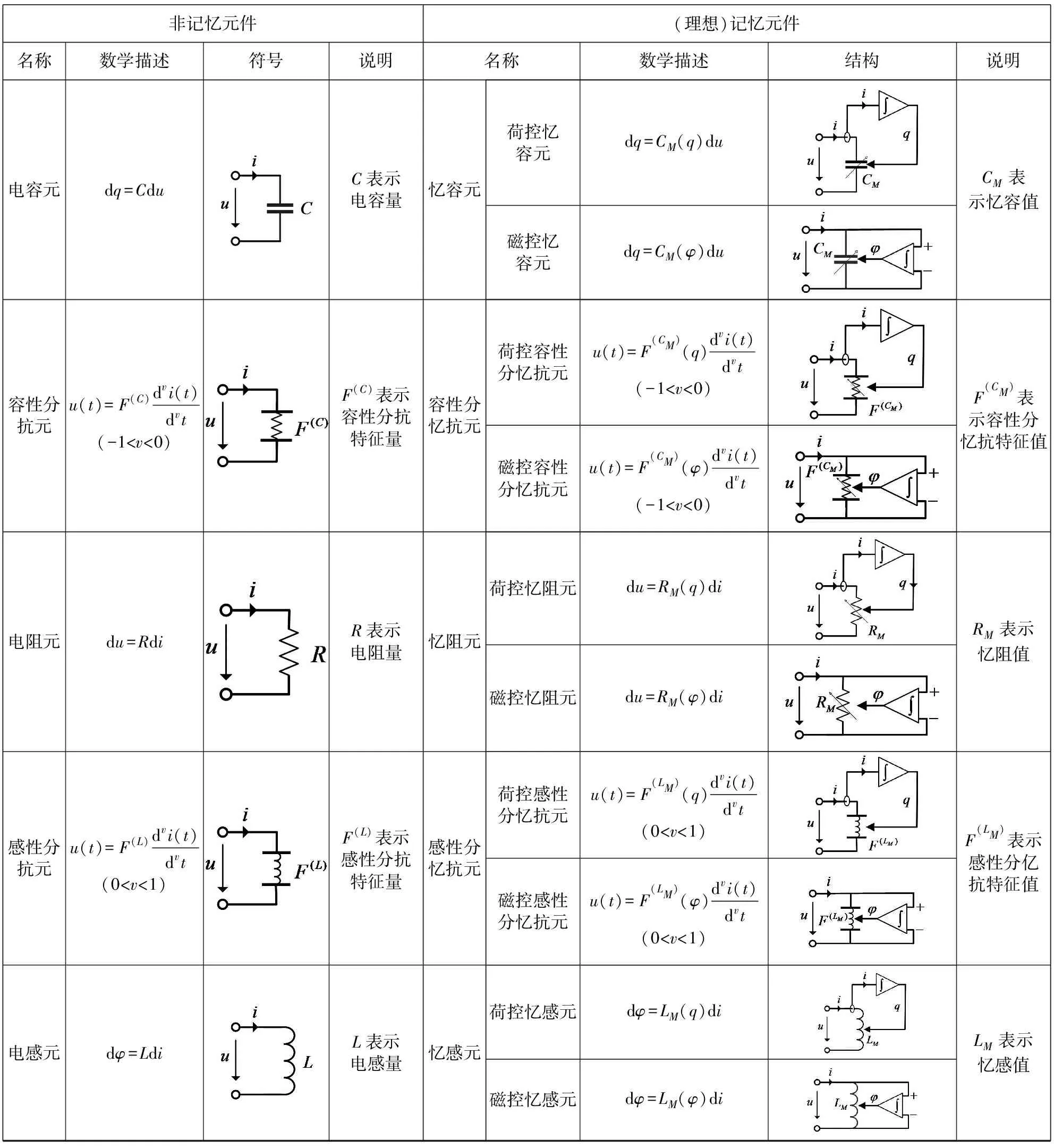
表1 非记忆元件和(理想)记忆元件的基本信息表

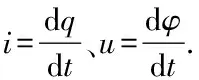
从系统的观点，一个系统的输出仅仅取决于该时刻的输入，这个系统就称为无记忆系统.如果是把电流输入到电容元，电容元二端电压作为输出，则电容元两端电压不仅与当前时刻的电流有关，还和过去的电流有关，称电容元是连续时间记忆元件.由于忆阻元、忆容元、忆感元和分忆抗元记忆了电荷量(电荷量取决于过去一段时间电流值的积分)和磁通量(磁通量取决于过去一段时间电压值的积分)，则称它们为记忆元件.电容元的记忆属于易失记忆，忆阻元、忆容元、忆感元和分忆抗元的记忆可以为非易失记忆.

忆阻元在双极性正弦信号激励下，其伏安特性曲线为捏滞回线[12-13].捏滞回线夹断面积随正弦信号频率增大减小，正弦信号频率趋于无穷大时捏滞回线收缩为一条直线.忆容的库伏特性曲线、忆感的韦安特性曲线也可呈现出与忆阻元的伏安特性曲线一样的捏滞回线特性[17].捏滞回线已成为判断一个元件是否为记忆元件的重要依据.分忆抗元的伏安特性呈现出与已有忆阻元、忆容元和忆感元不一样的指纹特征[34-35].

3 分数阶忆阻元的模拟电路实现——任意阶格型分忆抗元电路

依据分数阶微积分理论，电容元的运算阶为-1，电阻元的运算阶为0，电感元的运算阶为+1[10].运算阶介于电阻元和电容元之间的元件称为容性分抗元，运算阶介于电阻元和电感元之间的元件称为感性分抗元[10].目前还没有可商用的分抗元，人们提出各种各样的分抗逼近电路来近似实现分抗元的运算性能[6,10,41-43].从物理上来说，就是利用可实现的无源二端电路网络(特别是RC网络)来逼近理想分抗元的运算性能；从数学上来说，就是构造有理的阻抗函数序列逼近无理的理想分数阶微积分算子[44].分抗逼近电路是实现分忆抗元电路的基础.v阶容性格型分忆抗元电路由无限节次的格形电路级连而成，如图1所示[35].

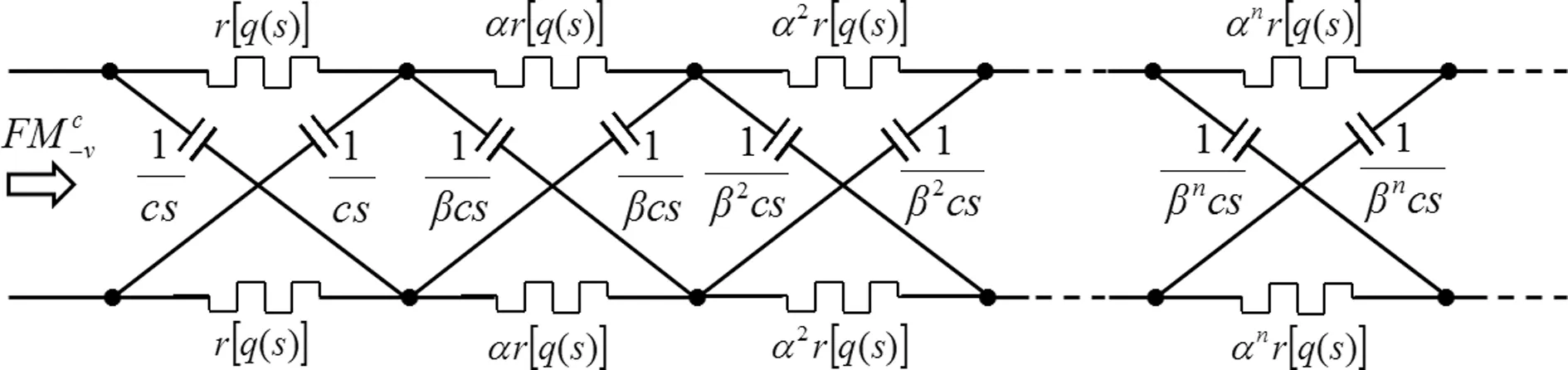
(a) ν阶低通容性格型分忆抗元电路

(a)ν-order low-pass filtering capacitive lattice scaling fracmemristor

(b) ν阶高通容性格型分忆抗元电路

(b)ν-order high-pass filtering capacitive lattice scaling fracmemristor

图1ν阶容性格型分忆抗元电路

Fig 1. Circuit configurations ofν-order capacitive lattice scaling fracmemristor

(1)

方程(1)表明，图1所示ν阶低通容性格型分忆抗元的分数阶阶次，本质上取决于它的两个正比例因子(α和β).特别是，若图1的两个正比例因子α=1和β=1，则为1/2阶容性格形分忆抗元.其逼近的阻抗函数为[35]

c-1/2{r[q(s)]}1/2s-1/2(α=1,β=1)

(2)

方程(2)表明，1/2阶容性格型分忆抗元是v阶理想容性分忆抗元的一种特殊情况.

4 任意阶分忆抗元具有的电气特性

鉴别一个电路是否为分忆抗元电路，应知道分忆抗元具有的电气特性，特别是其伏安特性曲线中具有的指纹特征.一般以电流控制式容性分忆抗元作为研究对象.假设输入到忆阻元和分忆抗元是相同的电流Ii(t)=sin(at)u(t)，其中a为电流源频率、u(t)为阶跃函数，即可得到分忆抗元的伏安特性曲线(理论计算过程略)如图2所示[35].从图2可知，如果理想容性分抗元和输入的双极性正弦信号的初值条件均为0，当阶次ν趋近于0时，容性分忆抗元具有和理想忆阻元一样的电气特性[35].

(1) 图2(a)的伏安特性中0.001阶容性分忆抗元的伏安特性曲线和理想忆阻元的伏安特性曲线基本重合，均过(0，0)点为捏滞回线.

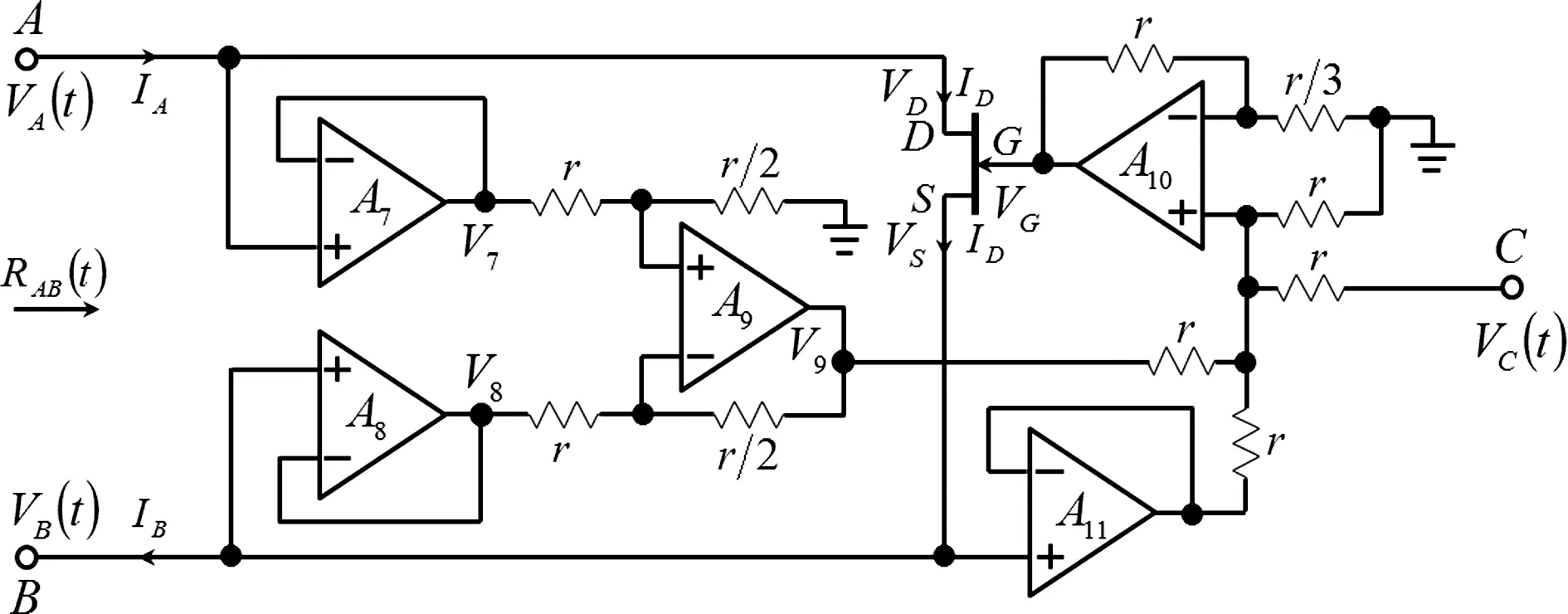
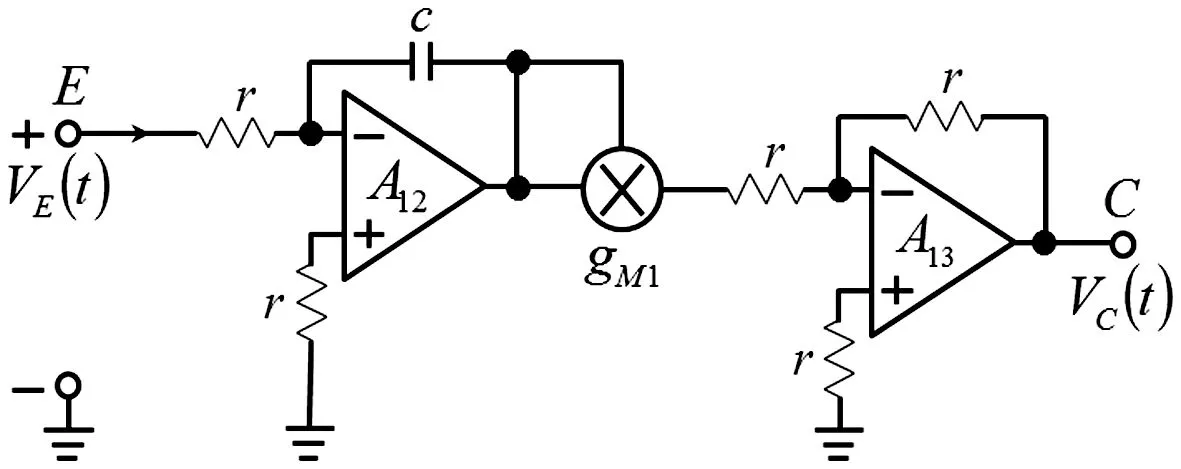
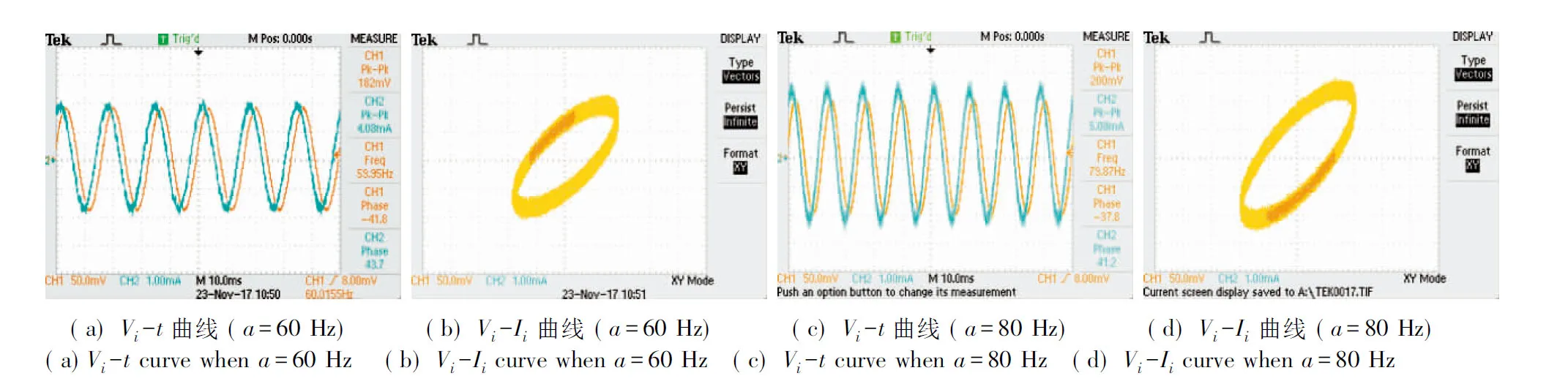
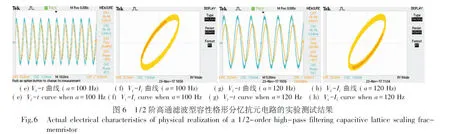
(2) 当容性分忆抗元的阶次v>0时，其电气特性介于电容元和忆阻元之间.特别是当0

(3) 当阶次ν为正整数时，理想容性分忆抗元内部具有整数阶积分特性，从图2(f)、 (j)和 (l)可知，其伏安特性曲线呈现出从(0，0)点开始的单圈扭曲的椭圆形状.

为得到输入电流Ii(t)的频率a对分忆抗元电气特性的影响.保持前面的分析参数不变，得到频率a=2 rad/s、a=3 rad/s、a=4 rad/s和a=100 rad/s时2/3阶理想容性分忆抗元的电气特性曲线如图3所示[35].

从图2(e)和图3知，理想容性分忆抗元在输入电流Ii(t)时，其二端电压Vi(t)包含许多谐波成分，谐波成分的大小和分布与分忆抗元的阶次ν、初值状态，以及电流的幅度和频率等有关.分忆抗元的响应为非线性的周期响应.从图3(a)、 (c)、(e)和(g)知，Vi-t曲线的幅度随着输入电流Ii(t)频率a的增大而减小.从图3 (b)、(d)、(f)和 (h)知，伏安曲线环路椭圆面积随着Ii(t)频率a的增大而减小.特别的，当a→时，伏安曲线由捏滞回线开始呈现出单值函数曲线.

综上所述，可将分忆抗元的指纹特征总结为4点[35].

(1) 如果理想容性分忆抗元的初始条件为0，且输入端双极性电流信号的初值为0，且阶次v趋近于0时，其所呈现的捏滞回线特性和忆阻元相同.

(2) 当0<ν<νth时，理想容性分忆抗元的伏安特性呈现出从(0，0)点开始的捏滞回线，然而各周期伏安特性曲线的交点不再固定到(0，0)点，其交点随着ν的变化而变化.当ν≥νth，且为非整数时，理想容性分忆抗元的伏安特性曲线不再具有捏滞回线，而是呈现出从(0，0)点开始的多种多圈扭曲的椭圆形状.

(3) 当阶次ν为正整数时，理想容性分忆抗元的伏安特性曲线呈现出从(0，0)点开始的单圈扭曲的椭圆形状.

(4) 理想容性分忆抗元伏安曲线的捏滞回线面积随信号频率的增大而减小，当信号频率很大时，伏安曲线由捏滞回线开始呈现出单值函数曲线.

5 实验测试

为完成1/2阶高通滤波型容性格形分忆抗电路设计，设计了一种压控浮地JFET忆阻元等效电路作为忆阻元电路如图4所示[35]，具体包括基于JFET的浮地压控线性电阻电路和电压控制源电路，电压控制源的输入端VE(t)取自于图1所示分忆抗元电路的输入端，电压控制源的输出端VC(t)的输出端连接到图4(a)所示电路的控制端VC(t).将图4所示电路取代图1所示电路中的忆阻元，即构成分忆抗元电路，实验测试照片如图5所示，实验测试结果如图6所示[35].实验测试结果与上述分忆抗元的电气特性分析结果相符.

(a)基于JFET的浮地压控线性电阻电路

(a) A floating voltage-controlled linear resistor achieved by JFET

(b)电压控制源VC(t)

(a) Vi-t曲线

(b) Vi-Ii曲线

Fig.5 Physical realization of a 1/2-order high-pass filtering capacitive lattice scaling fracmemristor

6 结 论

分忆抗元的电气特性与输入电流的历史有关，并能实现分数阶微积分运算.本文在介绍忆阻元、忆容元、忆感元和分忆抗元等概念的基础上，给出一种关于任意阶分忆抗元的模拟电路实现形式，分析分忆抗元应具有的电气特性，实验结果印证了理论分析的正确性.参考本文的方法，结合分抗逼近电路的原理，还有很多种任意阶分忆抗元电路实现方式可开展，比如任意阶树枝型分忆抗元、任意阶网格型分忆抗元、任意阶两回路型分忆抗元和任意阶H型分忆抗元电路等.分忆抗元的概念是对经典忆阻元概念的延伸，目前分忆抗元主要在物理和数学方面研究.关于分忆抗元的其它电路实现、在类脑计算中的应用，还有很多需要进一步深入研究的挑战性问题.