基于“双控”维修模式的装备维修计划制定方法

周成杰，蒋铁军

(海军工程大学， 武汉 430000)

随着越来越多的高新技术被应用在装备领域，装备更新换代的速度明显加快，高新技术的应用一方面能够提升装备效能，另一方面会增加维修难度和维修成本，进而导致维修经费的提高。当前装备维修计划的制定基本上以经验为主，大多靠人工进行编制，没有站在全系统全寿命的角度，缺乏科学的理论方法指导。在维修经费有限的情况下，如何制定科学的装备维修计划，发挥装备维修费的效益，保证装备效能的最大化，是当前面临的一个重大问题。

目前，大型装备大多采用“定期+双控”的维修模式，修理时间按照预先确定的修理间隔实施装备的各等级修理，修理价格实行计划和经费的“双控”管理模式，即舰船等级修理经费按照计划价格进行决算。这种维修模式的好处在于能做到对维修工期和维修经费的掌控，使装备在一个适度的范围内进行维修，比较符合维修实际。

针对维修计划的制定，黄傲林等[1]以长期运行费用率为评估指标,研究了劣化系统的周期预防性维修策略；付芳[2]研究了基于可靠性的机电设备维修计划优化；李有堂等[3]构建了衰退设备的动态预防性维修模型；时昌明等[4]提出了根据任务强度确定维修时机的装甲装备维修计划优化模型；张晓红等[5]提出了基于退化状态空间划分的多设备系统状态维修决策模型；赵英俊等[6]提出了基于状态维修的预防性维修策略；张明亮等[7]设计了一种基于多Agent的战时装备维修保障系统。以往研究中，研究领域大多聚焦于地方企业和工业部门，研究对象大多考虑单装(设)备维修计划，对多装维修计划制定的研究不够深入。然而，装备维修计划的制定和一般设备设施维修计划的制定略有区别，装备效能和军队战斗力息息相关，因此对于装备维修计划制定更多地偏向于提升效能，对维修效益重视程度不如地方企业，而且“双控”维修模式也是针对装备领域提出的；考虑到装备都是成体系运用的现实情况，在制定维修计划时，一方面要考虑效能衰减对于装备可用度的影响，另一方面要尽可能的提升装备体系效能。因此，本文基于“双控”维修模式，从多装角度出发，以装备体系效能最大化为目标，建立了多约束条件的装备维修计划优化模型，采用粒子群算法求解，通过示例验证了模型和算法的有效性。

1 问题分析

装备维修计划制定一般是多条件约束下的决策和优化问题，计划的编制者要从宏观上去整体把握，要考虑诸多影响因素，比如经费限制、时间要求、修理级别、修理能力、任务可用度等。本文对问题做出一定简化，即一个年度内，总共存在若干装备，基于“双控”维修模式，考虑装备效能随时间衰减以及维修使装备效能得以恢复，在满足若干约束条件的情况下，计划编制者来决策哪些装备需要维修、什么时候维修，以实现年度内装备体系效能的最大化。

假设1装备都还有维修的价值，不存在装备要退役不修理的情况。

假设2装备的使用频率是一致的，不考虑装备使用频率高导致效能衰减快、使用频率低导致效能衰减慢。

假设3不考虑跨年度修理的情况，所有的维修任务都是在一个年度内完成的，一件装备在一个年度内最多只考虑一次修理。

假设4在“双控”维修模式下，对于某件装备，在修理级别确定后，修理范围和修理深度也就随之确定，装备的维修工期和维修经费根据历史数据得出确定值，不考虑加大资源投入导致的工期缩短、经费增加，不考虑装备在维修时状态不同而导致维修经费不一样。

2 建模与描述

2.1 装备效能衰减模型

近些年来，关于武器装备效能评估方法的研究有许多，常用的装备效能评估方法包括层次分析法、Lanchester方程法、模糊综合评判法、ADC法、SEA法等[8]。效能评估要么从静态的角度去看待装备效能，认为装备效能评估出来就是一个固定的值，要么基于战场环境和作战任务的变化来动态评估装备效能。本文的装备效能是装备战技性能指标的一种综合体现，装备在实际使用过程中，不考虑维修的情况下，装备的各项性能指标会出现下降的趋势，即装备效能应该是随时间衰减的一个函数。这种衰减特性是固有的，不管其衰减的方式和曲线是什么样的，其衰减的趋势是造成装备需要维修甚至退役的根本原因[9]。

实践证明，装备在使用过程中，随着使用时间增加，装备的各项性能指标都会存在不同程度的下降，这就必然会导致装备效能的下降。从装备的整个使用阶段来看，在装备使用初期，装备的各个零件较新、磨损较少，各项性能指标都会维持在一个较高的水平，故障发生率低，因此效能衰减的较慢；在装备使用中期，装备的各个零件都出现了不同程度的磨损和老化，各项性能指标均会出现下降的趋势，故障发生率也会提高，因此这段时间效能衰减较快；在装备使用末期，如果不考虑修理的情况，装备效能已经在一个比较低的水平，因此效能衰减的速度又会放缓。总结起来，效能P随时间t的函数曲线如图1所示。

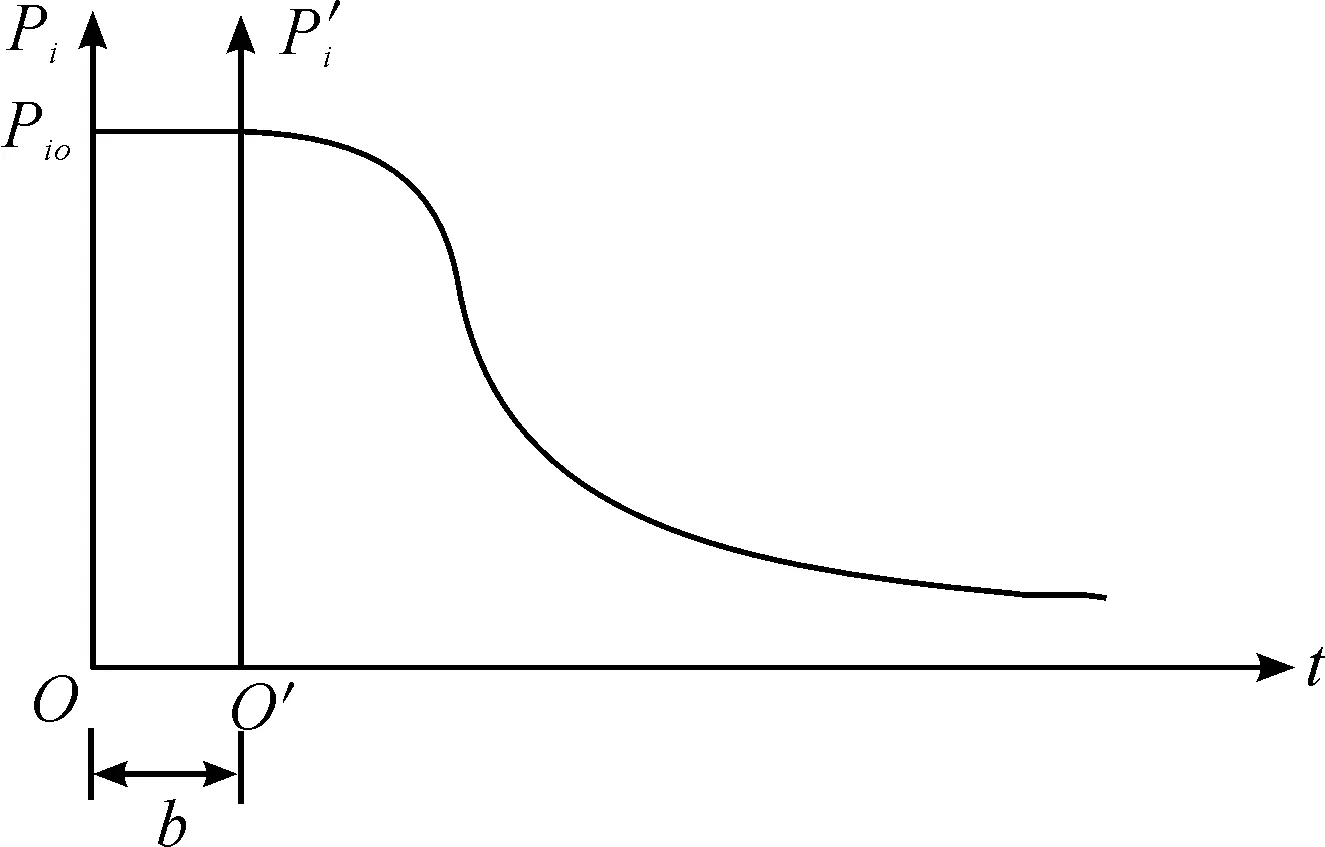
图1 装备效能衰减函数曲线

经过分析可知，在不考虑维修的情况下，装备效能随时间呈S型递减。联想到逻辑斯谛函数是描述资源有限条件下种群增长规律的S型递增函数，为了方便接下来的分析，对逻辑斯谛函数进行适当变化，假设装备效能函数为：

(1)

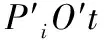
(2)

在装备的实际使用过程中，不会任由装备效能像图1中的趋势发展下去，当装备效能下降到一定程度时，就应该终止使用。因此必须要制定装备i使用效能下限Pi min，当效能衰减至下限值时，就应该终止该装备的使用。装备的终止使用，也就意味着装备能够发挥的效能为0，此时装备效能函数曲线如图2所示。

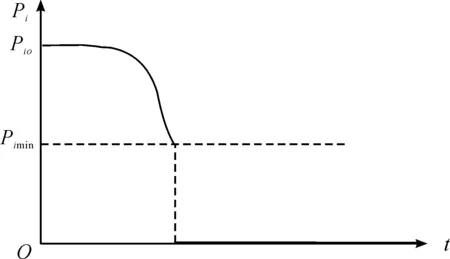
图2 考虑效能下限的装备效能衰减函数曲线

考虑使用效能下限的效能函数为：

(3)

以上都是没有考虑装备维修的情况，实际上，任何装备在使用一段时间后，都会进行维修，否则就是失修的状态。装备维修会使效能得到一定程度的恢复，效能衰减速率恢复初始状态，装备维修所能恢复的效能ΔPi应该是关于维修经费c和维修时间t的正相关的一个函数，即维修经费和维修时间越充足，装备所能恢复的效能越大，用数学模型表示就是ΔPi=f(c,t)。在“双控”维修模式下，根据假设条件4，装备的维修工期和维修经费根据历史统计数据得出确定值，可以认为该件装备维修所能恢复的效能ΔPi是一个固定值。另外，在装备维修的这段时间内，由于装备无法使用，装备的效能为0。总结起来，考虑维修情况的装备效能函数曲线如图3所示。

考虑维修的效能函数为：

(4)

2.2 装备维修计划优化模型

对于装备体系效能的评估，主要分为解析法和系统仿真法两大类，解析法包括指数法、ADC法、效能指标综合法等，系统仿真法包括EA法、ABMS法、SD法等[10]。由于本文研究重点不在体系效能，对其进行简化处理。

假设A、B、C装备是同类型装备，这些装备的能力是相似的。当它们成体系作战时，它们的装备体系效能应该在各个装备效能之和基础上再乘以一个强化系数。对于几者的不同组合形式，强化系数也是不同的，那么同类型装备体系效能为：

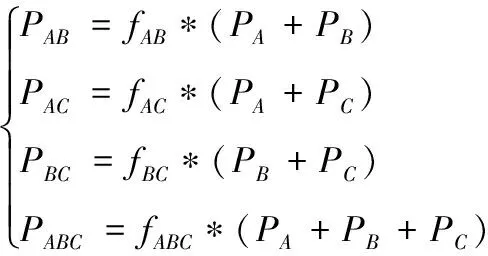
(5)

式(5)中:fAB、fAC、fBC、fABC分别是各个组合的强化系数，且都是数值大于1的数。3件装备的强化系数fABC的数值要大于两装备的强化系数fAB、fAC、fBC。

用Pi(t)表示装备i考虑使用效能下限和维修时的效能函数，目标就是使n件装备在一个年度内体系效能达到最大化，函数模型为：

(6)

式(6)中，f值根据能够使用的装备组合的不同取不同的强化系数。

经费约束表示为：

(7)

xi为0时，表示装备i不修理；xi为1时，表示装备i需要修理。ci表示装备i的维修经费，C表示总的预算经费，要修的装备的总维修经费要低于总的预算经费。

维修工期约束表示为：

(8)

维修都是在本年度完成的，不考虑跨年度修理的情况，也就是维修起始时间大于0，维修结束时间小于12。模型表现形式为：

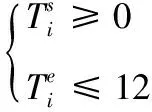
(9)

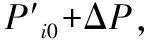
(10)

由式(10)可知，计划编制者在决策何时开始修理时，修理起始点装备i所处效能应低于Pio-ΔPi，也就是在装备效能没下降ΔPi之前，装备还处于比较良好的状态，此时不应该进行维修，否则会造成不必要的浪费。

在实际执行任务的维修保障工作中，为降低任务期间装备的故障风险、提高可靠性、减少故障风险损失，因此需要对装备在执行任务期间制定一个效能使用下限，约束模型为：

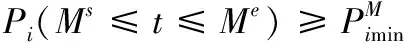
(11)

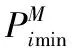
装备是军队形成战斗力的基础，要保证军队在任何时间都有一定数量的装备可用，不能在一个时间段内同时进行维修。模型表现形式为：

(12)

式(12)中：Nt表示t时刻处于修理状态的装备数量；r表示装备需要达到的完好率。

3 粒子群算法求解

本模型所要求解的结果是装备是否需要修理以及装备修理的起止时间，装备是否修理是0-1规划问题，起止时间的确定是高维连续优化问题。粒子群算法是一种并行的、高效的、全局搜索的方法，既可采用二进制编码，也可采用实数编码，因此比较适合本模型的求解。具体步骤如下。

步骤1编码方式。

采用分段编码方式，前半段是二进制编码，只取0和1，表示装备是否进行维修；后半段是实数编码，表示装备维修的开始时间，取值范围为[0,12]，对应现实中的1月到12月，比如取值在[0,1]范围内表示1月份。其染色体编码如图4所示。

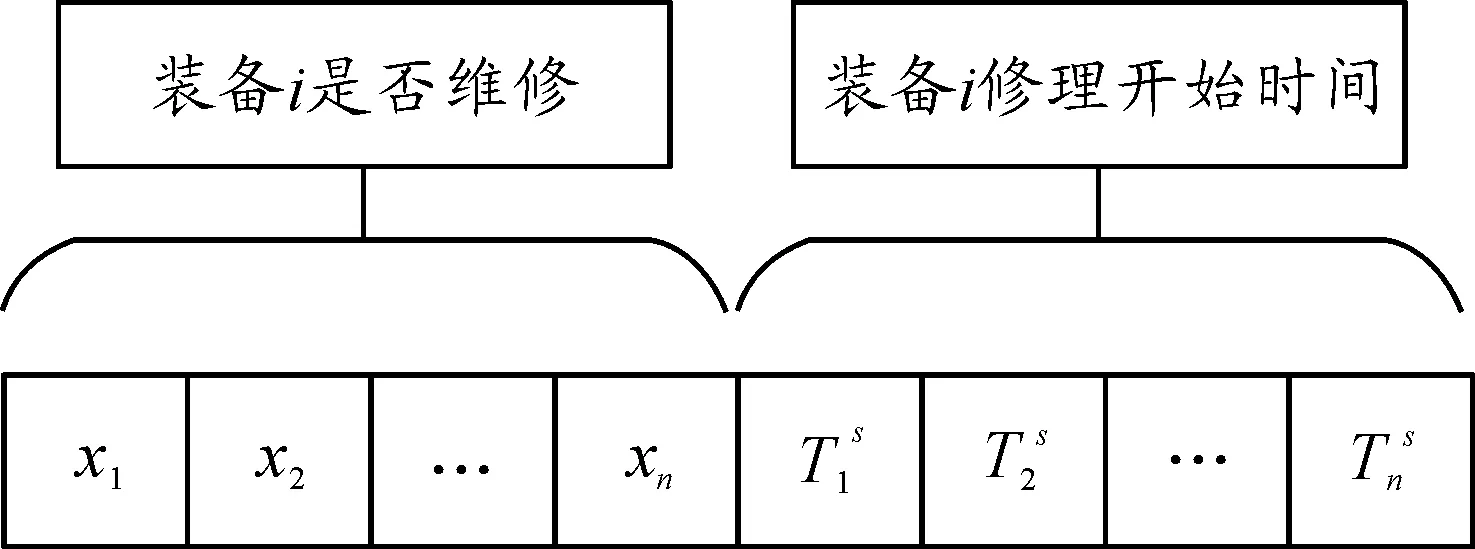
图4 粒子编码方式示意图

步骤2初始化各项参数。

初始化群体粒子个数N、迭代次数T、种群的初始位置x、种群的初始速度v、粒子个体最优位置p和最优值pbest、粒子群全局最优位置g和最优值gbest，设定了学习因子c、惯性权重w、位置最大值Xmax最小值Xmin、速度最大值Vmax最小值Vmin等参数。

步骤3适应度函数。

模型中的目标函数是使n件装备在一个年度内体系效能达到最大，因此可直接把目标函数作为粒子群算法中适应度函数。由于模型中对是否维修和维修起始时间做出了一定的限制，对于不满足模型约束的粒子，可采用罚函数的思想，使该粒子的适应度值为0而被淘汰。

步骤4速度更新公式。

速度更新公式为：

v(t+1)=w*v(t)+c1*rand*(p-x)+

c2*rand*(g-x)

(13)

式(13)中，rand为[0,1]区间上的随机数。同时为了防止粒子的速度过大而直接跳过优秀区域，对粒子在每一维的速度都限制在[Vmin，Vmax]内，对于超过速度范围的粒子，则重新对该粒子的速度进行初始化。

步骤5位置更新公式。

由于前半段采用离散编码，粒子每一维的位置取值只能是0和1，速度的每一维代表位置每一维取1的可能性。因此离散粒子群算法中的速度更新公式不变，其位置更新公式表示为：

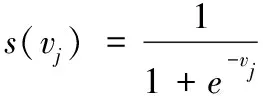
(14)

(15)

后半段采用连续编码，其位置更新公式为：

x(t+1)=x(t)+v(t+1)

(16)

对于超出了[Xmin，Xmax]位置范围的粒子，对其进行异步处理，即对超出位置范围的维度重新进行初始化，其他的维度保持不变。

步骤6迭代优化。

按照前面的步骤进行迭代优化，当达到最大迭代次数后，结束搜索过程，输出最优值。

4 示例分析

某基地今年有装备维修费1千万，有5件装备。装备完好率r要求为60%以上。装备5要在7月1日至7月30日期间执行任务，任务要求装备5的效能使用下限为100。

体系效能的强化系数f运用模糊评价法得出：

f12=1.108 2，f13=1.013 8，f14=1.197 7，f15=1.050 2

f23=1.063 1，f24=1.060 1，f25=1.008 4，f34=1.103 6

f35=1.051 2，f45=1.081 7，f123=1.389 5，f124=1.383 9

f125=1.224 2，f134=1.318 4，f135=1.271 9

f145=1.343 9，f234=1.304 7，f235=1.252 2

f245=1.298 6，f345=1.371 2，f1234=1.617 3

f1235=1.459 7，f1245=1.447 2，f1345=1.511 1

f2345=1.658 7，f12345=1.862 8

在控计划和经费的“双控”维修模式下，修理级别按照修理周期及相关维修规定进行确定，对于已经完成过修理的装备，维修经费和维修工期可按照历史维修数据确定。对于首次进行修理的新型装备可按照相近装备确定或按照订货合同价的相应比例予以测算。效能函数当中的t以各装备最近一次维修完成或者首次使用的时间为坐标原点，已使用时间是指装备首次使用或者最近一次维修之后所使用的时间。为了方便表示，表中的单位“月”都是以30天为基础。其他数据参数如表1所示。

表1 装备数据参数

装备维修计划模型优化目标为：

(17)

不考虑维修时效能函数表达式为：

(18)

考虑维修时效能函数表达式为：

(19)

约束条件为：

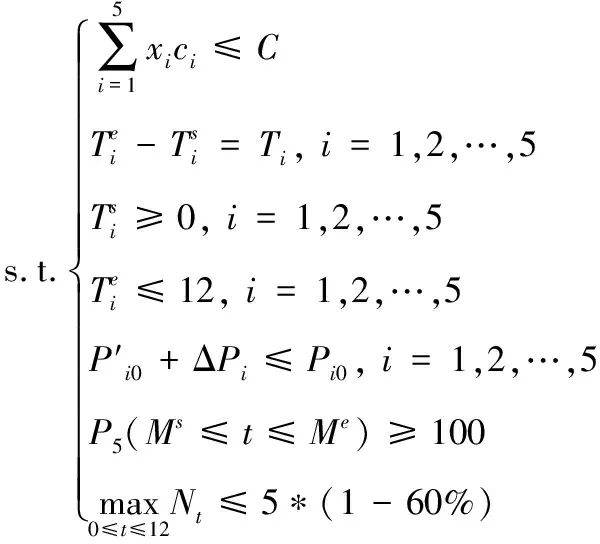
(20)

在保证装备体系效能最大化的条件下，运用粒子群算法对该模型进行计算，经过200次迭代，得到最优位置g=[1,1,1,0,1,6.20,4.34,7.04,5.92,0.77]，该位置对应的最优适应值gbest=7 440。其中适应度值变化曲线如图5所示，装备可用性曲线如图6所示，装备的维修计划如表2所示。

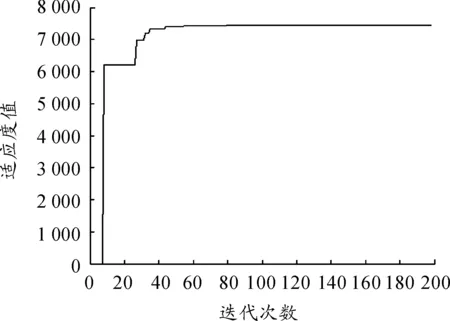
图5 算法收敛特性曲线

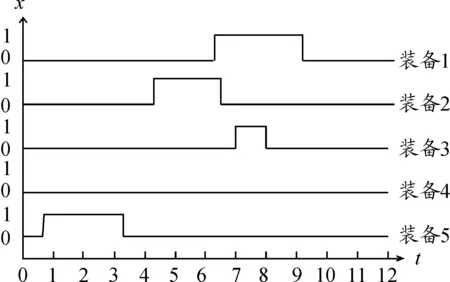
图6 装备可用性曲线

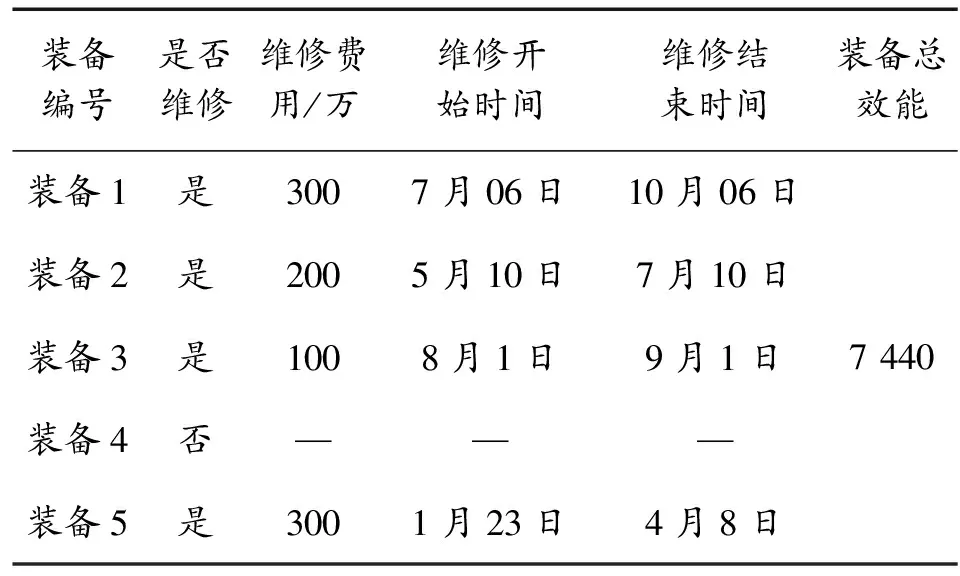
表2 装备维修计划

通过对计算结果进行分析，需要对装备1、2、3、5进行维修，装备4不维修也不会在该年度达到使用效能下限，也就是说不会出现失修的情况。可以发现，得出的结果满足了模型中的各项约束条件，并得到了相对较优的装备体系效能，有效解决了装备维修中的多约束目标优化问题，为装备维修计划的制定者提供了一定的参考依据和借鉴意义。

5 结论

提出了装备效能衰减模型，对体系效能模型进行了简化处理。结合装备维修计划模型，以一个年度内装备体系效能最大化为目标，满足经费约束、维修时机约束、装备完好率约束、任务条件约束，制定出了装备维修计划。

考虑一个年度内的维修计划制定，最多考虑一次维修，可在本模型的基础上，延长年限，在更长的时间跨度内制定装备维修规划。另外，还可进一步研究其他维修模式对于装备效能的影响，并对比不同维修模式对装备维修计划制定的影响。