复合调制雷达波形低截获性能分析

王亚涛，王昊飞

(中国电子科技集团公司航空电子信息系统技术重点实验室, 成都 610036)

电子侦察、干扰和反辐射导弹等技术的应用与发展使得雷达的生存能力受到越来越严重的考验，因此对低截获(Low probability of intercept，LPI)雷达技术的研究势在必行[1]。当然，低截获雷达是一个相对的概念，它是针对某一类侦察接收机表现出一定的低截获性能，没有绝对不能被截获的雷达系统。低截获雷达的设计是要尽可能地降低被截获的可能，与此同时，低截获雷达所采用的信号形式应尽量复杂，并增大信号的不确定性，使其即使被截获后也不易被侦察接收机提取出雷达信号特征，因此，雷达波形设计是实现雷达低截获技术的重要手段之一[2-3]。当前，雷达低截获波形主要通过采用具有大时宽带宽积的信号并利用脉冲压缩技术来取得信号处理增益，典型的信号有线性调频信号、相位编码信号以及频率编码信号等[4-6]，但是此类单一调制的信号的调制样式很容易被识别。当前典型的调制类型识别方法主要有时域分析法、频域分析法以及时频域分析法等[7-16]。相位差分法是一种常用的时域分析法，可以通过分析信号的瞬时频率来对单载频信号、线性调频信号、频率编码信号等常用的雷达信号进行调制类型识别。在频域分析法中，基于循环自相关函数与循环谱的方法可以对信号的循环平稳特性进行分析，能够得到信号的调制参数信息。时频分析法是对传统频域分析法的一种推广，通过分析信号的时域和频域二维分布特征来获得信号的脉内调制信息。为了提高雷达波形的抗调制识别性能，运用两种或两种以上的单一调制方式对发射波形同时调制而获得的复合调制波形已经成为LPI雷达波形设计的研究热点[17-20]。本文给出一种脉冲内部采用频率相位复合调制而脉冲之间调制样式都不同的复合调制信号，这种信号的特点是波形设计灵活、随机性强，使雷达能够实现距离高分辨的同时具备优良的低截获和抗识别性能。

1 频率相位复合调制信号模型

频率相位复合调制雷达信号波形如图1所示，一个脉冲内包含N个子脉冲，子脉冲间进行频率编码，fn=f0+iΔf，其中fn为第n个子脉冲的载频，n=0,1,…,N-1，i=0,1,…,N-1，且n不一定等于i，f0为子脉冲起始频率，Δf为子脉冲间频率步进阶梯，N个子脉冲的合成带宽为NΔf；各子脉冲内进行相位编码，采用P位伪随机相位编码序列，且各子脉冲内相位编码可以不同，第n个子脉冲内相位编码为cn0,cn1,…,cn(P-1)。令每个码片宽度为τc，各子脉冲宽度为τs，脉冲宽度为τp，则频率相位复合调制信号的数学表达式为：

(1)

图1 频率相位复合调制单脉冲信号波形示意图

为了实现更高的雷达距离分辨率，还可以在脉冲之间采用频率步进的方式合成更大带宽的信号，如图2所示，各个脉冲内部所采用的频率编码和相位编码样式也不相同。

图2 频率相位复合调制多脉冲合成宽带信号示意图

对于图2所示的频率相位复合调制合成宽带信号，其信号模型可以表示为：

exp[j2π(fcl+fbn)(t-lTr)]

(2)

式(2)中，clnp为第l个脉冲的第n个子脉冲内的相位编码；fcl为第l个脉冲的脉冲载频；l为脉冲串序号，l=0,1,…,L-1，L为合成大带宽信号的脉冲个数；fcl=fc0+lΔF，ΔF为脉冲间频率步进阶梯，L个脉冲的合成带宽为LΔF；fbn为各脉冲内的子脉冲基带频率；Tr为脉冲重复周期；Tf为一帧信号持续时间，即L个脉冲持续时间，Tf=LTr。

由图1和图2可以看出，频率相位复合调制信号通过进行脉内和脉间调制可以获得大时宽带宽积，即在脉冲内采用多子脉冲调制方式，子脉冲间采用频率编码，子脉冲内采用相位编码，且各子脉冲可以采用不同的相位编码类型；在脉冲间采用频率步进可以合成更大带宽信号。频率相位复合调制信号的特点是波形设计灵活、随机性强，即可以采用频率编码、频率捷变、相位编码和码型捷变的方式，使雷达具备优良的低截获和抗干扰性能。

下面从模糊函数的角度，对采用频率相位复合调制信号的雷达探测性能进行分析。由于其信号复杂度比较高，相应模糊函数解析解的推导比较困难，因此本文采用数值计算的方法进行模糊函数的分析，该方法通过FFT和IFFT快速算法来实现模糊函数的卷积运算。

在频域计算信号s(t)的模糊函数表达式为：

FFT[S(f-ξ)S*(f)]

(3)

进行数值计算时，先计算信号s(t)的频谱，然后分别将其延迟不同的ξ值，两者相乘再做傅里叶变换。

下面利用式(3)对频率相位复合调制信号的模糊函数进行分析，仿真参数如表1所示。

表1 频率相位复合调制信号仿真参数

根据表1参数，可以得到频率相位复合调制信号的模糊函数图如图3所示。

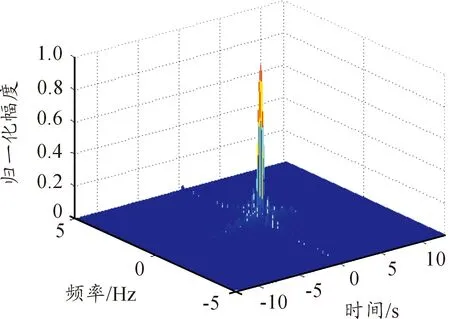
图3 频率相位复合调制信号模糊函数图

由图3可以看出，频率相位复合调制信号的模糊图呈近似的“图钉型”，具有较高的距离和速度分辨率。

2 基于STFT的脉内调制识别特征提取

本文利用文献[11]中介绍的方法，基于STFT处理对雷达信号的脉内调制类型进行分析。该方法选取的识别特征参数包括：STFT分析时间窗的频率个数、STFT瞬时频率序列均方差、STFT瞬时频率序列自相关峰值个数和STFT瞬时频率序列直方图连续性。

1) STFT分析时间窗的频率个数。只有频率分集信号的该特征大于1，可以较好地区分频率分集信号和其他信号；

2) STFT瞬时频率序列均方差。只有单载频信号的该特征接近0，可以较好地区单载频信号和其他信号；

3) STFT瞬时频率序列自相关峰值个数，只有相位编码信号的该特征值大于3，可以区分相位编码信号和其他信号；

4) STFT瞬时频率序列直方图间断次数，频率编码信号的该特征值大于1，可以用于区分线性调频和频率编码信号。

以上4个特征的仿真结果如图4所示。

图4 基于STFT的特征提取结果

3 修正的基于STFT的脉内调制识别流程

为了能够识别频率相位复合调制信号的脉内调制类型，本文对以上算法进行修正。对于频率相位复合调制信号，其瞬时频率序列自相关的结果与单一相位编码信号的结果相近，因此在将相位编码信号与其他信号区分开后，可以采用瞬时频率序列均方差作为特征参量，重新选定门限来对单一相位编码信号和复合调制信号进行区分。修正后的脉内调制识别方法流程如图5所示。

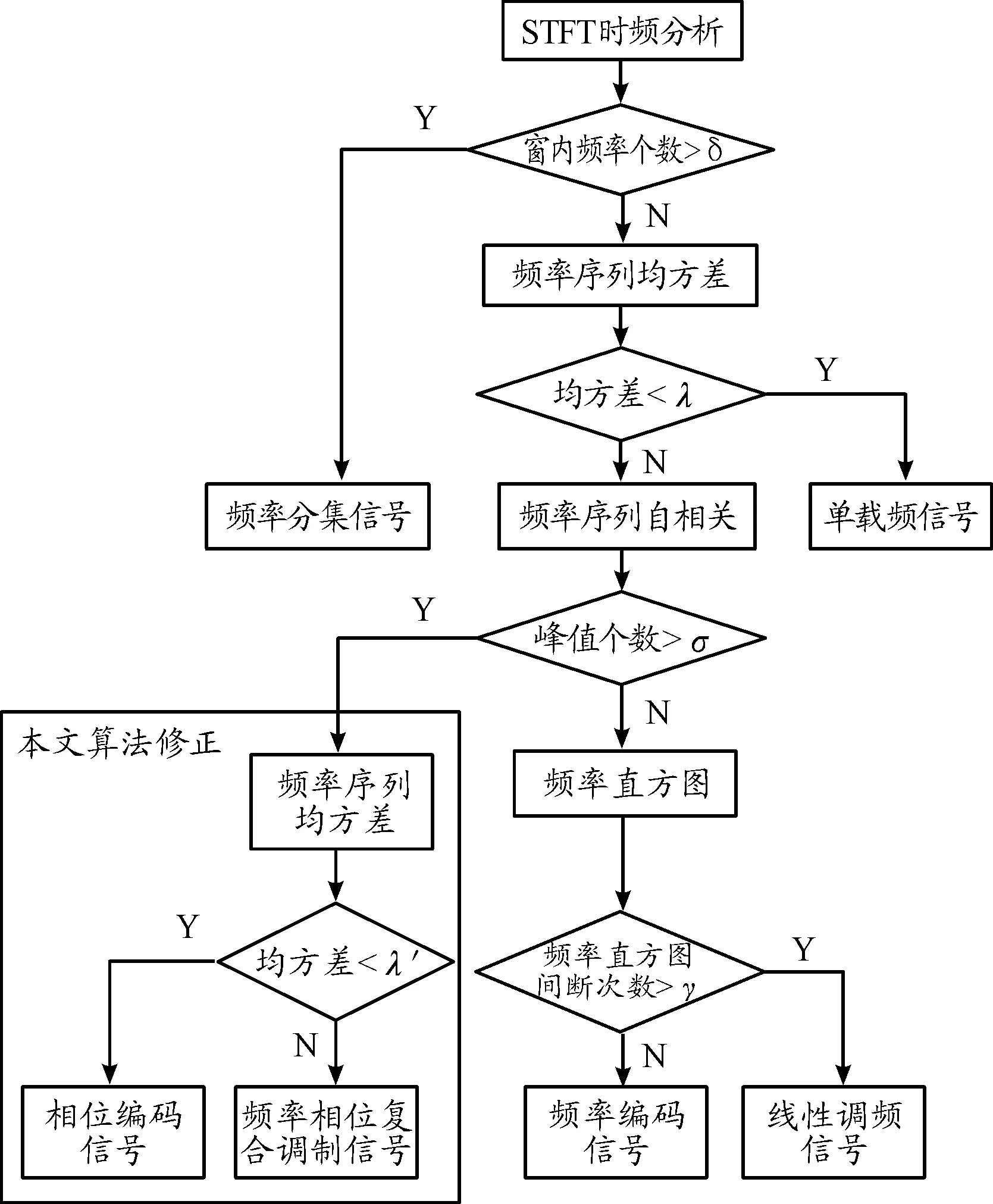
图5 基于STFT的脉内调制类型识别流程框图

4 仿真分析

本节对以上介绍的雷达信号脉内调制类型识别方法进行仿真，分析利用该算法对几种典型雷达信号特别是复合调制信号的脉内调制识别性能。仿真时首先对每种脉内调制信号独立产生1 000个脉冲，然后在不同信噪比的情况下，进行类型识别仿真计算。图6所示为不同信噪比下对各种波形的脉内调制识别概率的统计结果。

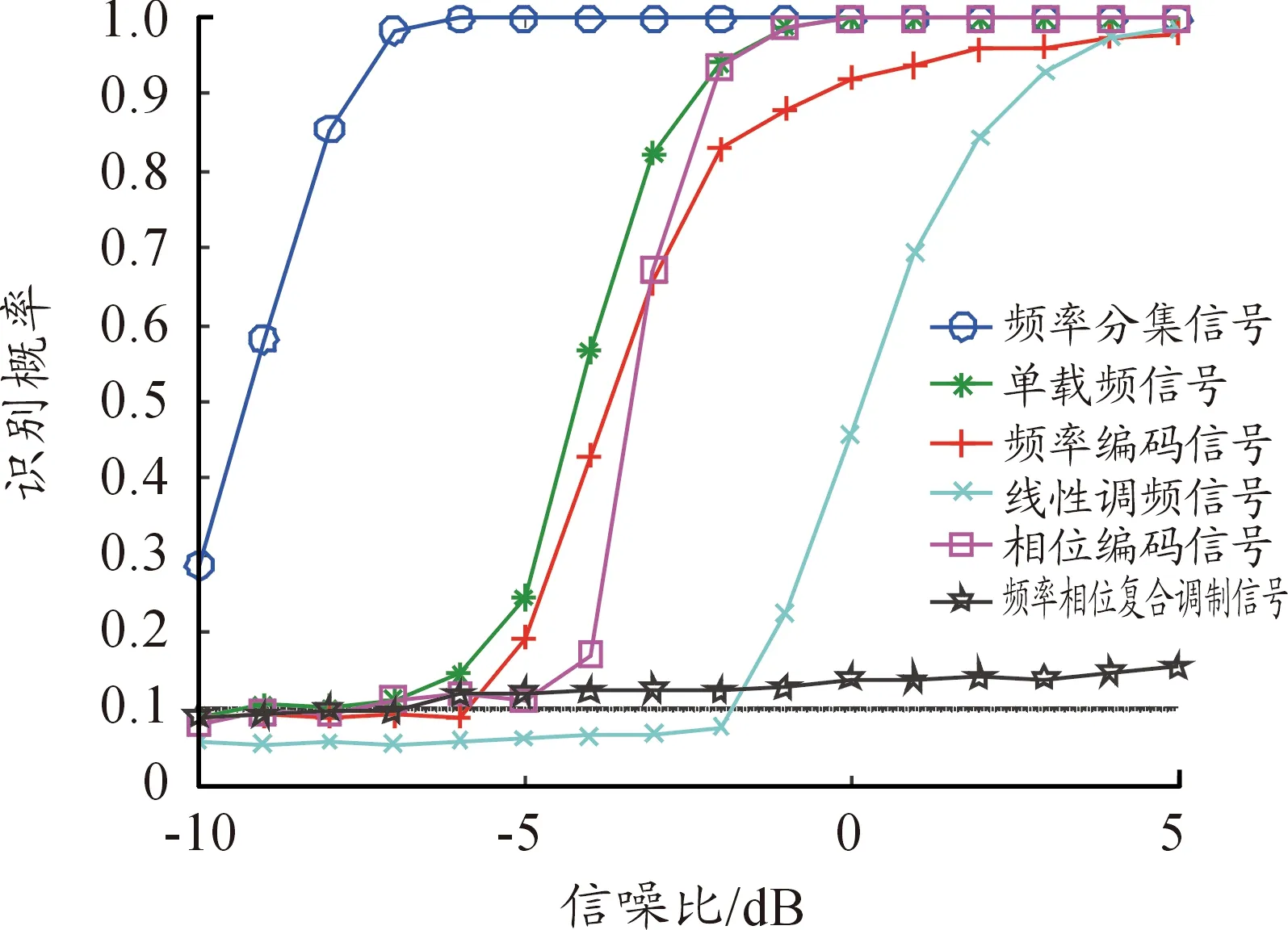
图6 不同信噪比下各雷达波形脉内调制类型识别正确率

由图6可以看出，基于STFT的雷达信号脉内调制类型识别算法可以有效地识别出单载频、线性调频、频率分集、频率编码以及相位编码信号，在信噪比高于3 dB时调制类型识别正确率基本都可以达到90%以上，这与文献[12]中的分析基本一致。而对于频率相位复合调制信号，由于单个脉冲内部既有频率编码，又包含了相位编码，并且各个脉冲的调制样式可以进行随机化的设计，因此其识别正确率较低，在较高信噪比情况下识别正确率依然低于15%。

需要指出的是，虽然采用基于STFT的雷达信号脉内调制类型识别算法对于频率相位复合调制信号的识别概率比较低，但是也有文献专门针对复杂调制波形的识别进行研究，如文献[13]结合AR模型功率谱估计方法和小波变换方法给出了一种可以对脉内混合调制雷达波形进行识别的方法，并且可以达到比较高的识别概率。本文所介绍的频率相位复合调制信号的特点在于:各个脉冲之间的频率编码以及相位编码都可以是随机改变的，即相邻脉冲之间的相关性很低。因此即使侦察接收机能够分析出当前截获到的脉冲的脉内调制参数，但是利用该信息对后续截获脉冲的分选、识别以及干扰所能达到的效果仍然是有限的。

5 结论

本文给出一种频率相位复合调制雷达信号，这种信号通过脉内调制可以降低单位频带内的信号能量，同时可以通过采用频率编码、频率捷变、相位编码和码型捷变技术来增加雷达侦测信号的难度，从而进一步改善雷达的低截获性能。本文利用模糊函数理论对频率相位复合调制信号的测距测速性能进行了分析，并基于短时傅里叶变换方法对多种雷达波形脉内调制类型进行识别，仿真结果表明，由于频率相位复合调制信号随机性强，编码方式灵活多变，相比传统的雷达波形以及单一调制波形具有更好的抗识别性。后续还需要对频率相位复合调制信号的编码优化方法进一步研究，使其具备更好的雷达探测性能。