基于GA-BP算法的外弹道落点误差预测

吴朝峰，杨 臻，曹文辉，郭东海

(1.中北大学 机电工程学院， 太原 030051； 2.庆安集团有限公司， 西安 710077；3.重庆建设工业(集团)有限责任公司， 重庆 400054)

弹丸的落点误差的准确预测，对弹丸实现精确命中目标至关重要。然而在实际过程中，火控计算机处理能力有限，解算过程允许耗时较短，且传感器输出数据较真实值有一定偏差，弹道解算误差不可避免[1]。

针对上述问题，司翠平等[2]对基于毫米波探测的弹道落点估计进行了研究；赵捍东等[3]提出使用RBF神经网络逼近外弹道方程用以预报弹丸落点；冯松等[4]提出了用声学测量设备求解连发弹丸落点;马清华等[5]将弹丸落点偏差视成是当前速度、位置和待增速度的函数，并采用经网络对落点偏差进行拟合；杨小会等[6]采用攻角修正系数解算四自由度弹道模型来预测弹丸落点。柏杰锋等[7]提出了CCD与MEMS组合测量弹丸落点偏差的方法。文献[2,4,6-7]通过测量手段的不同来对弹道落点误差进行预测,而文献[3]通过逼近外弹道方程方式，相当于拟合外弹道曲线的方式，文献[5]通过拟合落点的状态进行预测，不具有时效性。本文中在考虑恒定风速外弹道基础上，建立输入层为射角、x方向风速、z方向风速，输出层为x方向落点误差、z方向落点误差的GA-BP落点误差预测模型，直接对落点误差进行预测。

1 数据处理

1.1 外弹道模型

考虑恒定风速变化的质点外弹道方程组如下：

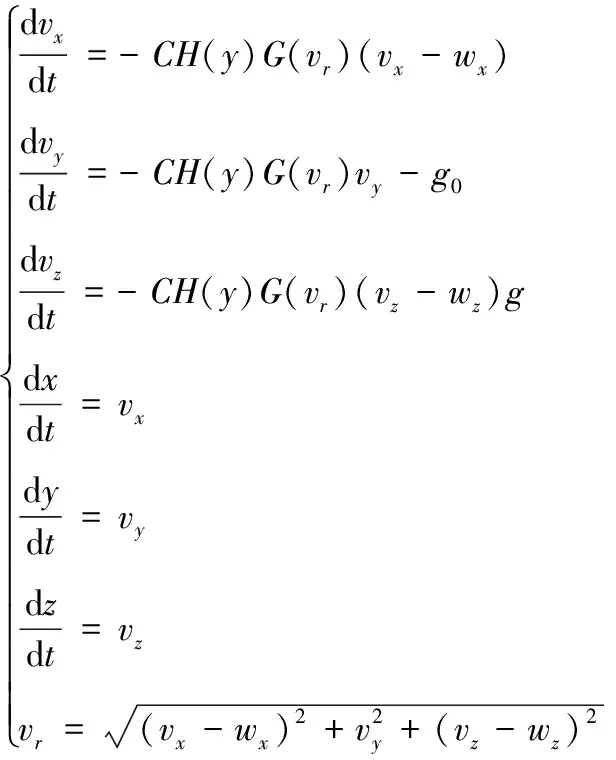
(1)

式(1)中，变量定义可参考文献[8],在此不作赘述。

1.2 数据

外弹道计算所用初始数据来自文献[8]，M46式130 mm加农炮,其弹丸初速为930 m/s,弹道系数为0.56。GA-BP神经网络预测数据来源为根据1.1所述的外弹道公式，通过Matlab编程计算得外弹道落点坐标，与不考虑风速的外弹道落点坐标做差得到。本文仅考虑外弹道射角、x方向风速、z方向风速对外弹道落点误差的影响。外弹道射角从5°取到45°每隔5°取一次，横向风速从1 m/s取到10 m/s每隔1 m/s取一次值，纵向风速从1 m/s取到10 m/s每隔1 m/s取一次值，共计900组数据。从其中随机取20组数据作为测试数据样本，其余880组数据作为训练数据样本。表1为基于遗传算法的BP神经网络仿真的测试数据样本，训练数据样本由于其数量过多在此不一一列举。

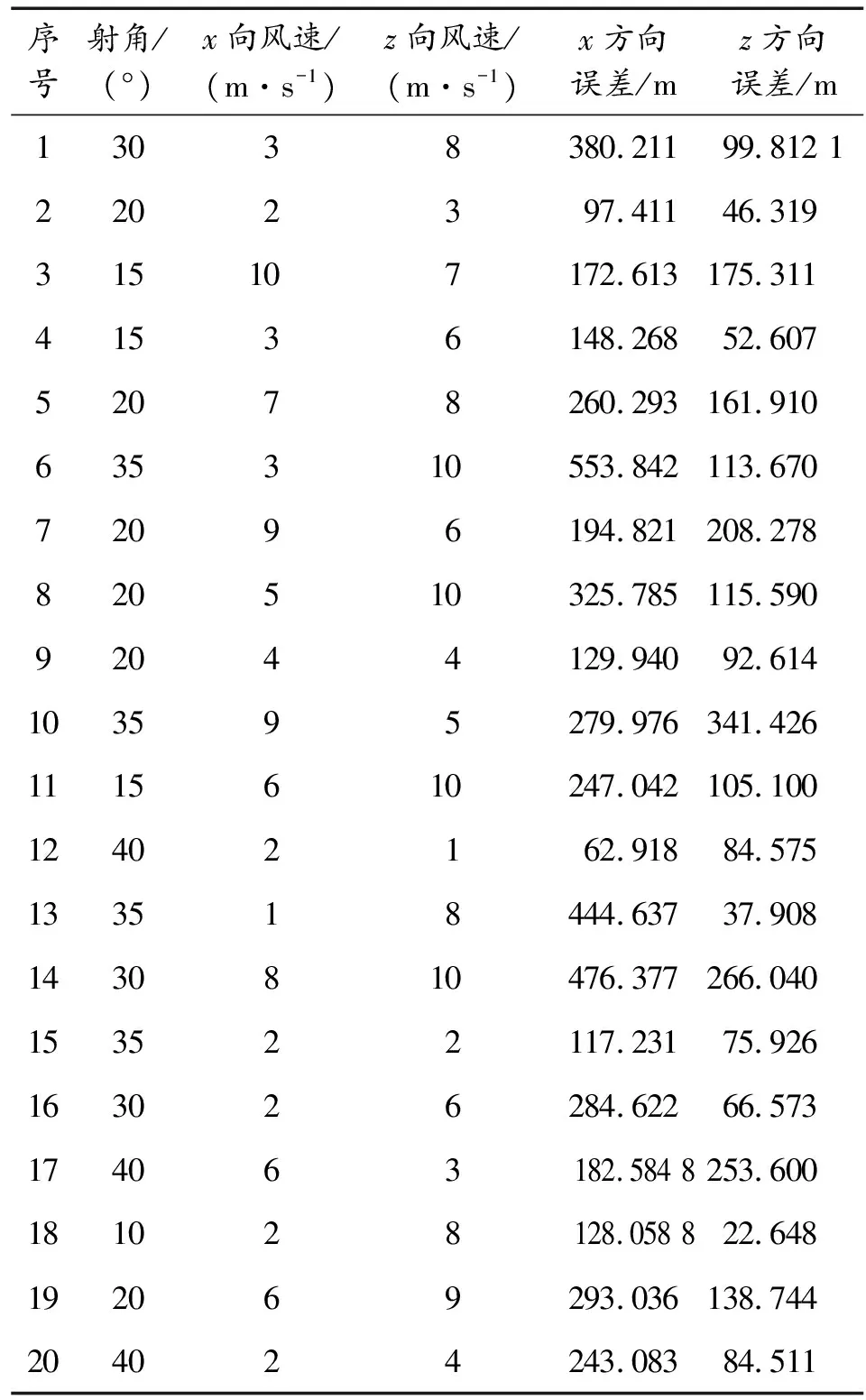
表1 测试数据样本

1.3 数据归一化处理

BP神经网络进行数据训练前训练数据样本需要进行归一化处理，其目的取消各维数据间数量级差别，避免因为输入输出数据数量级差别过大而造成网络预测误差较大。BP神经网络常用归一化数据处理方法，有最大最小法与平均数方差法，采用Matlab中的mapminmax函数对数据进行归一化处理，公式如下：

(2)

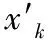
2 GA-BP神经网络

2.1 BP神经网络

BP神经网络采用基于梯度下降和误差反向传播的学习方法[9]，从图1可以看出其流程。BP神经网络训练目标是使训练样本的范数最小，BP神经网络具有非线性拟合、自学习的能力。

BP神经网络虽然是人工神经网络中用最广泛的算法，但其也存在着一些缺陷：

1) 学习收敛速度过慢;

2) 不能保证收敛到全局最优点，易陷入局部最优点；

3) 网格结构不易确定，网格的初始连接权值和阈值的选择对神经网络影响很大，但又无法准确获得。

2.2 GA算法

GA算法(遗传)是一种高效、并行、全局搜索的算法。基于GA算法的BP神经网络用遗传来确定BP神经网络的初始连接权值和阈值，提高了BP神经的学习收敛速度，避免了BP神经网络陷入局部极小的情况。 基于GA算法的BP神经网络算法流程如图2所示，把BP神经网络的权值和阈值编码作为遗传算法的种群，把BP神经网络的测试误差作为遗传算法的适应度；通过遗传算法的选择、交叉、变异等方式得出适应度最小的种群；通过解码得出测试误差最小的BP神经网络初始连接权值和阈值。

3 落点误差GA-BP预测模型

落点误差GA-BP模型选择射角、横向风速、纵向风速为网络输入层，落点的横向误差与纵向误差作为输出层，采用基于遗传算法优化的BP神经网络来实现输入层与输出层之间的映射，建立考虑恒定风速的外弹道落点误差GA-BP预测模型，如图2所示。

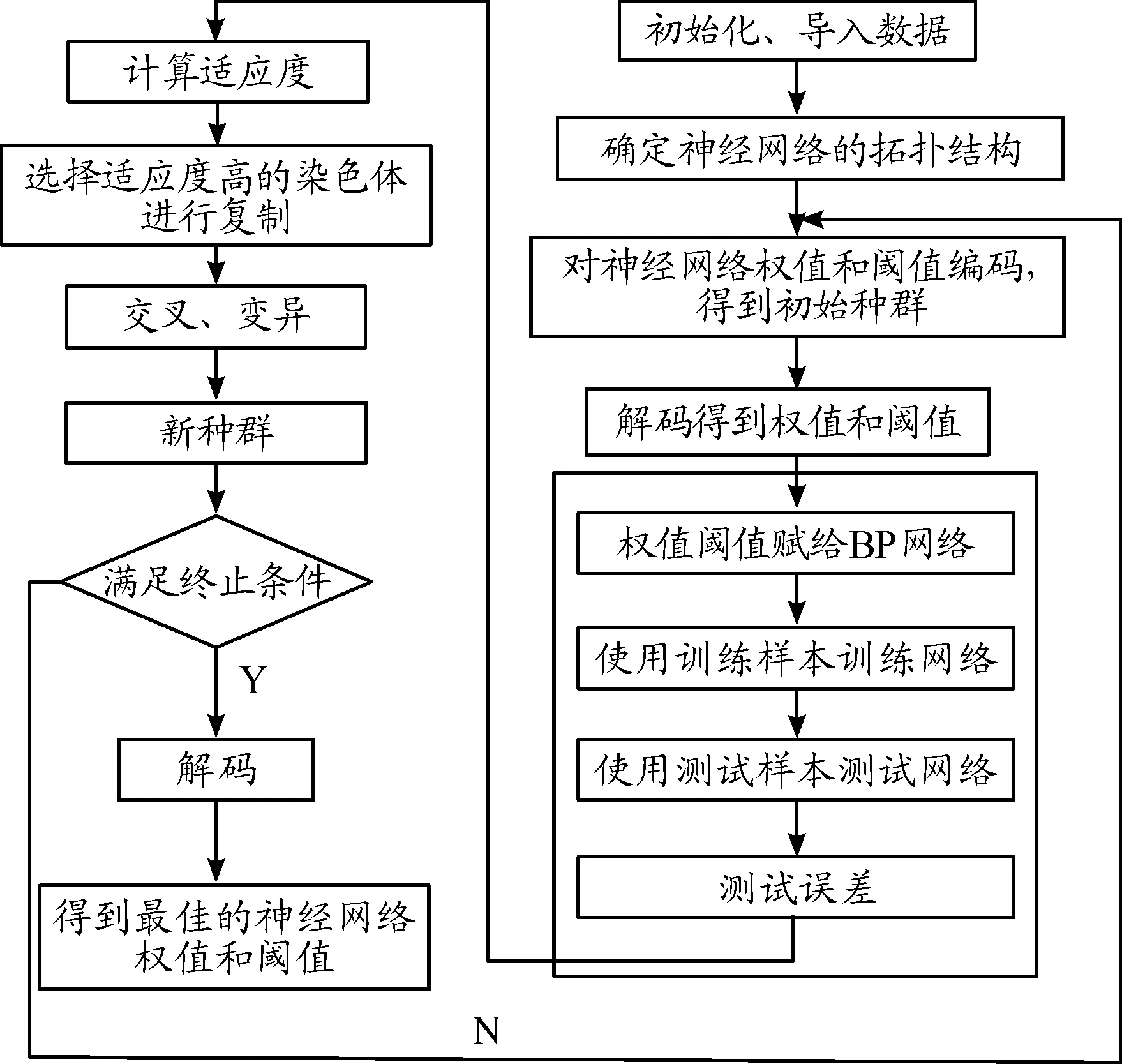
图2 GA-BP流程框图

3.1 BP网络结构的确定

理论表明，一个S型隐含层加上一个线性输出层的3层BP网络，能够逼近任何函数。因此采用一个3层BP神经网络来构建考虑风速的外弹道落点误差GA-BP预测模型。输入层为射角、横向风速、纵向风速3个参量，输出层为落点的横向误差与纵向误差2个参量。隐含层节点个数由于缺少准确的理论计算方法，一般采用公式(3)计算出大致的值，并在此基础上进行BP神经网络试算，得到一个预测误差较小的隐含层节点数。

(3)

式(3)中:k为隐含层节点数;n为输入参量个数;m输出参量个数;α为1到10的数。

通过试算最终选择隐含层节点数为7个，同时输入层到隐含层传递函数采用logsig函数，隐含层到输出层传递函数采用purlin函数。

3.2 训练参数的设定

训练参数的设定对神经网络至关重要， 其直接影响网络的性能。经过对BP神经网络的反复试算，设定训练次数为2 000，学习速率为0.000 1，训练期望误差为0.001。

3.3 GA算法参数设定

采用英国谢菲尔德大学开发的遗传算法工具箱对BP神经网络的初始权值与阈值进行优化。对权值和阈值进行二进制编码，得到遗传算法种群，然后对种群进行适应度计算、选择、变异、交叉得到适应度最小的最优个体；最优个体解码得到BP神经网络的初始连接权值和阈值。设置遗传算法的种群个体为40，交叉概率为0.7，变异概率为0.01，最大遗传代数为100，代沟为0.95。

3.4 仿真结果分析

按以上参数设定后进行遗传优化计算，得到每代最优解(即适应度函数最小解)，适应度函数与进化代数关系曲线如图3。

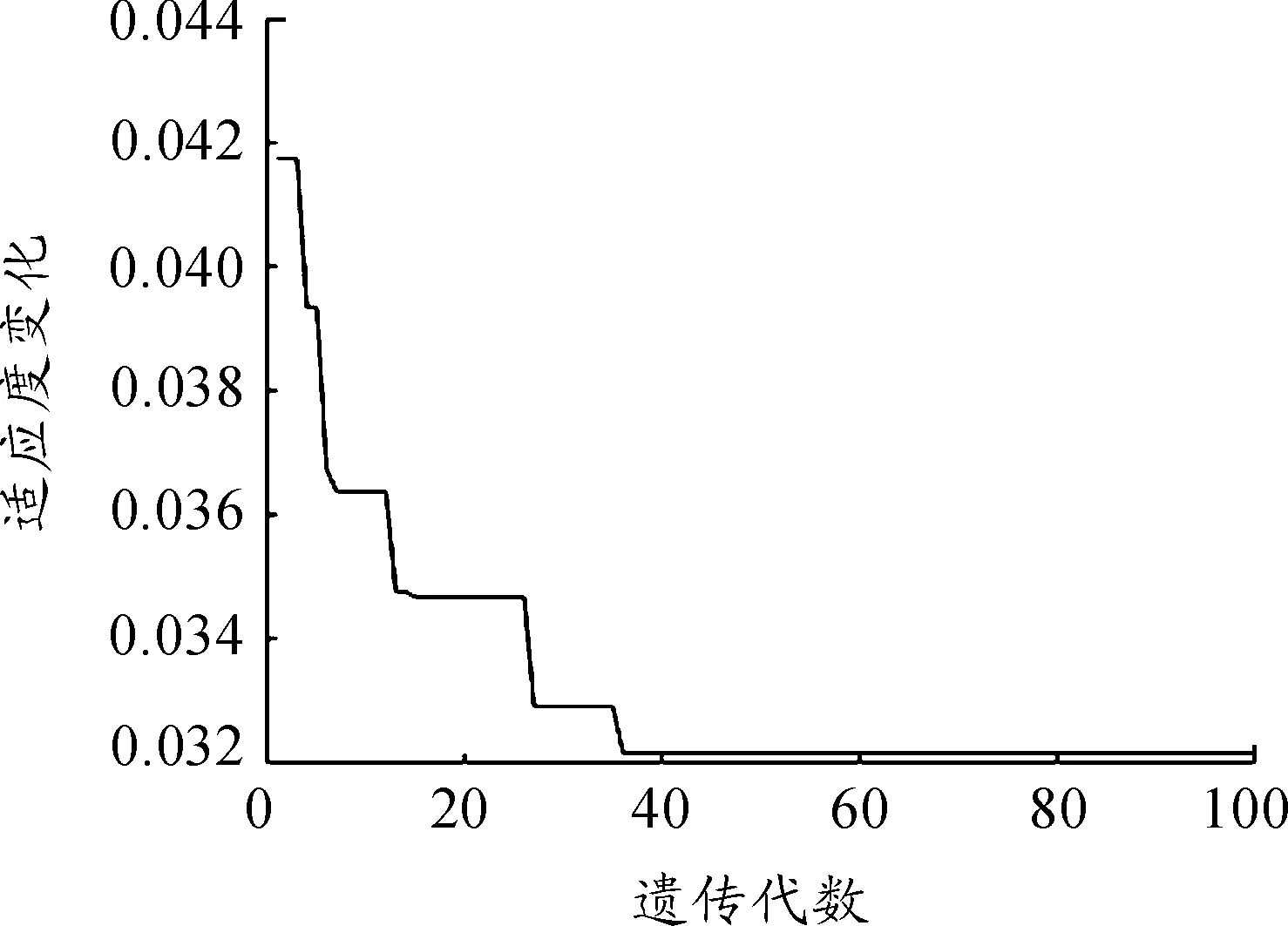
图3 适应度曲线

由图3中可以看出，前13代适应度函数变化较为明显，13～44代适应度函数变化较小，44代以后可以认为函数已经收敛到最小值。优化后的BP神经网络初始连接权值和阈值矩阵如表2所示，表2中，w1为输入层到隐含层的连接权值，w2隐含层到输出层的连接权值，θ1为隐含层阈值，θ2为输出层阈值。

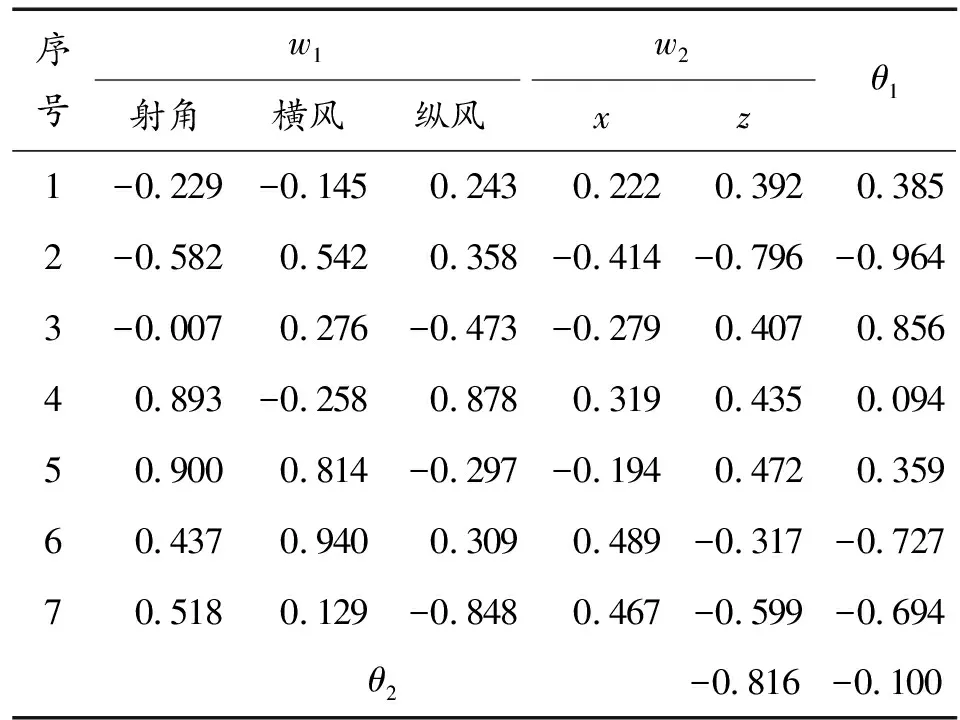
表2 优化后权值与阈值矩阵

按照3.2节中的参数设置，对比采用随机网络连接权值和阈值的BP神经网络与采用遗传算法优化后的网络连接权值与阈值的BP神经网络对测试数据样本进行预测，归一化处理后的样本误差如表3所示，预测误差如表4所示。

从表3得出训练样本与测试样本误差，GA-BP模型较BP模型均有很大程度减小。

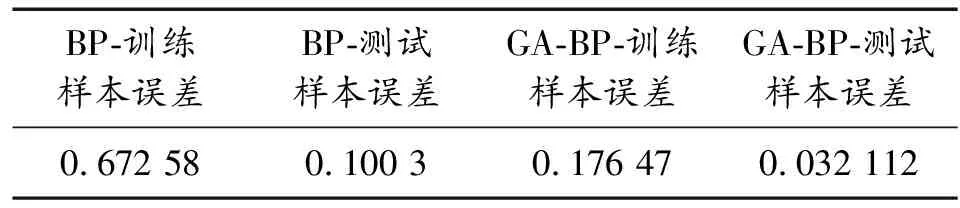
表3 归一化处理后的样本误差

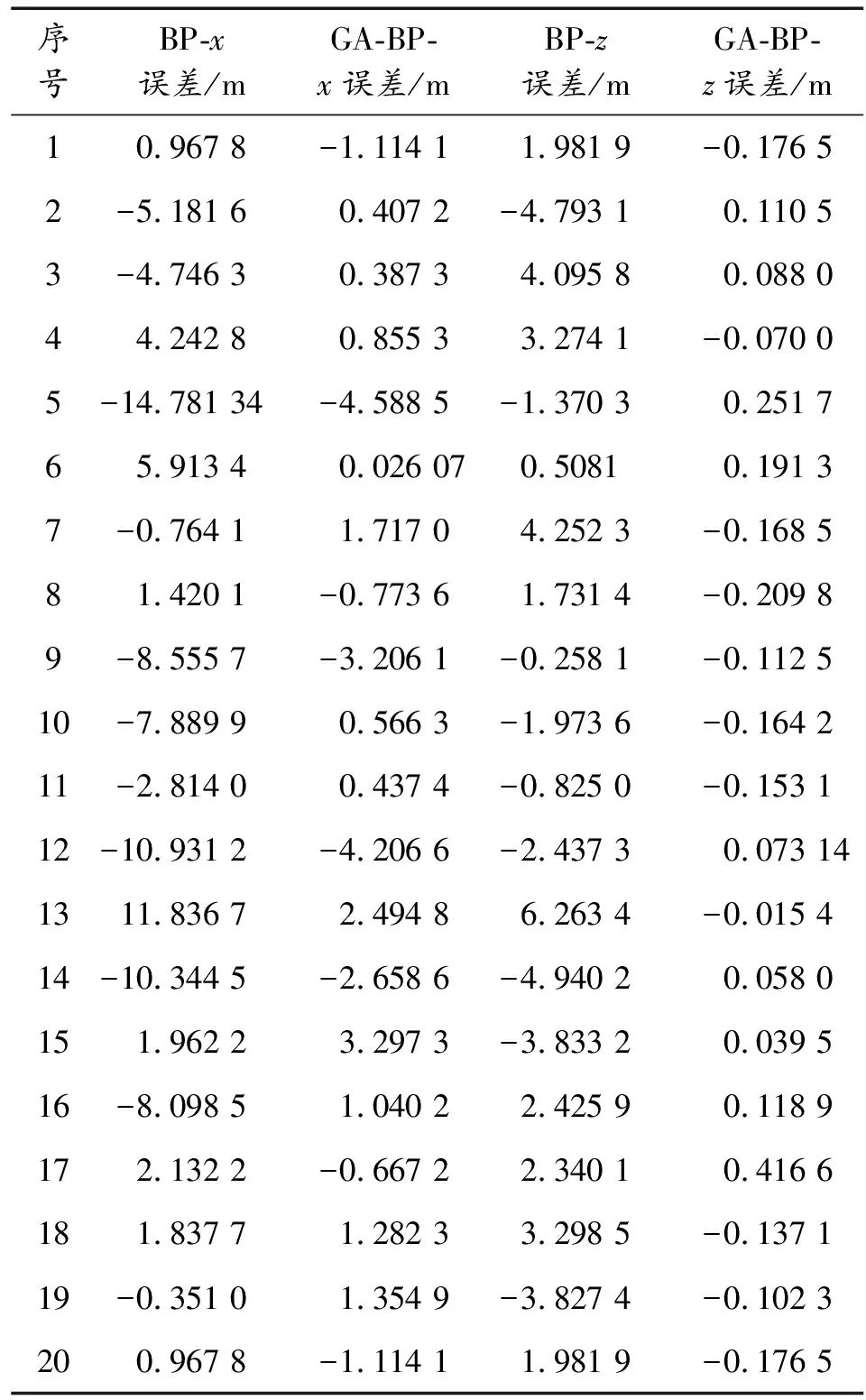
表4 预测误差

从表4可以得出，GA-BP预测模型较BP神经网络预测总体误差更小，大部分样本的误差降低，个别样本误差有一定程度的增加，这是由于遗传算法优化时取整体误差作为适应度函数的结果。对比样本预测的x方向相对误差如图4，z方向相对误差如图5。

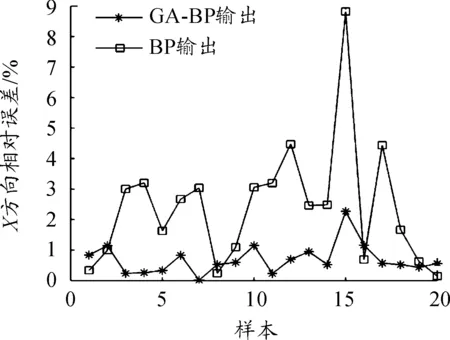
图4 x方向相对误差

从图4可以得出，x方向BP神经网络的预测相对误差平均值为4.51%，样本的最大相对误差为4.51%，优化后的BP神经网络预测误差平均值为0.79%，样本的最大相对误差为2.08%；从图5可以得出，z方向BP神经网络的预测相对误差平均值为5.32%，样本的最大相对误差为10.93%，优化后的BP神经网络预测误差平均值为0.24%，样本的最大相对误差为1.94%。

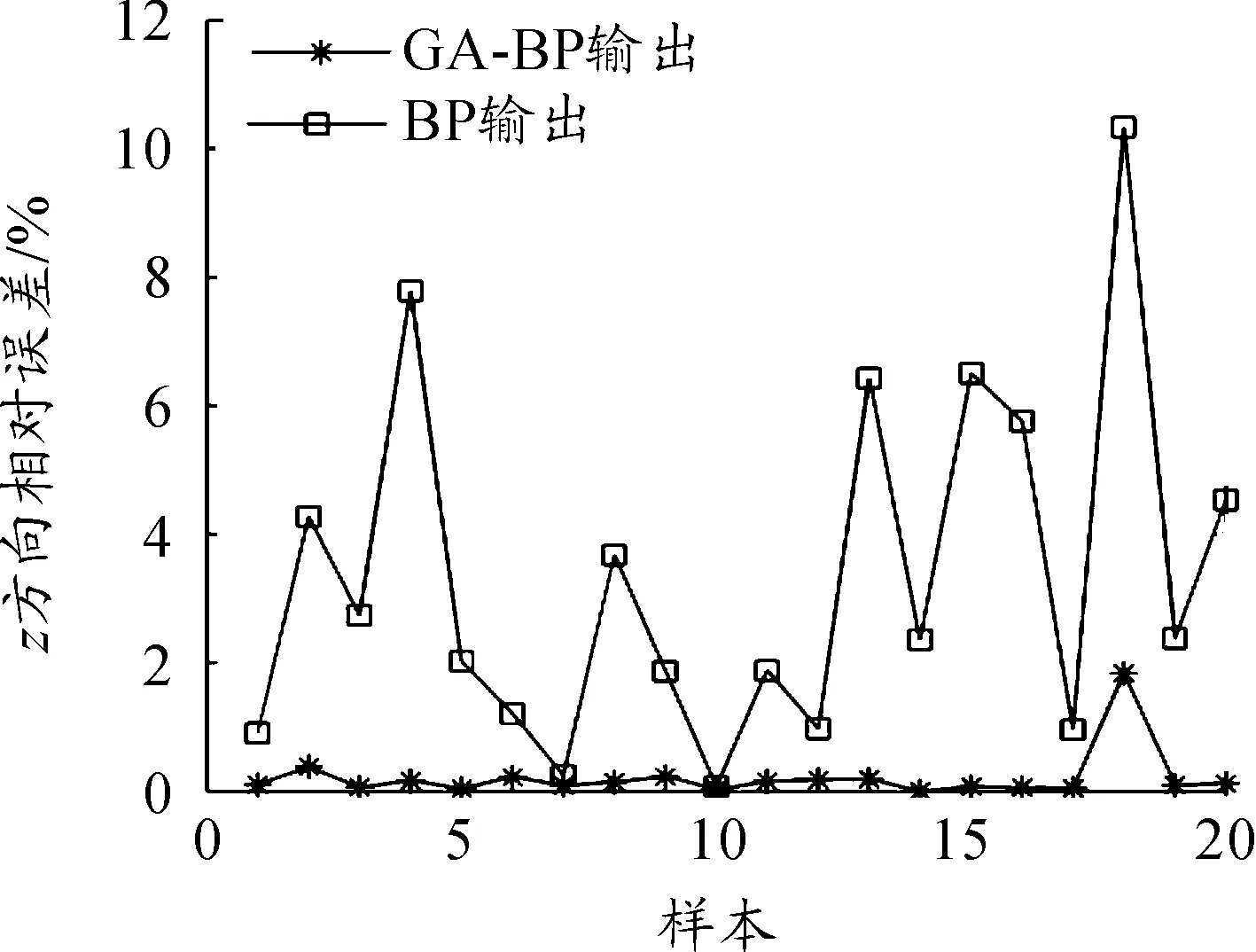
图5 z方向相对误差

4 结论

1) 针对恒定风速下外弹道落点误差预测手段较少的情况，提出了基于GA-BP神经网络风速外弹道落点误差预测模型。

2) 将GA-BP外弹道预测模型与仅用BP神经网络的预测模型作比较，GA-BP落点误差预测模型较BP神经网络预测模型，x方向的预测相对误差平均值减小了3.72%，相对误差的最大值从8.84%降至2.08%；z方向的预测相对误差平均值减小了5.08%，相对误差的最大值从10.93%降至1.94%。这表明GA-BP神经网络能较为准确的预测考虑风速的外弹道落点误差，为外弹道落点误差的研究提供较为可靠方法。