寻的制导旋转导弹比例导引

李克勇,王波兰

(上海机电工程研究所,上海 201109)

采用雷达/红外导引头的寻的制导方法被广泛应用于先进的战术导弹上[1-2]。同时,为对抗高机动目标,具有更高俯仰控制效率的鸭式布局也通常被选用,而鸭舵的下洗作用导致导弹滚转通道的控制能力低下,难以有效实现滚转方向的控制,使弹体绕其纵轴连续周期滚转不仅能够避免该问题,而且更重要的是可以简化控制系统,减少传感器数量,降低生产成本。例如RIM-116导弹,由于采用了旋转体制,只需一对鸭舵即可进行全方位控制,而且减少了制导雷达天线个数。因此,对寻的制导的旋转导弹进行研究具有重要的意义。

不同于其他常规弹体,采用旋转体制的导弹在制导控制方面存在一定的特殊性。弹体旋转引起俯仰和偏航通道的运动耦合,导致弹体可能出现不收敛的圆锥运动问题,锥形运动稳定性是旋转弹研究的主要方面,已取得了大量有重要意义的研究成果[3-7]。由于通道间存在严重的耦合作用,传统上采用的分通道独立设计的驾驶仪设计方法在旋转弹上不再适用,研究表明,旋转使得驾驶仪参数的设计稳定区域大大减小,为确保弹体的动态稳定性,提高控制系统性能,指令补偿、动态逆方法等解耦控制措施被采用[5-7]。具有低成本和精确打击能力的制导旋转射弹主要采用特征弹道跟踪和落点误差反馈修正2种制导控制策略,其导引方法和飞行动态稳定性被广泛研究[8-10]。尽管如此,对采用寻的制导的旋转导弹的相关研究还较少。

1 数学模型

采用比例导引的寻的制导旋转导弹系统框图如图1所示。导引头跟踪目标运动,使目标始终位于视场中心,输出比例导引所需的目标视线角速度和弹目距离及其导数;制导计算机结合导弹本身的运动信息,计算得到需用过载指令;控制系统将过载指令转化为相应的舵偏指令,通过驱动一对或两对鸭式舵片的偏转,使得弹体产生攻角,进而改变速度矢量的方向,使得导弹按照给定的制导规律攻击目标。

导弹的测量(主要指导引头)和执行(电动鸭式舵)装置随弹体一起旋转,因此目标视线角速度以及舵机指令均为正弦周期信号。但由于制导和控制系统响应不可避免地存在滞后和延时,在转速作用下,正弦周期信号输入的响应输出存在相位滞后;同时,弹体绕纵轴连续周期滚转将诱导产生面外力矩作用,进而引起俯仰和偏航方向动力学耦合。这些响应滞后和交叉耦合作用一方面导致导弹在执行制导指令时出现锥形运动,如果系统参数设计不合理,甚至会引起不收敛锥形运动形式的动不稳定;另一方面导致弹体输出过载不能严格跟踪理想的过载指令,进而引起较大的脱靶量。下面首先分别建立比例导引、控制系统以及弹体运动的数学描述。

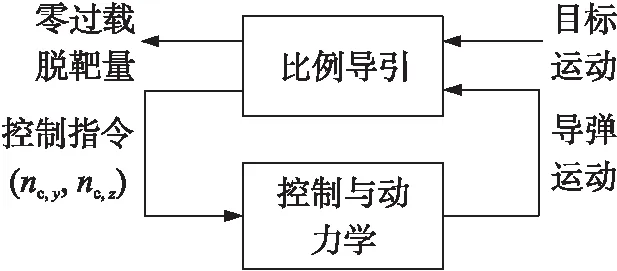
图1 采用比例导引的旋转导弹运动框图

1.1 制导方程

通常情况下,导引关系在惯性空间中被描述。但对于旋转导弹,由于导引头的测量信息与控制指令的执行都在旋转坐标系下完成,在旋转系下建立导引关系将减少信号与指令转换过程带来的误差,也更便于系统分析,因此,得到寻的制导旋转导弹比例导引示意图如图2所示。其中,下标b表示弹体坐标系,下标s表示弹体固连视线坐标系。

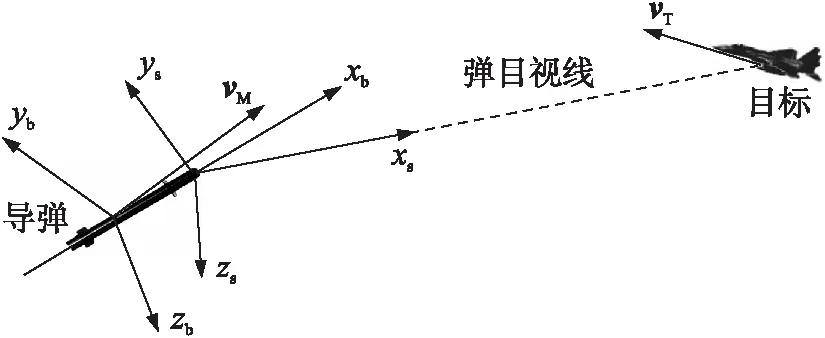
图2 寻的制导导引关系示意图

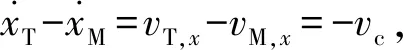
(1)

(2)

(3)

1.2 控制方程

由于省略弹体的稳定控制回路(自动驾驶仪回路),制导指令经过指令转换环节直接生成舵偏角指令,传递给舵机伺服系统,驱动执行机构作动。采用一对舵片作为执行机构的舵偏指令,即:

式中:φ0=atan2(nc,y,nc,z)为指令相位角。

假设舵机的动力学过程可等效为二阶振荡环节,其时间常数和阻尼比分别为τa和ζa,可得舵机系统的响应延迟角为

则舵机响应方程为

1.3 动力学方程

根据文献[7],弹体动力学方程可表示为

过载输出方程为

式中:α为攻角,β为侧滑角,ϑ为俯仰角,ψ为偏航角。

2 比例导引分析

为了便于分析,暂不考虑弹体控制响应过程,即令:

(4)

则式(1)～式(4)构成了寻的制导比例导引闭环系统。

2.1 视线角速度收敛

(5)

(6)

将式(6)代入(5)整理可得:

(7)

由于tgo-t>0,可求得:

从上面的过程可以看出,旋转引起弹体y轴和z轴方向上视线角速度的运动耦合,这种耦合将引起导引头测量的目标视线角呈现锥形运动形式,但并未对视线角速度的收敛情况产生实质的影响(导引关系方程中虚部系数未出现在收敛条件中);导引头跟踪目标的动力学延迟在转速作用下将产生测量滞后,滞后角度引起的动力学耦合对导引关系产生影响,使得比例导引系数的设计下限增大。在不考虑目标机动的情况下,非旋转导弹比例导引使得目标视线角速度收敛的导引系数N>2,而对于旋转导弹,则为

N>2/cosφdh

(8)

2.2 最优导引系数

在理想状态下,忽略各种误差、干扰和不确定性因素,并假设导弹过载不受任何限制,比例导引的脱靶量为0,即RTM(tgo)=0,甚至在视线角发散的情况下依然成立。尽管如此,求解最优的比例导引系数,使得在整个攻击过程中导弹的过载支出最小,具有重要意义,通常也是比例导引必须解决的问题。

将式(6)代入并整理,可得:

(9)

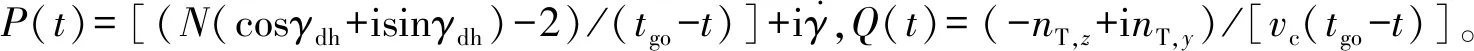
在不考虑目标机动影响时,可令Q(t)=0,对应的齐次方程的通解为

(10)

即在不考虑目标机动时,目标视线角速度的变化规律如上式所示。

将式(10)代入式(9),可得:

目标函数取极小值,则∂J/∂N=0,可得最优比例导引系数N=3/cosγdh。可以看出,由于旋转引起导引头跟踪目标时存在动态延迟角,最优比例导引系数比在非旋转情况下的3要大。

2.3 仿真验证

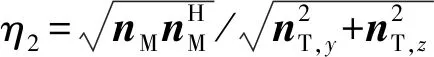
图3 初始误差条件下无量纲加速度与导引系数的关系

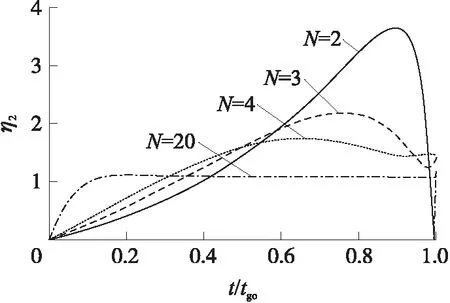
图4 目标机动时无量纲加速度与比例系数关系

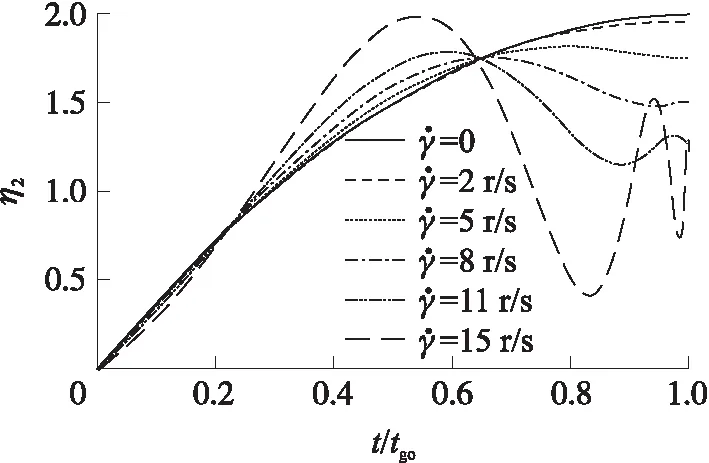
图5 不同转速无量纲加速度变化情况

3 锥摆运动分析

导弹的制导、控制与动力学方程构成了一个闭合的回路,系统方程各部分都存在俯仰和偏航方向的交叉耦合,其动态响应必然呈现锥形运动的形式。比例导引部分存在显著的非线性和参数时变性,不失一般性,在弹道特征点上对时变系数作固化处理,即各部分系数与系统变量无关,且在系统响应过程不随时间变化;同时忽略目标运动的影响,将目标机动作为系统输入,在考虑稳定性问题时,不失一般性,可令输入为0。

通过案例数值仿真,可得弹体旋转对比例导引系数设计稳定域的影响如图6所示。从图6中可以看出,在整个导引过程中,弹体的转速越高,比例导引系数N的设计稳定域越小。在本算例中,当转速大于8 r/s,N取任何值都几乎不能使得导弹在导引过程中锥形运动稳定。

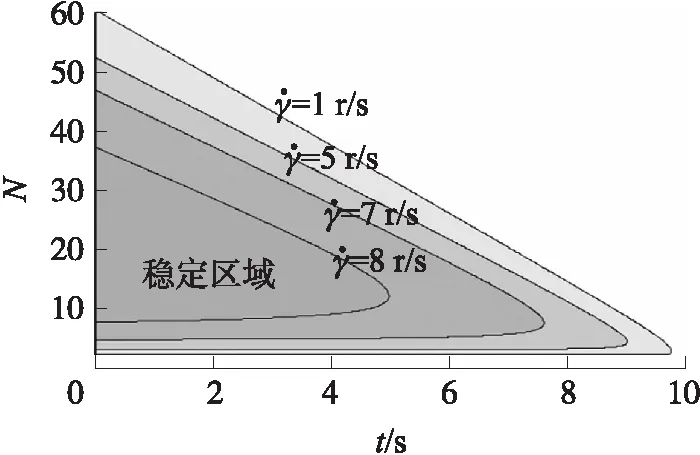
图6 比例导引锥形运动响应

在锥形运动不收敛或是收敛很慢的情况下,弹体在惯性空间呈锥摆状态飞行。此时,弹体的控制负载增加,更容易引起饱和非线性;锥摆运动导致飞行速度快速衰减,影响导引段制导律的执行效果;锥摆运动将引起更多的扰动问题,直接影响末制导精度。

锥摆运动对寻的比例导引制导精度的影响如图7所示。图中,ΔX为脱靶量。随着弹体转速的升高,导弹的脱靶量呈指数形式增加。转速升高,弹体的耦合作用增强,弹体的锥形运动稳定域减小,导致在整个导引过程中不稳定飞行时间大大增加,进而使得制导精度严重下降。

图7 比例导引脱靶量与弹体转速的关系

4 结束语

本文研究了一种寻的制导的单通道控制旋转导弹的比例导引问题,与非旋转导弹相比,由于存在俯仰和偏航通道的交叉耦合作用,视线角速度收敛对应的导引系数和最优导引系数均变大,同时在整个导引过程中使得视线角速度收敛的稳定域变小。转速越高,导引系数的设计稳定域越小,导致视线角速度提前发散,弹体呈现锥摆飞行状态,进而导致脱靶量大大增加。数值仿真表明,在给定比例导引系数条件下,脱靶量随转速呈指数形式增加。