基于时间重定标的人类行为时间特性成因研究

卞正宇，杨 丹，朱世玲

(南京邮电大学 计算机学院，江苏 南京 210003)

0 引 言

对于人类行为模式的研究一直是复杂性科学研究的热点。在处于大数据时代的当今社会，海量的数据由人类活动产生，也势必要将其应用于对人类行为的研究[1]，由此产生了人类动力学，而人类活动时间分布特性的研究是其中一个重要的组成部分。在研究的初期，学者们认为人类活动的时间特性应当表现为泊松过程，即两个相继行为间隔的时间大体相近，很长的时间间隔应当指数级般的少见。但在2005年，Barabsi A发表在《自然》杂志的研究显示[2]，人类行为时间间隔分布对于经典泊松过程偏离，反而可以用幂函数进行很好的拟合，进一步研究发现，绝大部分的人类行为都具有幂律的特性[3-5]。在此基础上提出的基于任务系统，基于人类兴趣、记忆，基于人类社交属性等的模型都是对幂律分布成因的探索[6-12]。有研究发现，幂指数随个体活跃性度的提升单调变化，这表明个体之间活跃度的异质性对于人类行为时间间隔分布具有一定的影响。为了研究这种普遍性质的形成因素，结合过往的时间重定标算法，文中提出了一种改进算法，以消除个体活跃度的差异对于时间间隔分布的影响。实验结果表明，虽然活跃度的异质性可以影响幂指数的大小，但幂律性质的发生是人类内禀属性决定的。

1 幂律特征

过去人们认为人类行为发生的时间间隔分布服从泊松分布，最初是泊松在审判案件时为了引入概率的概念提出的。但是近年来随着大数据技术的发展，大量人类活动产生的数据沉积下来，这些宝贵的财富为学者们的研究提供了坚实的基础，摆脱了过去缺乏数据的窘境。通过这些数据，对人类行为时间间隔的研究发现绝大部分的行为的时间间隔分布和等待时间分布都符合幂律特性，而不是想象中的泊松过程[13-14]。幂律特性是指时间间隔t的概率分布为幂函数，即：

p(t)∝t-α

(1)

例如，电子邮件的时间间隔分布为p(t)∝t-α，α∈(1.2,1.7)任务执行的分布为p(t)～t-α，α∈(1.47,1.74)，网页访问行为服从p(t)∝t-α，α∈(2.1,3)，twitter数据服从p(t)∝t-α，α≅1.35，等等。

这说明人类活动的时间间隔可以有一些很大的数值，即存在长时间的等待，而不是如泊松过程所想的，时间间隔分布均匀，且不允许长时间的空白。这在数学上表现为在泊松过程中，间隔时间的分布曲线的尾部按照指数下降，而幂律分布具有胖尾的特征，即在尾部下降的远不如指数快。经过大量的实证研究显示，幂律分布的时间间隔分布可能是人类行为的普遍性质，且其形成原因可能是由于人类的自主性与内禀特性。幂律分布还有另外一个广为人知的名字叫28法则，即人类活动许多系统中都可以分为20%和80%两个群体，例如20%的人掌握了80%的财富，股市中只有20%的人可以保持盈利，80%的人会亏损。由此可见幂律分布不仅仅存在于人类行为的时间间隔中，它在人类为主导的系统中也普遍存在，甚至在自然界中也大量存在。例如地震的间隔时间、小行星带中陨石的分布也符合幂律分布。让人不禁感到世间万物好像都冥冥中服从同一个规律，到底是什么导致了这种普遍特征的产生也是目前研究的热点。

2 活跃度

人类活动个体活跃度H被定义为单位时间内活动发生的频率[15]，即:

(2)

其中，N为该个体总的行为次数；T为第一次与最后一次行为之间的时间间隔。

在日常生活中，活跃度表现出明显的周期性与波动。一个繁忙的上班族在工作时间中接到电话的频率可能为1个小时一通，拨出电话的频率可能是一个小时8通，但是在午夜2点他通话行为的频率将会大幅度降低，这就造成了活跃度的波动。日复一日的工作大同小异，这时活跃度会表现出以天为周期的周期性。如图1所示，赵志丹等研究了AOL数据集[16]，选取10天的数据，其中横轴为行为发生的时间，纵轴就是在该时刻发生行为的个体的数目。通过图1可以发现，用户的活跃度呈现出明显的周期性与较大的波动，同时对于不同活跃度的用户进行的分布研究表明，用户行为时间间隔的幂指数随活跃度的上升而增大。

图1 AOL用户活跃度的周期与波动

在日常生活中这种活跃性的周期性大量存在，例如用户访问互联网网页、用户编辑维基百科、玩家登陆在线游戏、研究人员向Linux服务器提交计算任务、用户通过手机进行搜索等等。同时还有研究显示行为时间间隔也存在着周期性，比如家庭出游通常以一周为周期，直观的解释就是一家人通常在周末外出娱乐。同时最近的一项研究表明，用户在线观看视频的时间间隔也存在周期性现象。

3 时间重定标方法

3.1 典型的时间重定标方法

为了研究用户活跃度对于幂律分布形成的影响，Radicchi等[17]提出用间隔时间的平均值〈t〉来将横轴间隔时间t改为t/〈t〉，纵轴概率密度函数p(t)改为p(t)〈t〉，从而研究不同活跃性用户的行为机制。这就是一种常见的时间重定标方法，所谓时间重定标即是对时间尺度重新定义。

最近的一项研究[6]根据Netflix数据集，选取三组不同活跃度的用户，使用上文的时间重定标方法，分别对这三组数据做了处理，结果如图2所示。

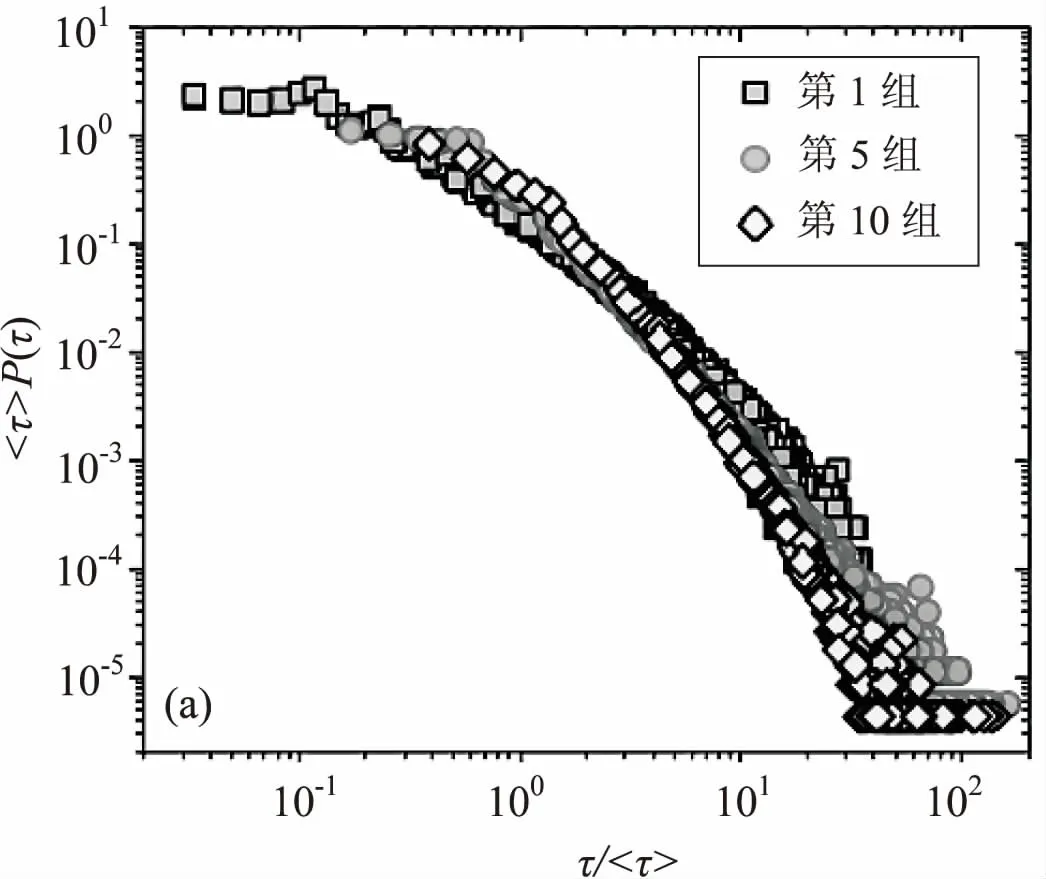
图2 不同活跃度用户时间重定标处理结果

从图2可以看到，三组数据经过时间重定标处理后几乎坍塌重叠，这说明不同活跃性的个体可能拥有相同的内在行为特性。

3.2 改进的时间重定标方法

由于用户活跃度的影响，在某一小段时间内，行为发生的次数非常多，而在另一段时内，行为发生的次数却非常少。为了消除这种影响，需要寻找一种方法可以使得时间在事件发生快的时候流逝的更快，在事件发生慢的时候流逝的慢一点，自然转向重新定义一种时间尺度标准。因此有研究者提出了一种新的方法“相对时钟法”[18]，用个体相继两个行为之间，同一时区其他个体发出的行为总数来度量时间间隔长度，从而消除活跃度周期性带来的影响，取得了很好的效果。

但是相对时钟法只侧重于消除活跃度周期性的影响，没有考虑到个体总体活跃性对幂律指数的作用。文中结合相对时钟法与3.1中的算法，提出一种新的算法，选取用户两个相继事件间隔的时间中其他用户发生事件的总数与用户自身平均时间间隔倒数的乘积作为新的时间尺度，即该用户两个事件的时间间隔。具体的算法步骤如下：

Step1：计算个体行为的平均时间间隔〈t〉;

Step2：计算各个相继事件发生的时间内其他用户发生的事件数N;

Step3：选取N/〈t〉作为该用户各相继事件的时间间隔t。

平均时间间隔〈t〉是个体自身活跃性的体现，而事件数N是活跃度周期性与波动的一个表现，选择N/〈t〉作为时间间隔，既消除了活跃度周期与波动的影响，又体现了个人内在的活跃性特性，从而研究个体行为时间间隔幂率分布的成因。

4 实 验

4.1 数据集

4.1.1 AOL

AOL(American Online)数据集是由美国在线提供，它是一家提供互联网服务和媒体服务的公司，该数据集包含从2006年3月10日至2006年3月20日的互联网用户搜索行为记录，时间精度为秒。

4.1.2 Delicious

Delicious是一个帮助用户管理和分享他们喜欢网站链接的网站，提供了一种简单共享网页的方法，它为互联网用户提供管理和分享他们喜欢的网页书签功能。该数据包含了 123 449名用户，6 279 896条书签记录，以及1千万条标签信息，该数据时间精度为天。

4.2 实验结果与分析

实验采用AOL和Delicious数据集，在MATLAB上对数据进行了分析。首先在两个数据集中分别选取10个不同活跃度的用户，分析他们的行为时间间隔分布，采用最大似然估计法分别得到这十个用户的真实时间间隔分布的幂率指数。表1给出了在两个数据集上不同活跃度的用户基于真实时间的时间间隔分布，其中用户的活跃度随组号而增加。通过表1可以观察到AOL、Delicious两个数据集上用户的真实时间间隔分布都可以由幂律分布很好地拟合，并且时间间隔分布的幂指数随个体的活跃度单调增加。

接着采用文中提出的改进算法对刚刚选出的用户数据进行操作，得到的结果如表2所示。表2是经过时间重定标算法处理的结果，其中用户的活跃度随组号而增大。通过表2可以看到经过处理后实验结果仍然服从幂律分布，并且幂指数依然随个体的活跃度单调增加。

表1 不同活跃性用户真实时间间隔的幂指数

对比表1与表2可以发现，在消除了活跃度周期与波动的影响后，结果却仍然表现为幂律分布。这些结果非常明显地表明用户间隔时间分布的幂律现象并不能由用户活跃性的异质性和周期性来完全解释，而且在采用改进的算法后幂指数依然随着个体的活跃度单调增加，这说明每个人内在的活跃性会影响幂指数的大小，时间间隔的幂律分布是由人的包括总体活跃性在内的内禀特性决定的。

5 结束语

文中结合两种时间重定标算法，综合考虑活跃度的周期与波动和个体内在活跃性的影响，兼顾了两者的优点。将改进后的算法在AOL和Delicious数据集上做了实验。实验结果表明人类行为时间间隔之所以服从幂律分布，与活跃度的周期性和波动无关，而是由人内在特性决定的，并且幂指数随个体活跃性单调增加。

每个人都与其他人不同，但是人的内在特性在时间间隔分布上却统一体现出幂律特性，这是今后要考虑的问题，有学者将幂律在数学上的描述即分形与混沌理论结合起来，提出幂律分布的产生可能是非线性系统下自组织主导的过程产生的必然结果。对人类行为的深入理解，有助于解释若干复杂的社会经济现象，并在舆情监控、疾病防治、交通规划、呼叫服务、信息推荐等方面产生应用价值。但科学是一把双刃剑，人类动力学的研究也可能会导致个人隐私被侵犯。在文章的最后，特别呼吁相关的科研人员，在专注科学研究的同时，探索保护个人隐私的科学手段，尽量消弭研究带来的负能量。