AGA8方程在天然气物性方面的应用

张明洋

中国石化石油机械股份有限公司 三机分公司（湖北 武汉 430040）

0 引言

1992 年6 月，国际标准化组织(ISO)天然气技术委员会及分析技术分委员会(TC193/SC1)在挪威斯泰万格(Stavanger)召开了第四次全体会议，会上推荐了两个精度较高的计算工作状态下天然气压缩因子的方程，即AGA8-92DC 方程和SGERG-88 方程。至今一直被作为天然气压缩因子计算的国际标准。

ISO 12213-2006“天然气压缩因子的计算”标准包括3个部分，GB/T 17747.1～3—2011《天然气压缩因子的计算》也包括3 个部分：①GB/T 17747.1—2011《天然气压缩因子的计算第1 部分：导论和指南》等效采用ISO 12213-1：2006《天然气压缩因子的计算导论和指南》。②GB/T 17747.2—2011《天然气压缩因子的计算第2 部分：用摩尔组成进行计算》等效采用ISO 12213-2：2006《天然气压缩因子的计算用摩尔组成进行计算》，给出了用已知气体的详细的摩尔组成计算压缩因子的方法，即AGA8—92DC 计算方法。③GB/T 17747.3—2011《天然气压缩因子的计算第3 部分：用物性值进行计算》等效采用ISO 12213-3：2006《天然气压缩因子的计算用物性值进行计算》，给出了用包括可获得的高位发热量(体积基)、相对密度、C02含量和H2含量(若不为零)等非详细的分析数据计算压缩因子的方法，即SGERG-88计算方法。

本 文 以ISO12213-2：2006（即GB/T 17747.2—2011）为基础，对AGA8-92DC(以下简称AGA8)方程进行了一定程度的应用研究，拓展了标准在天然气物性计算方面的应用，效果良好。对AGA8 方程的推广应用具有重要的工程意义。

1 AGA8方程及计算方法简介

1.1 AGA8方程

ISO 12213-2：2006标准给出一个计算工作状态下天然气压缩因子的精度较高AGA8 方程(此方程也见于GB/T 17747.2—2011)；该方程是扩展的维利方程[1-2]，其形式为：

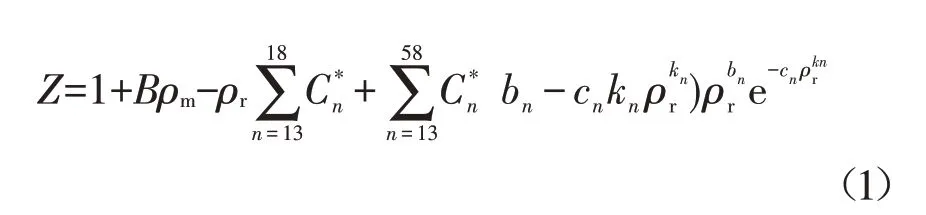
式中：

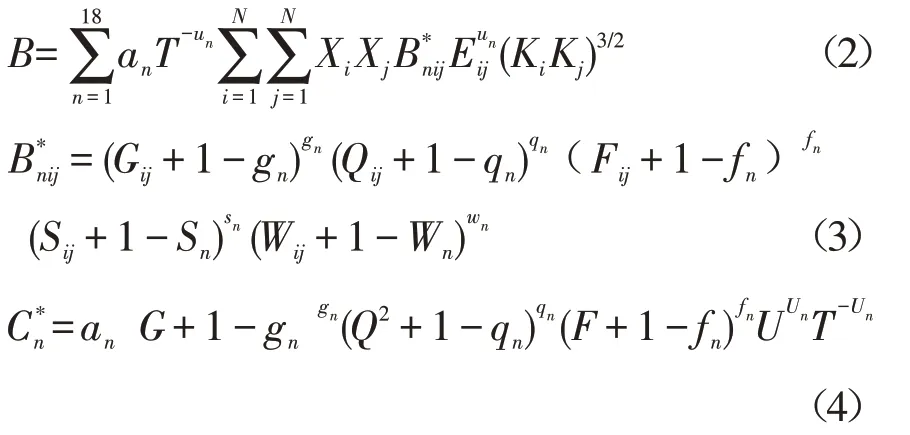
对比密度ρr同摩尔密度ρm相关，两者的关系由式（5）给出：

式中：Si、Sj为组分i、j 的偶极参数；Wi、Wj为组分i，j的组合参数；Qi、Qj为组分i、j的四级参数；Fi、Fj为组分i、j的高温参数；其他参数单位及意义见表1。

后面所述计算方法都是以式(1)—(6)为基础进行的,同时后文中都用ρ 代替ρm。

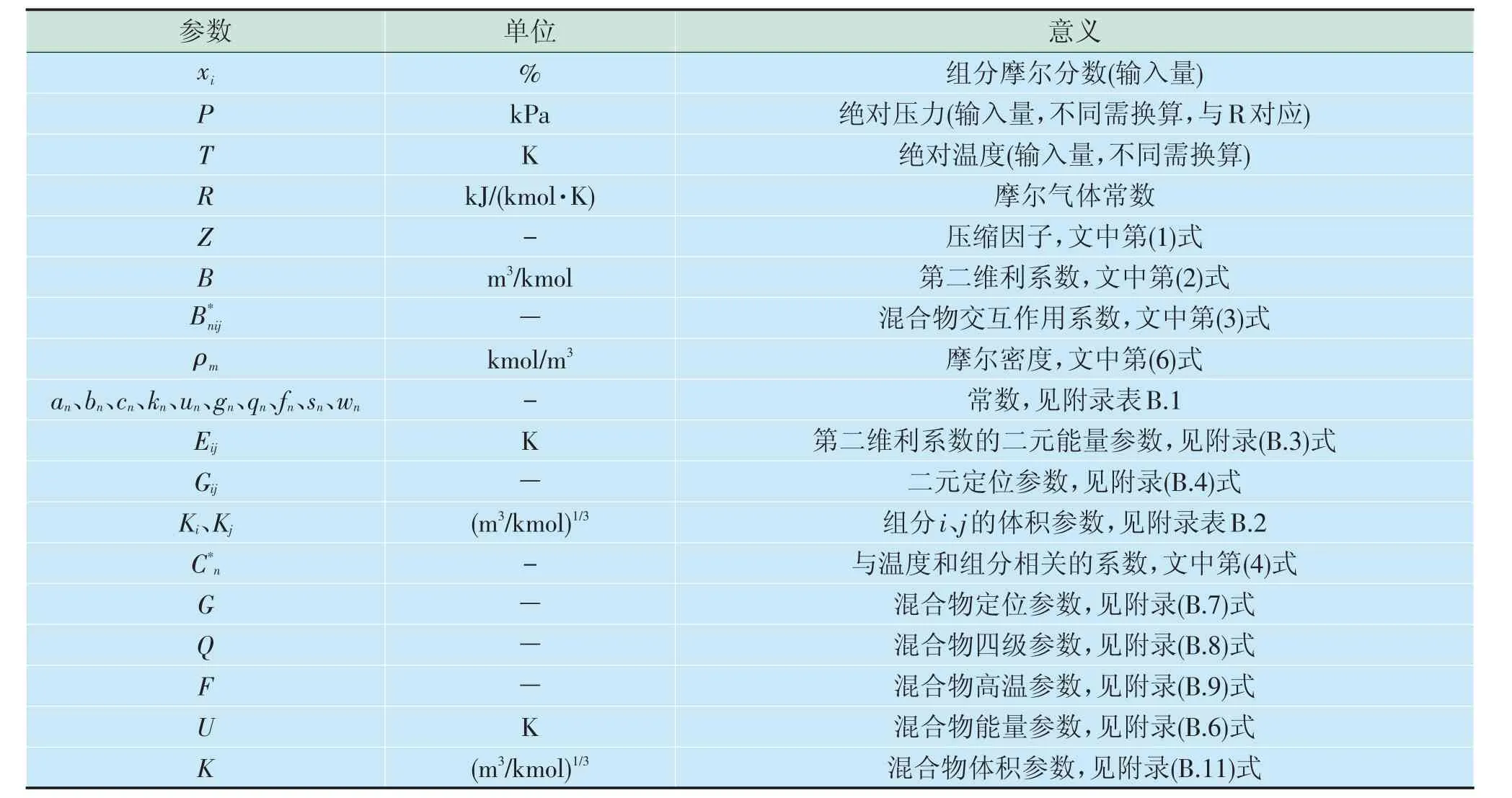
表1 AGA8方程参数单位及意义

1.2 计算方法简介

压缩因子Z的计算方法是ISO 12213-2：2006的基本内容，标准有详细介绍。介绍计算方法如下：首先利用附录B给出的相关数据和表达式计算出B和C*n(n=13~58)。然后通过适当的数值计算方法，求解联立方程式(1)和(6)得到ρ 和Z。

2 AGA8方程的两种形式

AGA8 方程(1)—(6)通过不同的变换，可以得到两种形式的状态方程，将其称为压缩因子Z 形式的Z方程和摩尔密度ρ形式的ρ方程。

2.1 压缩因子Z表示的Z方程

将式（5）、式（6）代入式（1）有：

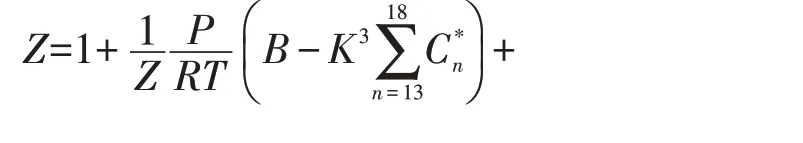
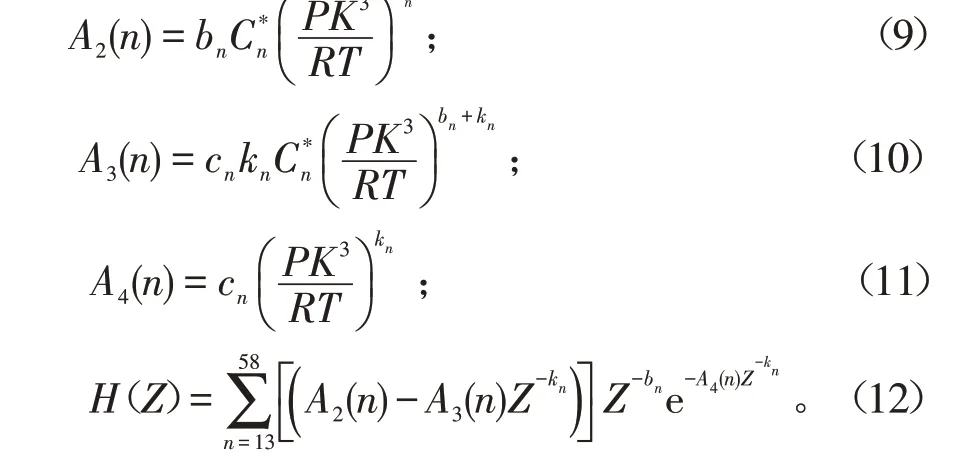
将式（8）、（9）、（10）、（11）、（12）代入式（7），则有：

式(13)即为压缩因子Z形式的Z方程，这是一个超越方程。

2.2 摩尔密度ρ 形式的ρ 方程

将式(1)、式(5)代入式(6)有：

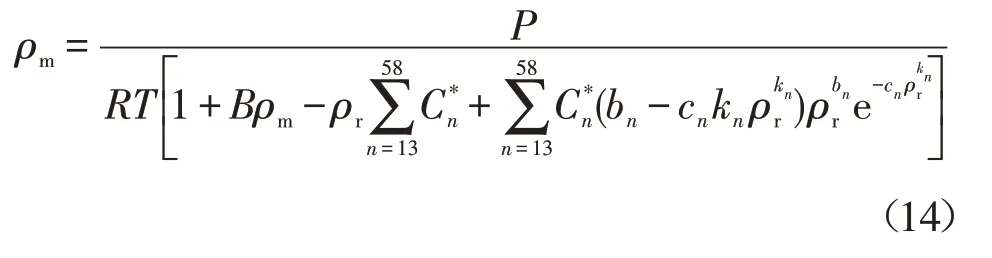
整理式(14)得：

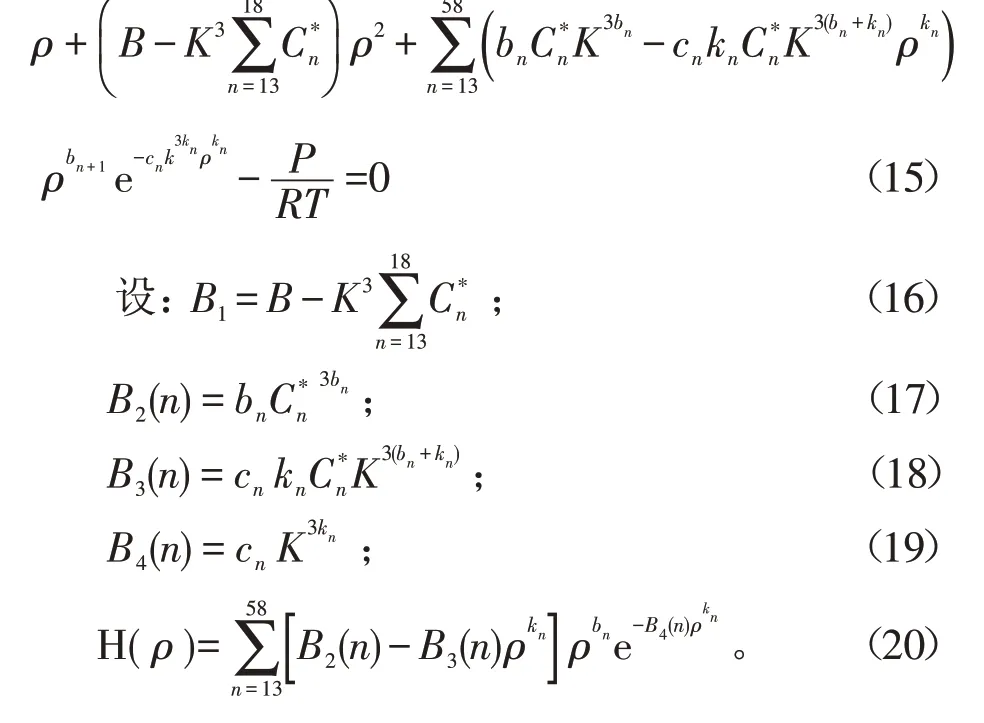
将式（16）、（17）、（18）、（19）、（20）代入式（15），则有：

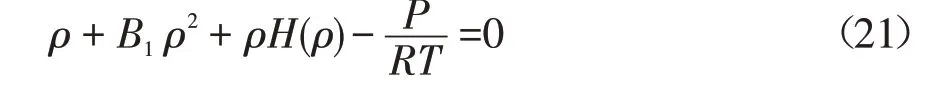
式(21)即为摩尔密度ρ 形式的ρ 方程，这也是一个超越方程。

3 AGA8方程的牛顿迭代法

Z方程式(13)和ρ 方程式(21)，都是超越方程，其求解方法可采用一般迭代法、二分法、割线法和牛顿迭代法来求解。下面给出方程式(13)和式(21)牛顿迭代法。

3.1 Z方程的牛顿迭代法

式（13）的函数式为：

f(Z)的导数为：

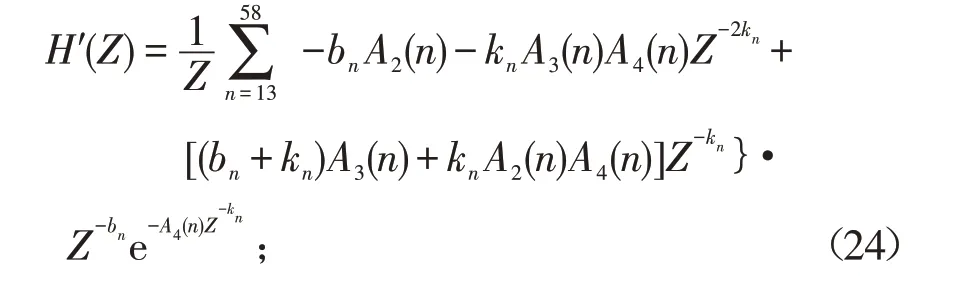
Z方程中式(12)H(Z)的导数

因此，式（13）牛顿迭代式为[5]

根据Z值性质，可选定适当的初值Z0进行求解。

3.2 ρ方程的牛顿迭代法

式(21)的函数式为：

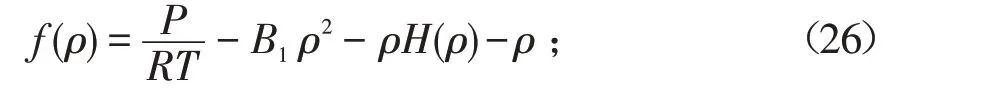
f（ρ）的导数式为：

ρ方程中式(20)的导数：

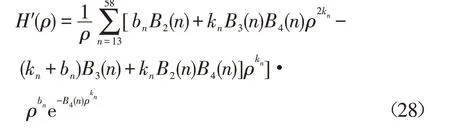
因此，式(21)牛顿迭代式为[5]：

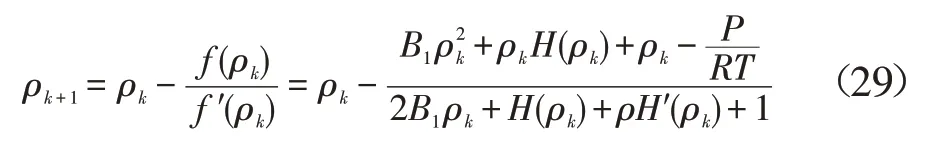
根据Z值性质及Z与ρ的关系，可选定适当的初值ρ0进行求解。

4 AGA8方程偏导数计算

基本状态参数P、v(或ρ)、Z、T 偏导数的计算是AGA8 方程拓展应用的基础，许多气体物性参数都是以基本状态参数偏导数形式来表达。

这里用AGA8的ρ方程来计算AGA8的偏导数，由 (21)可得

4.1 第一个基本偏导数

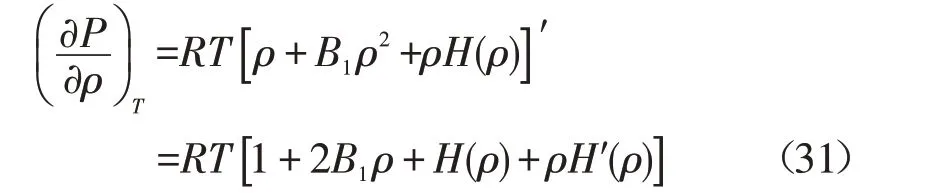
代入式(20)、式(28)，式(31)可化为：

4.2 第二个基本偏导数

式(30)ρ 不变，对T 求导，可得第二个基本偏导数：

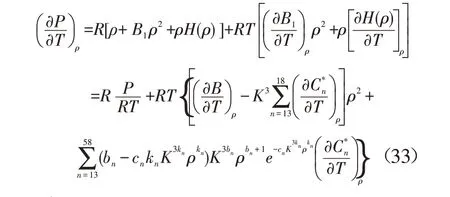
可求出

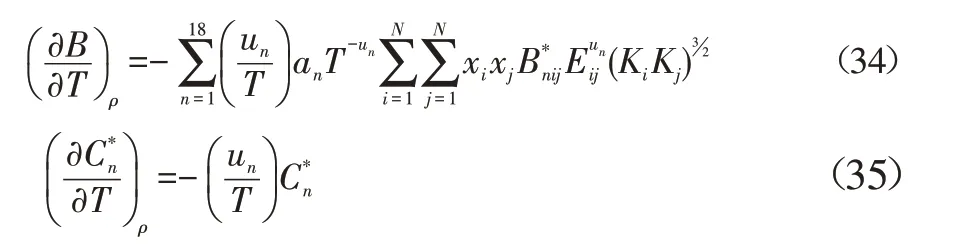
由此可得

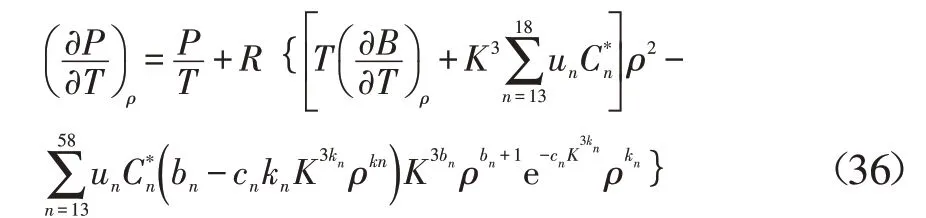
利用式(17)—式(19)，则式(36)可以改写为：

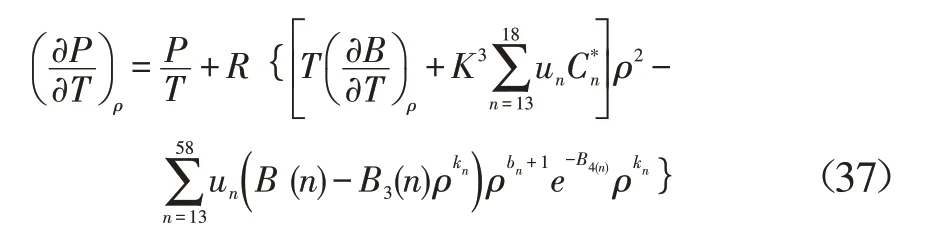
4.3 基本状态参数的其他偏导数

有了上述两个基本偏导数，就解决了其他基本状态参数偏导数计算。如

5 AGA8方程的应用

5.1 AGA8方程计算导数压缩因子ZT

导数压缩因子ZT的定义为[6]：

根据定义，导数压缩因子ZT计算式为：

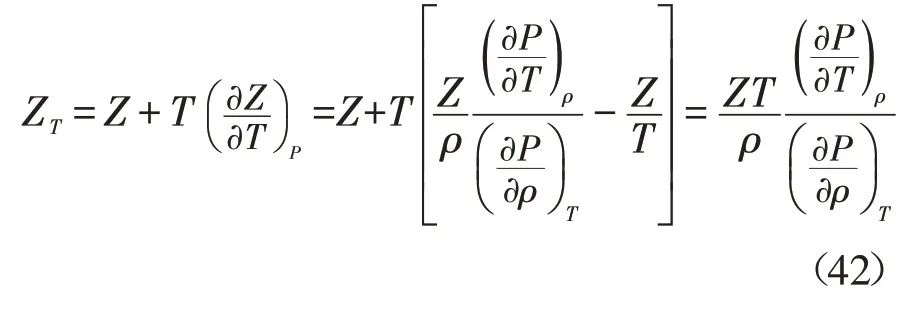
5.2 AGA8方程计算导数压缩因子ZP

导数压缩因子ZP的定义为[6]：

根据定义，导数压缩因子ZP计算式为：

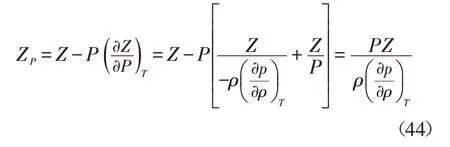
式(42)、式(44)即为AGA8 方程计算导数压缩因子的表达式。两式结合定压热容CP及定容热容Cv，还可以计算出天然气的温度绝热指数kT及容积绝热指数kv。

5.3 AGA8方程计算焦耳汤姆逊系数

焦耳汤姆逊系数定义为[3-4]：

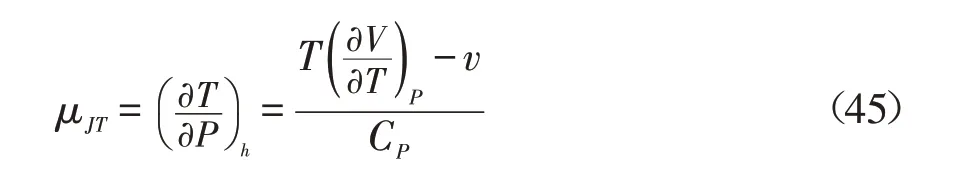
因此，焦耳汤姆逊系数计算式为：

式（46）结合定压热容CP即为AGA8 方程计算焦耳汤姆逊系数表达式。

5.4 AGA8方程计算比热容差

比热容差的表达式为[3]：

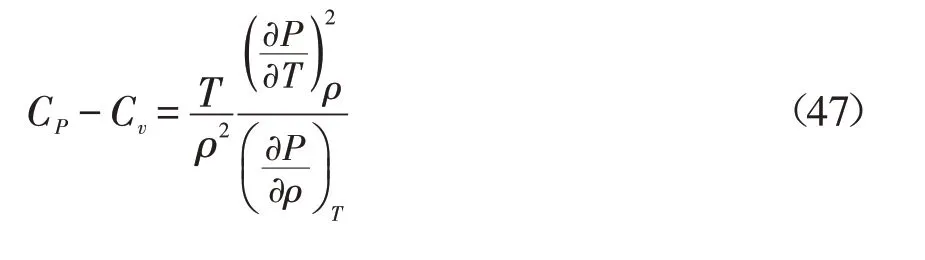
式（47）即为AGA8方程计算比热容差的表达式。

5.5 AGA8方程计算热系数

《工程热力学》中，定义了几个热系数[3]，它们是定温压缩系数，热膨胀系数和弹性系数。

5.5.1 定温压缩系数

定温压缩系数(也称等温压缩率)是指在定温过程中，比体积随压力的变化率与该状态下的比体积的比值。

根据定义可得

5.5.2 热膨胀系数

热膨胀系数(也称体积膨胀系数)是指在定压过程中，比体积随温度的变化率与该状态下的比体积的比值。

根据定义可得

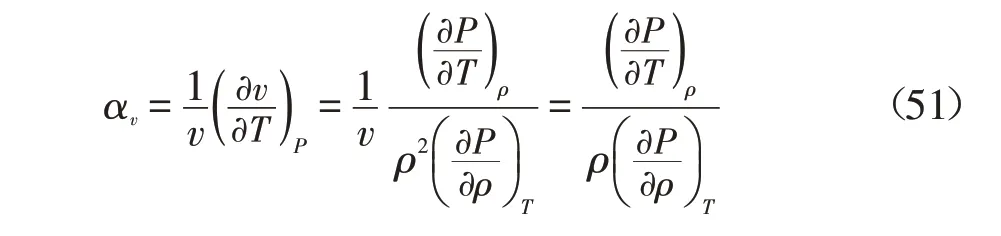
5.5.3 弹性系数

弹性系数(相对压力系数)是指定容过程中，压力随温度的变化率与该状态下的压力的比值。

根据定义可得

其他涉及到状态参数偏导数的天然气物性参数也可以按同样的方式计算。

6 AGA8 和BWRS 方程在天然气物性计算方面的比较

下面以GB/T 17747.2—2011标准中给出的输配条件和6组气样，用AGA8方程和BWRS方程进行了对比计算，标准中只给出6组气样的Z值，对应表3、表4 中GB 17747.2—2011 中Z 值，表中其他数值是扩展计算结果。

1）GB/T 17747.2—2011 附表C中的1#、2#、3#气样物性计算比较见表2。

2）标准GB/T 17747.2—2011附表C中的4#、5#、6#气样物性计算比较见表3。

3）从对比计算可以看出：计算Z 值AGA8 比BWRS 的Z 值相对误差小，与GB 17747.2—2011中Z值相比，AGA8精度更高。

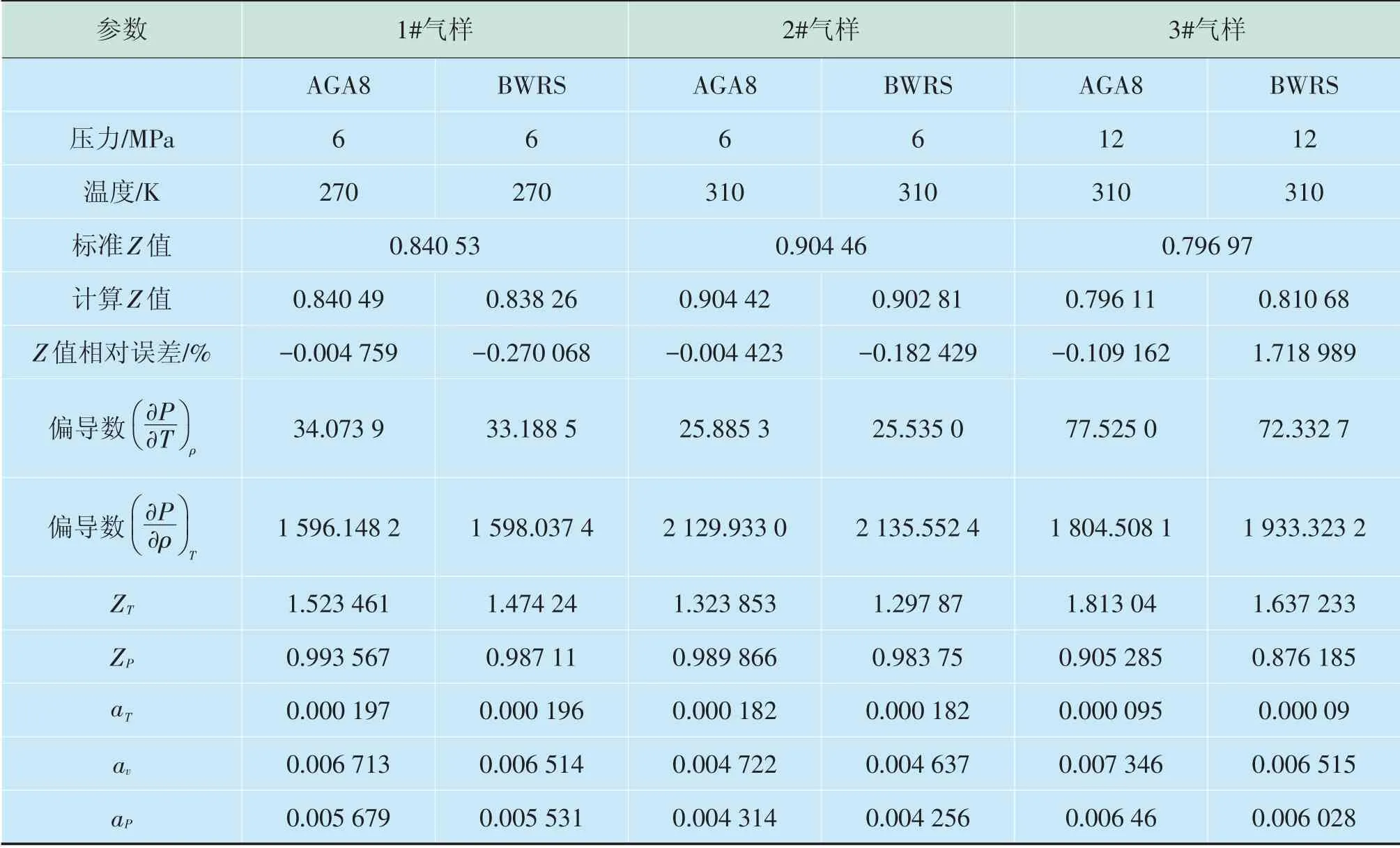
表2 1#、2#、3#气样物性计算比较

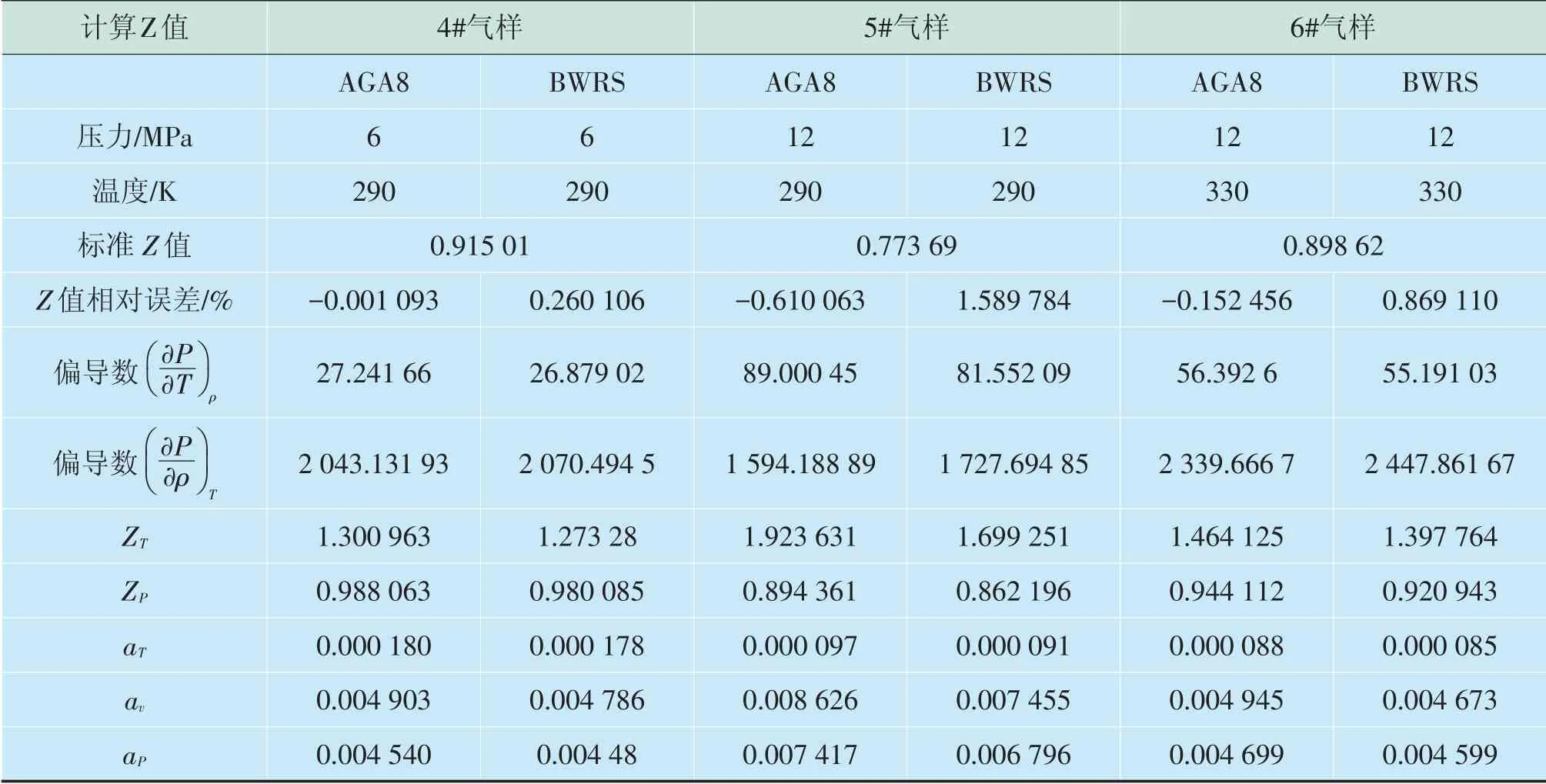
表3 4#、5#、6#气样物性计算比较

4）BWRS 的Z 值 相 对 误 差 较 小 时，AGA8 与BWRS的各种物性值比较接近；BWRS的Z值相对误差较大时，AGA8 与BWRS 的各种物性值相差较大。在相同输配条件下，AGA8方程的Z值及相应摩尔密度ρ 值比BWRS 方程的Z 值及相应摩尔密度ρ值精度更高。这说明，用AGA8 方程计算天然气其他物性参数比BWRS方程更好。

7 结论

1）通过编程用AGA8方程计算出的压缩因子Z值与GB/T 17747.2—2011标准计算出的Z值相对误差通常小于1%，与标准中给出的对比Z系数十分接近，其计算结果，可以运用到实际的工程计算中。

3）结合定压热容Cp及定容热容Cγ后，可以计算出天然气比热比、温度绝热指数、容积绝热指数、焦耳汤姆逊系数等物性参数，进一步拓展AGA8 方程的应用范围。