一种井眼轨迹不确定性方法的可视化研究与应用

龚大洪， 陈元鹏， 杨文娟， 杨金生， 王志玲， 张树义， 马鸿彦

(1中国石油集团渤海钻探工程有限公司定向井技术服务分公司 2中国石油渤海钻探工程技术研究院 3中国石油集团渤海钻探工程有限公司第五钻井工程分公司 )

在钻井过程中井眼轨迹的延伸是一个动态的过程，如果想实时监控井眼轨迹并且对其有个更直观的认识，则在实现井眼轨迹三维可视化的基础上通过合理的误差模型进一步实现三维井眼轨迹误差椭球可视化对丛式井井眼防碰或救援定向井连通等具有很好的指导意义[1-7]。

目前，运用最为广泛的井眼轨迹不确定性误差描述模型有系统误差模型和ISCWSA误差模型。系统误差模型为Wollf[8]和 Wardt于1981年提出的井眼轨迹不确定性分析模型 ，简称WdW模型，该模型只提出了六个误差源，更适用于研究基于陀螺类测斜工具测量垂直井和中等斜度井时系统误差引起的井眼位置不确定性，具有一定的局限性。ISCWSA误差模型为井眼测量精度工业导向委员会通过的一种误差模型，它以Williamson[9]于2000年提出的基于磁性仪器的误差分析模型为基础并且还在不断的完善，该模型提供了井眼轨迹不确定性分析的数学框架，能综合考虑系统误差、随机误差和全局误差，被广泛应用到石油行业中。

一、 ISCWSA误差模型及测量误差源分析

1. ISCWSA模型

磁性测量工具测量的井眼轨迹受到很多误差项的影响，这些误差项可以归集为几个大的误差源且这些误差源是相互独立的，ISCWSA模型假设误差源在数理统计上服从正态分布，那么在磁性测量工具测量的井眼轨迹上的每个测点的误差源确定该点的其中一个误差。将误差与井眼轨迹三维空间位置相结合，就能用向量把误差表达出来。井眼轨迹上连续两个测点的位置向量用计算位移来表示，定义磁性测量工具测量的井眼轨迹上第k-1个测点和第k个测点之间的位置增量为Δrk，则第l个测段的第k个测点上(观察点以上的测点)由第i个误差源引起的误差为：

(1)

式中:ei,l,k—第i个误差在第l个测段第k个测点NEV轴导致的位置矢量标准差；σi，l—第l组测量第i个误差源的标准差;pk—第k个测点上的测量矢量,p=[DIA]T；∂p/∂εi—第i个误差对测量矢量的影响(一个3×1向量)，即误差的权重函数；dr/dp—测量向量p对要求点井眼位置矢量(NEV轴)r的影响(一个3×3矩阵)。

属于第L个测段的观察点K处第i个误差源引起的误差为：

(2)

2. 测量误差源分析

井眼误差大致可以分为三种类型：系统误差、随机误差和全局误差。

2.1 系统误差及其对应权重函数

在测量井眼轨迹的过程中系统误差又可以再次划分为已定系统误差和未定系统误差。已定系统误差的方向、大小是已知的。未定系统误差由于其方向未知，大小也未知，所以一般情况下只能计算范围，故已定系统误差可以进行修正，而未定系统误差则不能进行修正。

2.1.1 MWD传感器误差权重函数

MWD共有12个传感器误差源，每个误差源对应一个权重函数向量，可通过对井斜角、方位角求误差源偏导数获得。以X轴重力加速度计的偏移误差和X轴重力加速度计的刻度误差为例，通过偏微分求导，从而得到修正后的权重函数ABIX：

(3)

2.1.2 仪器不居中误差权重函数

仪器不居中误差可以细致的归为底部钻具组合垂曲误差项和径向不对称误差项两类。底部钻具组合垂曲只影响井斜角的测量，其大小与垂直于钻具组合的重力分量成正比，底部钻具组合垂曲误差项的权重函数：

(4)

径向不居中误差项认为在X,Y轴上存在相互独立且固定的径向不对称误差，它们在高边和侧向方向上的分量分别导致井斜角误差和方位角误差为：

(5)

(6)

2.1.3 钻具磁干扰误差权重函数

磁方位角误差项权重函数为:

(7)

轴向磁干扰误差项权重函数为：

(8)

2.1.4 深度刻度系数误差权重函数

刻度误差权重函数为：

(9)

2.2 随机误差及其对应权重函数

随机误差通过多次测量估算平均值，这个平均值又称为随机误差限。参考误差权重函数为：

(10)

2.3 全局误差及其权重函数

磁偏角固定数值误差项权重函数：

(11)

磁偏角水平磁场强度(变值)误差项权重函数为：

(12)

磁倾角误差项权重函数为：

(13)

总磁场强度误差项权重函数为：

(14)

拉伸类型误差项权重函数为：

(15)

二、井眼轨迹不确定性误差椭球的计算

在每个误差项权重函数已经被建立的基础上，就能够用向量的形式将每个误差项所产生的误差表示出来，然后根据概率统计相关知识建立协方差矩阵并得出误差椭球来表达井眼位置的不确定性。

将随机误差、系统误差、全局误差三种误差类型相加，就能算出井眼轨迹上任何测点的总的位置不确定性的协方差矩阵为：

(16)

三、误差椭球的三维可视化

用Python语言对ISCWSA误差模型进行描述。根据以上推导公式，把ISCWSA误差模型转化为算法并实现在计算机上，井眼轨迹计算采用最小曲率法。整个程序采用模块化面向对象编程模式，程序的灵活性和可重复利用性强，如图1。

图1 ISCWSA求井眼轨迹不确定性算法流程

由于误差椭球半轴相对于井深来说太小，为了能直观的在三维空间下显示误差椭球，在误差椭球三维可视化的过程中一般需要把椭球半轴长度按照比例放大，放大比例可以根据实际情况而定。针对某一个点的和针对连续多个点的误差椭球可视化图形如图2和图3所示。

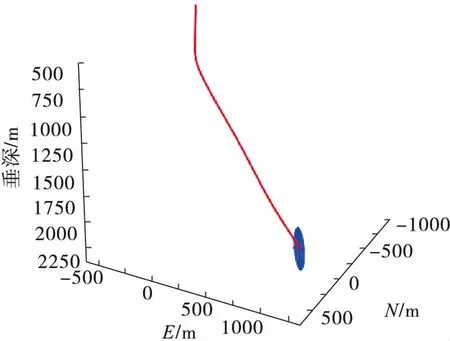
图2 单点误差椭球

图3 连续误差椭球

四、应用实例

目前，MWD随钻测量工具在钻井中的普遍使用，基于ISCWSA模型的井眼轨迹不确定性误差椭球计算和三维可视化对现场钻井施工有着很好的指导作用。例如：为了防止正钻井与邻井相碰，钻井人员可以通过观察钻头所在位置的误差范围是否与邻井交碰来调整钻进方向；在打救援井时为了尽量让其与事故井相碰，钻井人员可以通过井眼轨迹控制来使误差椭球中心靠近事故井，从而最大概率的使救援井与事故井相碰。

为验证实现方法的可行性，选择渤海某平台上的两口相邻的井B1井和B2井来绘制误差椭球，用来验证三维误差椭球可视化在防碰预测和井眼轨迹控制领域的指导意义，两口井的井口间距为25 m，各种计算参数选取文献[4]中提供的参数，井眼轨迹分段数据及相应误差分析结果分别如表1和表2所示。

表1 B1井井眼轨迹分段数据及误差分析结果

表2 B2井井眼轨迹分段数据及误差分析结果

图4 两口井防碰预警或连通示例图

如图4所示，将B2井作为参考井，B1井在钻井过程中，在约2 600 m处误差椭球即将与B2井相碰，若B1井继续按照原来的方向钻进，则与B2井碰撞的概率增大，为防止两井相碰，应及时调整B1井井斜或方位来调整其钻进方向。

五、结束语

该研究用Python编程语言实现了井眼轨迹的三维可视化和基于ISCWSA法误差椭球的计算，并展示了随井深变化的参数信息，取得了良好的效果。在此基础上，利用NumPy, SciPy, Matplotlib,和Axes 3D等函数库实现了对三维空间井眼轨迹误差椭球的可视化，可以直观的显示井眼轨迹上各个测点的误差范围，对丛式井井眼防碰或井眼轨迹控制领域起到了较好的参考和指导意义。