强震作用下软岩隧道洞口段动力响应规律分析
刘博清,赵 杰,王桂萱,兰雯峻
(大连大学 土木工程技术研究与开发中心, 辽宁 大连 116622)
随着我国经济建设的全面发展,许多大型基础工程已列入国家发展规划,其中隧道工程的建设问题是必须面临的一个问题。许多大型基础设施跨越距离大,建设困难,往往都是穿梭在深山峡谷、江流湖泊,工程所处地质复杂,受大自然影响极大。隧道在地震发生的时候往往都会发生某种程度上的破坏,尤其是一些山岭隧道,一旦遭到大地震的破坏,会造很大的损失。山岭隧道洞口作为山岭隧道的重要组成部分,也是最容易出现损坏的地方,一旦遭到地震的破坏,隧道洞口将会堵塞。根据人们对山岭隧道在地震作用下的破坏情况调查研究资料来看,山岭隧道洞口处不仅发生的震害频率高,而且其破坏程度也比其他地方严重,是整个山岭隧道抗震的薄弱环节[1-5]。在地震动作用下,开展软岩隧道洞口段动力响应分析研究具有重要意义。
2008年,王正松等[6]用FLAC3D软件对某隧道洞口段进性数值模拟分析,得出隧道洞口段处的内力峰值最大,采取减震防护措施会取得明显的效果。同样在2008年,蒋树屏等[7]建立某隧道洞口段三维有限元模型,分析出在施加地震荷载后,隧道洞口段衬砌响应时间并不是和地震波的输入时间同步的,并且衬砌在地震荷载作用下以水平向振动为主的,竖向振动相对于较小。21世纪初,高峰等[8]、耿萍等[9]和索然绪等[10]进行三维隧道洞口段抗震研究分析,得出隧道洞口段的围岩类型以及性质对隧道抗震设防的布置影响非常大。2011年,孙铁成等[11]用FLAC3D软件对双洞错距隧道洞口段进行仿真分析,得出在地震荷载作用下,隧道洞口段衬砌横断面的应力、加速度峰值等在地震不同方向的激励下差别很大,而且左右两个洞的洞口段的响应也明显不一样。2013年,曹小平[12]以某隧道洞口段为工程背景,考虑隧道围岩的弹塑性特点、运用动力有限元原理,分析出隧道洞口段在强震作用下最不利的地震传播方向,同时分析了在强震作用下,隧道洞口段衬砌与隧道埋深的动力响应规律。2014年,赵杰等[13]开展了核电取水隧洞洞口段抗震稳定分析。2015年,赵成林[14]通过对隧道震害统计表明,隧道洞口段是隧道抗震的薄弱环节。2016年,孙纬宇[15]研究分析了在地震作用下,不同坡度和坡高对隧道洞口段的动力响应规律。2017年,李云刚[16]用有限差分软件FLAC3D对隧道施工工法进行数值分析得出有关沉降和底部回弹量的基本规律。韩吉珅等[17]定量的分析了对隧道软弱围岩进行预加固可以有效的改善围岩失稳。2018年,王朝凤[18]对不同埋深的隧道进行数值模拟分析,得出了软岩隧道洞口段处的加速度、位移、弯矩、轴力的相关规律。尽管现在许多学者的研究分析结果对隧道洞口段的抗震有一定的价值,但是考虑的因素还不够全面,很多研究结论并不是完全一致。因此有必要对岩体隧道洞口段的地震特性做进一步的深入研究。
本文建立隧道洞口段三维有限元模型,运用有限元差分方法对隧道洞口段进行动力响应分析,通过隧道拱顶、拱腰、拱脚五个监测点研究隧道洞口段最大加速度和最大水平位移的变化情况,得到在软岩不同弹性模量、泊松比、坡度以及双隧道不同间距条件下隧道洞口段动力特征响应规律和塑性区分布变化情况。
1 动力响应分析方法
1.1 动力边界选取
动力计算时人工边界的精度对连续介质材料数值计算的准确性产生较大影响。我们将边界分成静力人工边界与动力人工边界两类,其中地震波以应力或加速度时程的形式施加到黏弹性边界上,如图1所示。
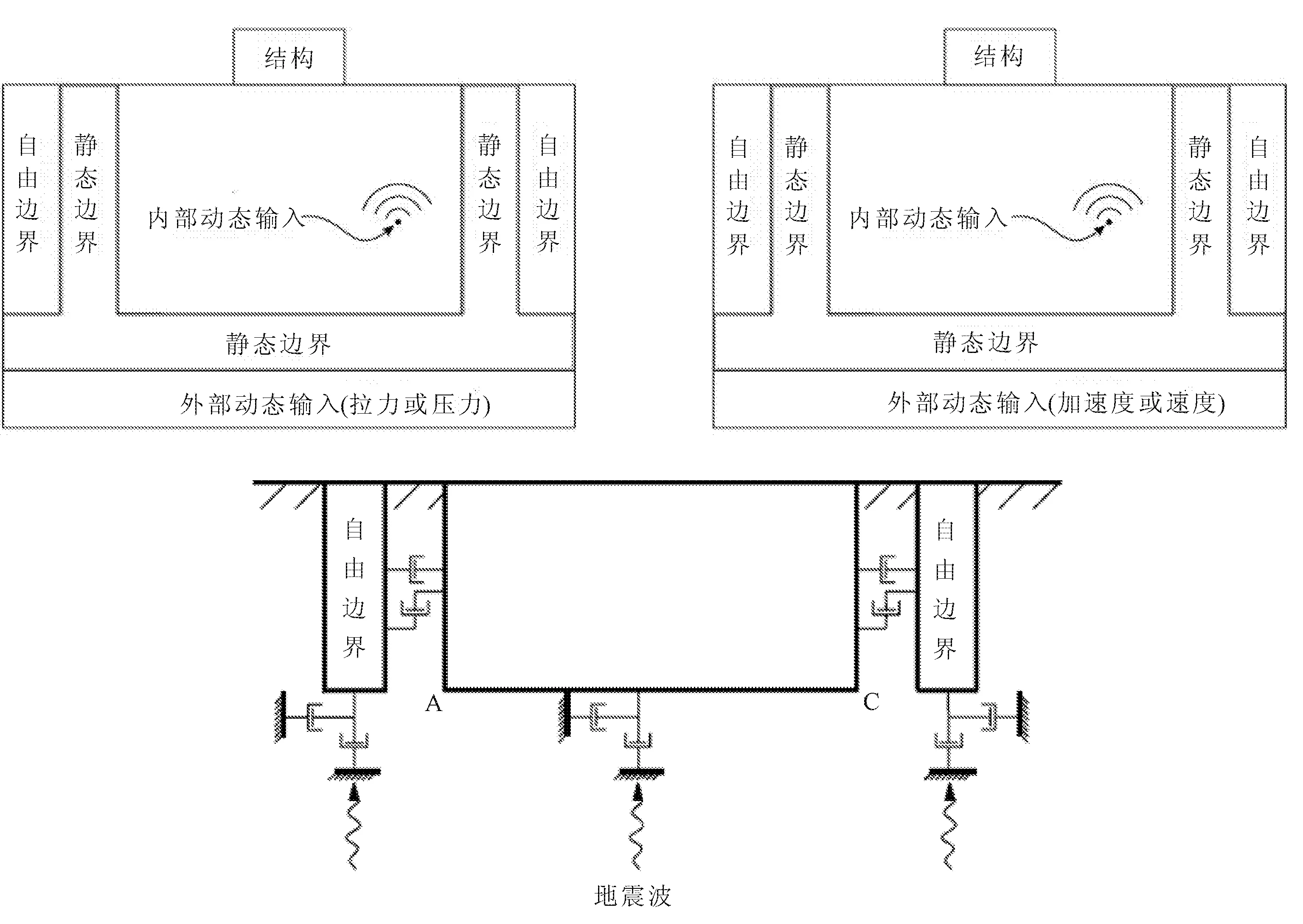
图1 FLAC3D动力加载及边界约束模式
黏性边界最早是由Lysmer和Kuhlemeyer在1969年提出,是通过在边界上施加正向和切向并且与边界无关的黏壶,来提供正向和切向黏性阻力(tn,ts):
tn=-ρCpvn;ts=-ρCsvs
其中:vs,vn分别是边界速度的正向分量及切向分量,ρ为对应各层结构土体的介质密度,Cp为P波在介质中传播速度,Cs为S波在介质中的传播速度。
计算模型中要准确模拟地震波的传播过程必须要求空间网格尺寸Δl在输入最高频率波长的1/10~1/8之间,即:
Δl<λ/10
1.2 阻尼的选取
阻尼是结构的动力特性之一,瑞利阻尼的假设条件是结构的阻尼矩阵是质量矩阵和刚度矩阵的线性组合,即:
[C]=α[M]+β[K]
(1)
式中:α为质量阻尼系数;β为刚度阻尼系数。在进行结构动力计算时,一般各阶振型都用相同的阻尼比。这样两个阻尼系数就可以通过阵型阻尼比计算获得,即:
(2)
(3)
式中:ωi和ωj分别为结构的第i阶和第j阶固有频率;ξi和ξj为相应于i和j阵型的阻尼比,由实验确定。一般情况取i=1,j=2,相应阻尼比在2%~5%范围内选取。
1.3 地震动输入
在地震荷载作用下对结构的稳定性分析是FLAC3D动力计算的关键内容。FLAC3D中包含加速度时程、速度时程、应力时程和集中力时程4种可输入的动力荷载。地震荷载可以结合Fish语言写入到FLAC3D动力计算文件来施加到模型底面上。其中动力荷载的边界条件需要进行以下选择:
(1) 刚性地基。当模型最底部的材料为弹性模量较大岩石时,可直接采用自由场边界条件将加速度或速度荷载直接输入到模型底面,进行计算。
(2) 柔性地基。当模型底部材料的弹模参数较小时,模型周围采用自由场边界条件,模型底部可采用静态边界条件。
FLAC3D采用完全非线性的动力分析方法,动力分析过程见图2。

图2 FLAC3D完全非线性动力耦合求解流程图
1.4 本构模型
岩土工程应用中,摩尔-库仑本构模型是最为常用的模型,计算速度较快,是在摩尔-库仑准则(见图3)的基础上的组合屈服本构关系。σ1、σ2以及σ3为该模型的三个主应力,其大小关系可以表位为:σ1≤σ2≤σ3,并用σ1σ3定义屈服准则,其中σ1σ3是建立在由σ1σ3构成的应力平面内的,假设三个主应力受拉为正,为压应力时为负,用函数f(σ1,σ3)=0表示其破坏包络线,如图4所示。

图3 摩尔-库仑在主应力空间的屈服面
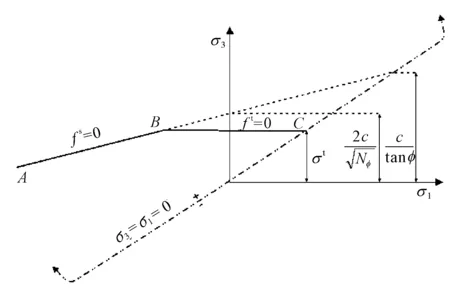
图4 FLAC3D中的摩尔-库仑屈服准则
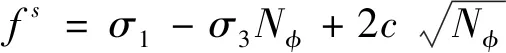
可以用函数gs和函数gt来描述屈服势函数,gs采用非相关的流动法则:
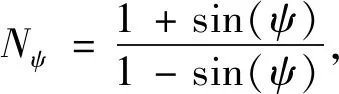
gt采用相关的流动法则,gt=-σ3,表示拉伸塑性流动。流动法则的定义形式如图5所示。
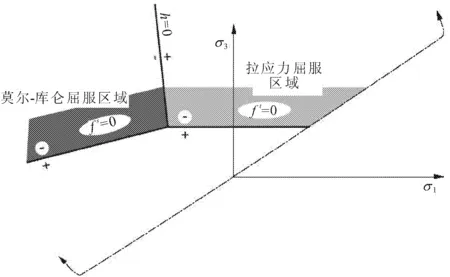
图5 摩尔-库仑屈服准则及其屈服定义
fs=0和ft=0屈服区域的公共线可以用函数h(σ1,σ3)=0来定义,
h=σ3-σt+ap(σ1-σp)

从函数h=σ3-σt+ap(σ1-σp)的计算结果可以确定材料是拉伸破坏还是压缩破坏,计算结果h若是大于零,则表示破坏为拉伸破坏,势函数方程式为:gt=-σ3;若计算结果h小于零,则表示材料所受破坏为剪切破坏,此时的是函数为:gs=σ1-σ3Nψ。
2 强震作用下三维隧道洞口段动力响应分析
2.1 隧道动力计算模型的建立
隧道洞口段的地震响应有许多影响因素,现在主要讨论隧道洞口段结构在软岩不同弹性模量、泊松比以及坡高的情况下地震动响应分析及塑性区分布规律研究,故将该隧道简化为一种均质材料。首先利用ANSYS建立一个长为100 m,宽为75 m,高为60 m,坡角为45°的隧道洞口段模型,讨论软岩弹性模量和泊松比对隧道洞口段结构在地震动下的响应规律;然后建立坡角为30°、40°、50°、60°的4个数值计算模型用来讨论坡角对隧道洞口段结构在地震动下的响应规律。以上模型的洞径均为10 m,隧道洞口断面见图6,每个模型均在洞口段取左拱脚、右拱脚、左拱腰、右拱腰、拱顶五个监测点,如图7所示,左右围岩取3倍洞径,隧道底部向下延伸40 m。在FLAC3D中的计算模型图如图8所示。

图6 隧道洞口断面图(单位:mm)
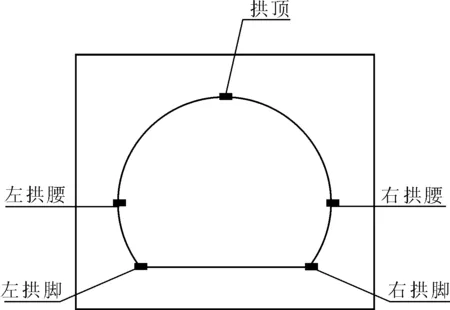
图7 监测点分布图
将建立好的ANSYS模型导入到有限差分软件FLAC3D中,模型四周加自由场边界,底部施加黏性边界。查软岩相关资料,取软岩弹性模量取值范围为2 GPa到5 GPa,泊松比范围是0.32~0.38,具体软岩材料力学参数如表1所示。
图8 计算模型

表1 材料力学参数
模型从ANSYS软件中导入到FLAC3D中后,首先给模型施加合理的边界,每次输入两个方向的水平地震波和一个方向的竖直地震波,其中水平地震波1为隧道模型长度方向,水平地震波2为隧道模型宽度方向,竖直地震3为隧道高度方向,振幅峰值都为0.1g,持续时间为30 s,为RG1.60时程地震波,具体地震波时程曲线如9所示。
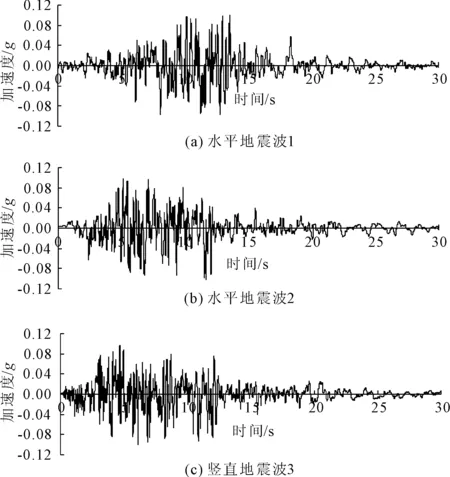
图9 RG1.60的地震波时程曲线
2.2 软岩弹性模量对动力响应规律的影响
分析讨论软岩弹性模量对隧道洞口段的塑性区分布、加速度和位移在地震作用下的响应规律。
动力响应规律:
图10、图11分别给出了隧道洞口段位移峰值和加速度峰值随软岩弹性模量变化关系图。
软岩在地震动作用下将会发生很明显的塑性变化,在洞口处及其上方尤为明显,其中在坡度转角处出现了塑性区贯通现象,表明隧道容易在转角处达到屈服状态,其中当E=2 GPa时,其塑性区体积为9 065.5 m3,当E=3 GPa时,其塑性区体积为8 857.9 m3,当E=4 GPa时,其塑性区体积为8 368.9 m3,当E=3 GPa时,其塑性区体积为5 355.2 m3,总体上塑性区分布范围随着软岩的弹性模量的增大而逐渐减小。

图10 隧道监测点段加速度峰值随软岩弹性模量变化关系图
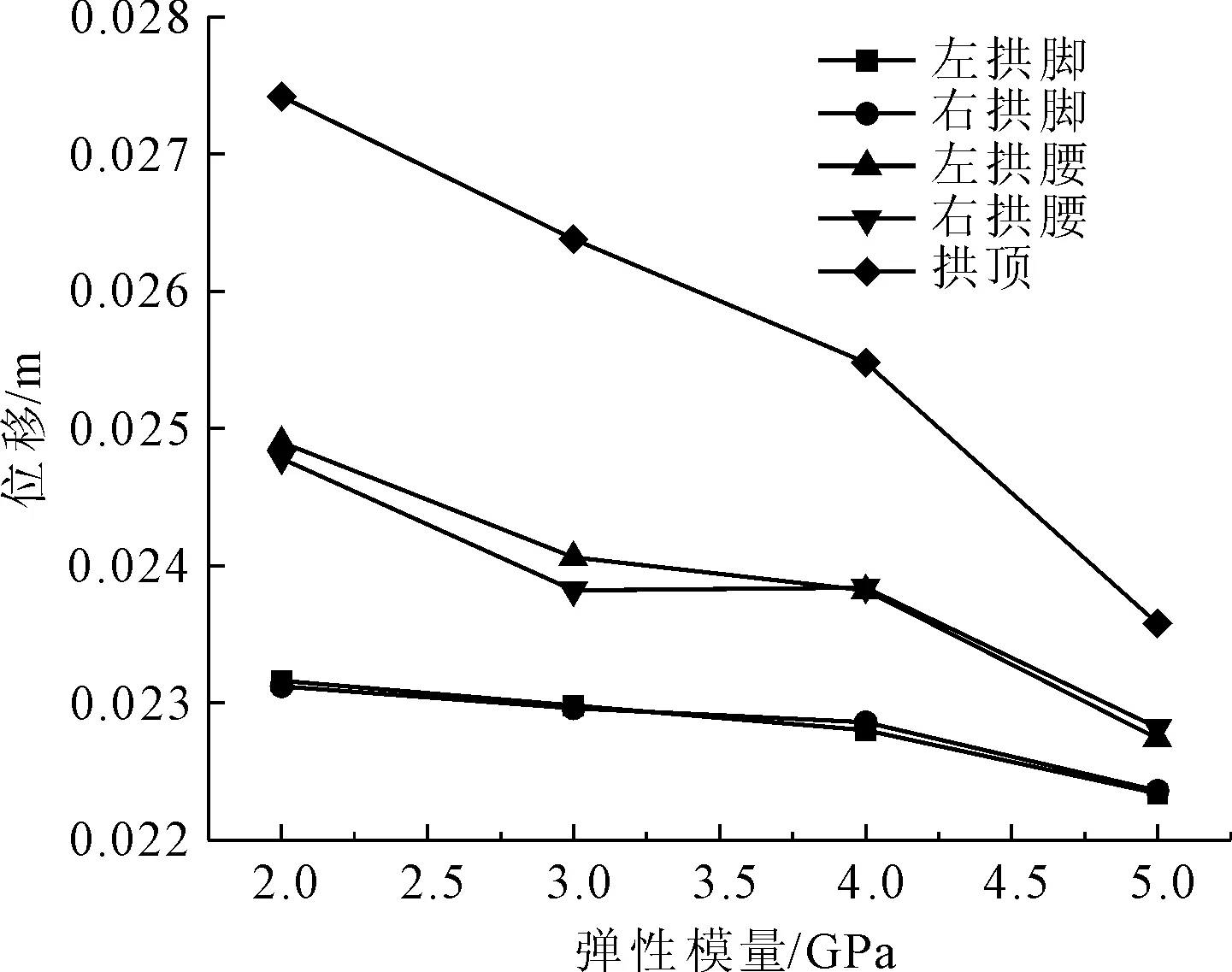
图11 隧道监测点段位移峰值随软岩弹性模量变化关系图
从图10可以看出,在地震作用下,隧道洞口段监测点的最大加速度随着弹性模量在适当的范围内的增加而先增加后减小,并且随着隧道洞口段监测点的高程的增加而逐渐递增,拱顶的加速度峰值明显大于拱腰处的加速度峰值,拱腰处的加速度峰值要大于拱脚处的加速度峰值,而拱脚与拱腰之间的加速度峰值差别不大。从图11可以看出,监测点的位移峰值随着软岩弹性模量的增加而逐步递减,且高程越大递减得越快。
2.3 软岩泊松比对动力响应规律的影响
分析讨论软岩泊松比对隧道洞口段的塑性区分布、加速度和位移在地震作用下的响应规律。
动力响应规律:
图12、图13分别给出了隧道洞口段位移峰值和加速度峰值随软岩泊松比变化关系图。
软岩在地震动作用下将会发生很明显的塑性变化,在洞口处及其上方尤为明显,但是在软岩的泊松比发生改变的情况下,塑性区不会发生大的变化,当μ=0.32时,塑性区体积为9 774.4 m3,当μ=0.34时,塑性区体积为9 384.8 m3,当μ=0.36时,塑性区体积为8 566.2 m3,当μ=0.38时,塑性区体积为7 259.1 m3,总体上是随着软岩泊松比的增大塑性区而略微的有减小的趋势。
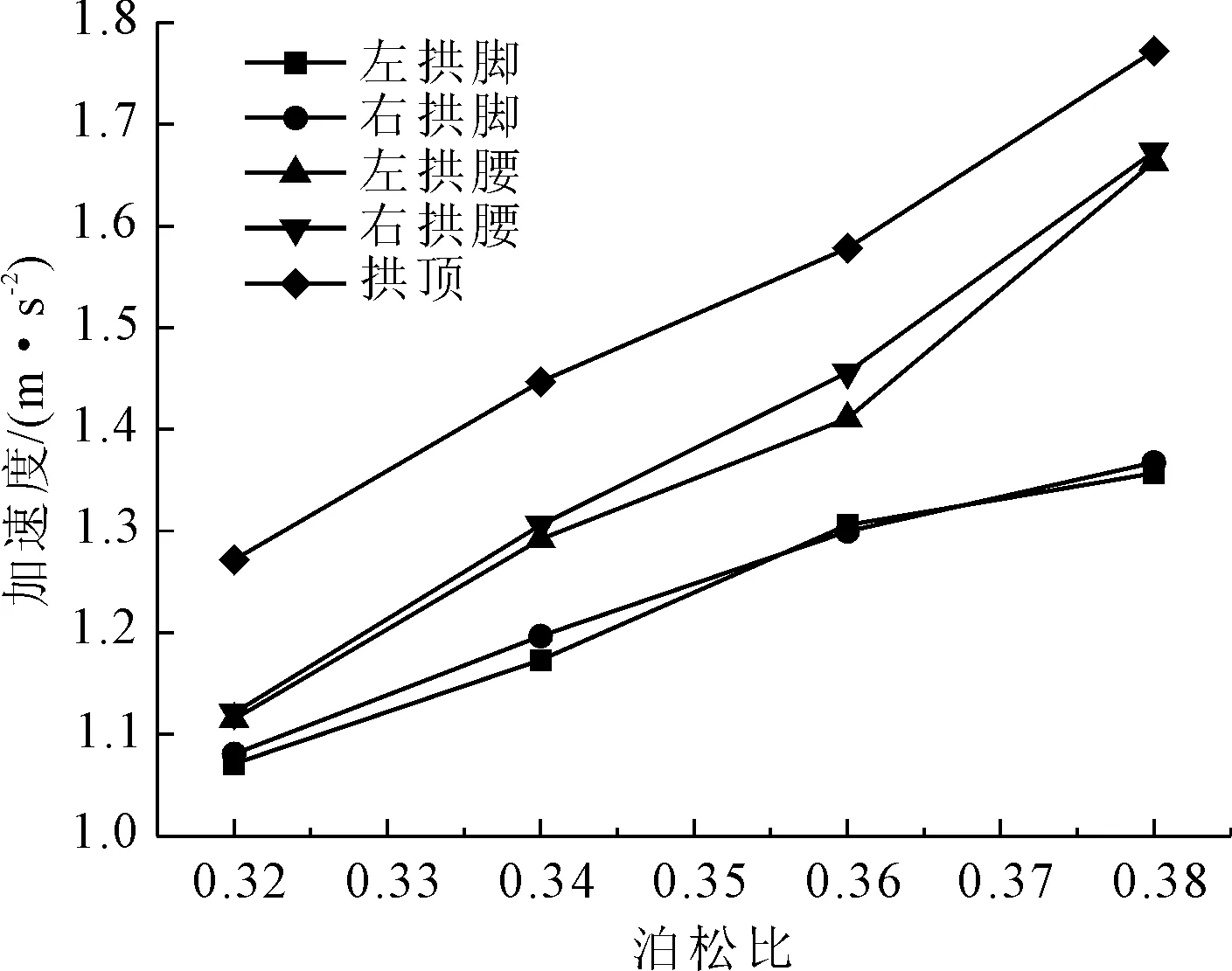
图12 隧道监测点加速度峰值随软岩泊松比变化关系图

图13 隧道监测点位移峰值随软岩泊松比变化关系图
图12、图13表明,在地震作用下,隧道洞口段监测点的加速度峰值随着软岩泊松比的增加明显变大,同时随着监测点高程的增加而增加;然而,位移峰值随着泊松比的增大变化不大。只是缓慢的递减,而随着高程的增加具有明显的变大趋势。
2.4 坡角对动力响应规律的影响
分析讨论隧道洞口段边坡的陡峭对隧道洞口段的塑性区分布、加速度和位移在地震作用下的响应规律。
动力响应规律:
图14、图15分别给出了隧道洞口段位移峰值和加速度峰值随隧道坡度变化关系图。
虽然软岩在地震动的作用下发生了明显的塑性,但是先是发生在洞口附近,尤其是在坡脚与路面相接触的地方最先开始出现了贯通的塑性区,然后向四周扩散。当坡角为30°时,塑性区体积为5 956.7 m3,当坡角为40°时,塑性区体积为7 792 m3,当坡角为50°时,塑性区体积为9 433 m3,当坡角为60°时,塑性区体积为11 460 m3,随着坡度的增加塑性区分布明显的增大。说明坡度越陡峭,隧道在地震荷载的作用下就越容易发生破坏,必要时应该采取加固防范措施。
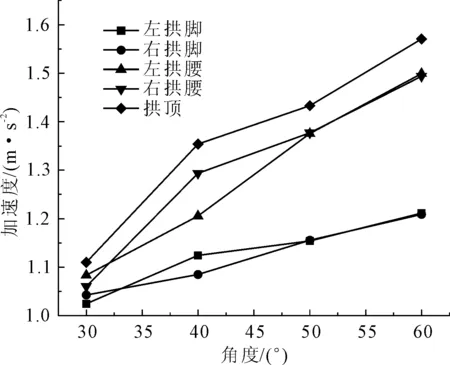
图14 隧道监测点加速度峰值随坡度变化关系图

图15 隧道监测点加速度峰值随坡度变化关系图
从图14和15可以看出,在地震作用下,隧道洞口段的监测点的加速度峰值和位移峰值都是随着坡度角度的增大而逐渐增大,但是位移加速度峰值相对于加速度峰值增加得缓慢一下,并且高程越大,加速度峰值越大。可以看出,在建立地下结构时,在允许的范围内不要把结构建立在陡坡处,若要建立则需要做一些加固防范措施。
3 结 论
建立隧道洞口段三维有限元模型,探讨了在地震荷载激励下,隧道洞口段在不同软岩弹性模量、泊松比以及坡度下的动力响应规律通过对比分析可得到如下结论:
(1) 对于不同软岩弹性模量从2 GPa到5 GPa隧道洞口段进行数值模拟,随着弹性模量的增加,隧道洞口段的塑性区分布逐渐减小,隧道洞口段各监测点的最大加速度随着弹性模量在适当的范围内的增加而先增加后减小,并且随着隧道洞口段监测点的高程的增加而逐渐递增,拱顶的加速度峰值明显大于拱腰处的加速度峰值,拱腰处的加速度峰值要大于拱脚处的加速度峰值,而拱脚与拱腰之间的加速度峰值差别不大,监测点的水平位移峰值随着软岩弹性模量的增加而逐步递减,且高程越大递减得越快。
(2) 对于不同软岩泊松比从0.32~0.38隧道洞口段进行数值模拟,随着泊松比的增加,隧道洞口段的塑性区分布慢慢减小,隧道洞口段监测点的加速度峰值随着软岩泊松比的增加明显变大,同时随着监测点高程的变大而增加;但是最大水平位移却随着泊松比的增大变化不大,只是缓慢的递减,而随着高程的增加具有明显的变大趋势。
(3) 对于不同坡度从30°~60°隧道洞口段进行数值模拟,随着坡度的增加,隧道洞口段的塑性区分布明显减小,隧道洞口段的监测点的加速度峰值和水平位移峰值都是随着坡度角度的增大而逐渐增大,但是位移加速度峰值相对于加速度峰值增加的缓慢一些,并且高程越大,加速度峰值越大。

