多系统双频精密单点定位不同模型下性能比较分析

陈杰, 刘正才,苏珂,郭佳宾

(1.湘潭大学 土木工程与力学学院,湖南 湘潭411105; 2.中科院上海天文台,上海200030; 3. 南京信息工程大学遥感与测绘工程学院,江苏 南京210044)

0 引 言

全球卫星导航系统(GNSS)主要由美国GPS，俄罗斯GLONASS，中国北斗卫星导航系统(BDS)，欧盟Galileo四大系统组成.IGS建立了多GNSS实验(MGEX),用于跟踪、整理和分析所有可用的GNSS信号,精密单点定位(PPP)是众所周知的定位技术,于1997年被首次提出并用于GPS,因其高精度、熟练性、稳定性和灵活性而被广泛使用[1]. 为了在更短的收敛时间和更高的精度下获得更好的结果,多系统的组合使用相比仅使用GPS的PPP的准确度、可靠性和可用性都有显著提高[2]. 基于原始观测的PPP提供了替代且稳健的解决方案,在处理未来多频率GNSS数据时更灵活,有避免噪声放大并且能够提取电离层延迟的优点. 推导了基于原始观测的PPP模型,并在定位、对流层和电离层建模方面表现出更好的性能和潜力[3].

在PPP模式下GPS/GLONASS组合观测获得初步结果并没有明显改善收敛时间,可能由于可用的GLONASS卫星有限[4]. 在随后几年有关于GLONASS和GPS/GLONASS的研究中,开发了无电离层组合GPS/GLONASS的模型. 结果表明,与仅使用GPS相比,组合的GPS/GLONASS在定位性能和收敛时间有明显改善,但其中并没有考虑GLONASS的伪距频间偏差(IFB)[5]. 由于GLONASS的伪距IFB对PPP有重要影响,伪距IFB与接收机类型和天线类型相关[6],单一化的模型难以表达,考虑到伪距IFB后对GLONASS的定位性能有所提升[7]. 随着BDS的发展,在仅使用BDS的静态和动态模式下,定位结果能够获得厘米级的精度[8]. 由于GPS/BDS PPP组合的实现,与单BDS PPP相比,BDS/GPS可明显提高收敛时间和定位精度[9]. 本文通过采用双频消电离层模型和非差非组合模型实现了单系统、双系统、四系统双频PPP，并从定位精度、收敛时间两个方面对定位性能进行分析并给出相应结论. 对GLONASS特有的伪距IFB进行估计以提升PPP的定位性能.

1 PPP模型

1.1 观测模型

一颗GNSS卫星j,第i(i=1,2)频率上的测码伪距和载波相位观测值可以表示为[10]

(1)

(2)

1.2 无电离层模型(IF-PPP)

电离层延迟误差通过观测值之间组合来进行消除,根据电离层误差和信号频率成反比的特性,可以根据不同频率的观测值进行线性组合来消除电离层的影响,以频率f1和f2为例,双频无电离层模型可以表示为[11]

(3)

(4)

1.3 非组合模型(UC-PPP)

无电离层模型通过对原始观测值组合来消除电离层的影响,但同时会放大观测噪声并丢失电离层延迟有用信息,非差非组合模型是一种统一的GNSS数据处理模型,对任何频率都可以建立观测方程,其观测模型可以表示为[12]

(5)

(6)

1.4 GLONASS伪距IFB模型

与GPS不同的是，GLONASS采用的是频分多址(FDMA),不同的卫星有不同的频率和载波,忽略IFB，导致IFB不能被接收机钟和电离层参数吸收,与频率相关的部分在伪距残差中体现[13],采用两种不同的模型,一种是模型化伪距IFB为频率数的二次多项式,其伪距IFB模型化为

(7)

(8)

2 数据和处理策略

为研究分析不同系统不同策略下对PPP的影响,采用MGEX的10个测站BRAZ、 BRUX、 KZN2、 NICO、 NKLG、 EUSM、 KARR、 MIZU、 ALIC、GAMG的数据,测站的地理分布图如图1所示,所选的站点都支持BDS、GPS、GLONASS和Galileo信号,观测时间为2018年1月1日-1月7日.

图1 所选测站地理分布

所选站点使用原始观测数据,对于GPS和GLONASS选择L1和L2频率,BDS和Galileo分别选择B1和B2以及E1和E5a频率,处理模式有:GPS(G)、GPS/GLONASS(GR)、GPS/BDS(GC)

和GPS/GLONASS/Galileo/BDS(GREC). 将GPS和GLONASS的码和相位观测值分别设为0.3 m和0.003 m,BDS和Galileo的码和相位分别设为0.6 m和0.004 m[14]. 对于GLONASS伪距IFB,不同接收机的类型对伪距IFB有不同的影响,所选测站接收机类型有LEICA GR25、TRIMBLE NETR9、SEPT POLARX5TR和JAVAD TRE_3,对GLONASS和GPS/GLONASS采用不同的估计伪距IFB模型对定位性能进行评估,其中包括忽略伪距IFB、采用伪距IFB为频率二次多项式模型(IFB1)和对每颗GLONASS卫星评估一个伪距IFB参数模型(IFB2). 表1示出了数据处理策略和改正模型的详细信息.

表1 多系统PPP处理策略

3 PPP性能比较分析

通过MGEX的10个测站不同系统之间组合采用单频PPP(IF0)、双频无电离层PPP(IF1)和双频非差非组合PPP(UC)对定位性能进行测试,同时对单系统GLONASS和组合系统GPS/GLONASS的伪距IFB采用频率二次多项式模型(IFB1)和对每颗GLONASS卫星评估一个伪距IFB参数模型(IFB2)进行定位性能分析,定位性能包括收敛时间和定位精度,定位误差小于0.1 m并保持在0.1 m直到计算结束则为收敛.

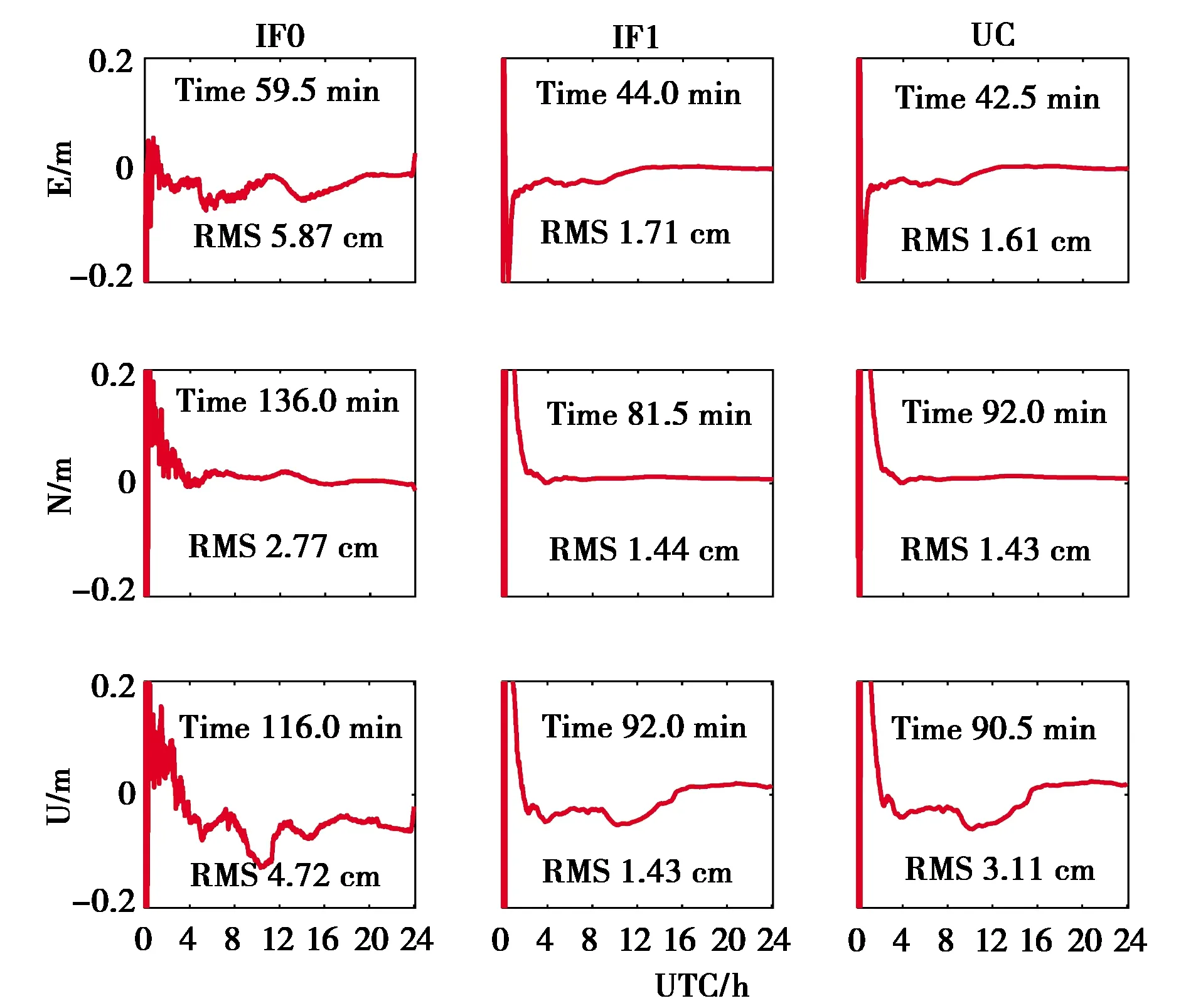
图2 KARR站不同模型下BDS PPP定位误差比较

图3 ALIC站卫星数和PDOP值

图2中示出KARR站2018年1月1日BDS在不同模型下静态PPP E(东)、N(北)和U(天顶方向)的定位误差,IF-PPP模型和UC-PPP模型定位性能基本相同,其定位精度和收敛时间优于单频PPP模型,图3中给出ALIC站2018年第2日BDS、GPS/BDS和GPS/Galileo/GLONASS/BDS的卫星数和位置精度因子值(PDOP),BDS的平均卫星数和PDOP值分别为7.1和4.9,PDOP值上下波动幅度较大,GPS/BDS平均卫星数和PDOP值分别为16.3和1.4,GPS/Galileo/GLONASS/BDS平均卫星数和PDOP值分别为27.1和1.0,PDOP较为平稳,多系统的组合不仅增加卫星数,而且改善了卫星间的几何构型.

图4 十个测站连续四天E、N和U平均收敛时间

图5 10个站连续四天E、N和U平均RMS值

图4示出了10个站连续四天在不同模型下不同组合系统E、N和U方向的平均收敛时间,图5示出E、N和U方向的RMS值,在单系统、双系统和四系统中,两种PPP模型在定位性能上要优于单频PPP.对于BDS PPP其定位性能要劣于GPS PPP,主要是因为卫星的几何分布和定轨精度的影响,导致BDS PPP的定位精度差和收敛时间长,但组合系统GPS/BDS PPP的定位性能要优于BDS PPP,在E、N和U方向对于不同的模型收敛时间缩短20 min左右,定位精度提高1.6 cm左右. 组合系统GPS/GLONASS和GPS/Galileo/GLONASS/BDS相比于单系统GPS定位性能略有提升,同样也证明多系统增加卫星数并改善卫星的几何结构,可提高PPP的定位性能.

图6 MIZU站估计IFB下PPP性能比较

图6示出了MIZU站2018年1月3日采用不同的估计GLONASS伪距IFB模型下进行定位性能比较结果,GPS PPP定位性能要优于GLONASS PPP定位性能,主要是GLONASS的定轨精度和钟差产品的精度相比GPS要差. 图7示出MIZU站2018年1月3日伪距观测残差序列图,不同颜色表示不同的卫星,GPS伪距残差值相比GLONASS的伪距残差值小,其观测值的质量相比GLONASS的观测值质量要好. 两种考虑IFB模型均比不考虑IFB的残差值要小,IFB2模型的残差值要小于IFB1模型,IFB2模型更优于IFB1模型. 表2示出10个测站GLONASS和GPS/GLONASS连续三天PPP平均收敛时间和RMS值,在单系统GLONASS PPP和组合系统GPS/GLONASS PPP中,GPS/GLONASS PPP定位精度和收敛时间要优于GLONASS PPP定位. IFB2相比于忽略IFB在E、N和U方向上收敛时间分别缩短约8 min、2 min和11 min,在定位精度上分别提高约0.1 cm、0.06 cm和0.15 cm;IFB1相比于忽略IFB在E、N和U方向上收敛时间分别缩短约3 min、1.4 min和6 min,在定位精度上分别提高约0.04 cm、0.04 cm和0.09 cm,IFB2模型比IFB1模型在定位性能方面略好.

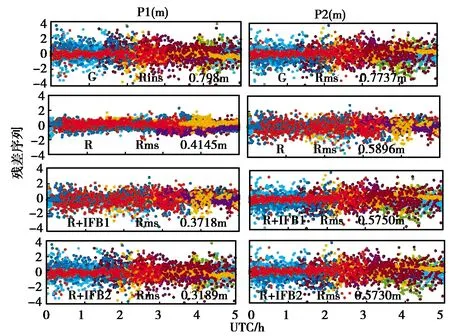
图7 MIZU站伪距观测残差序列图

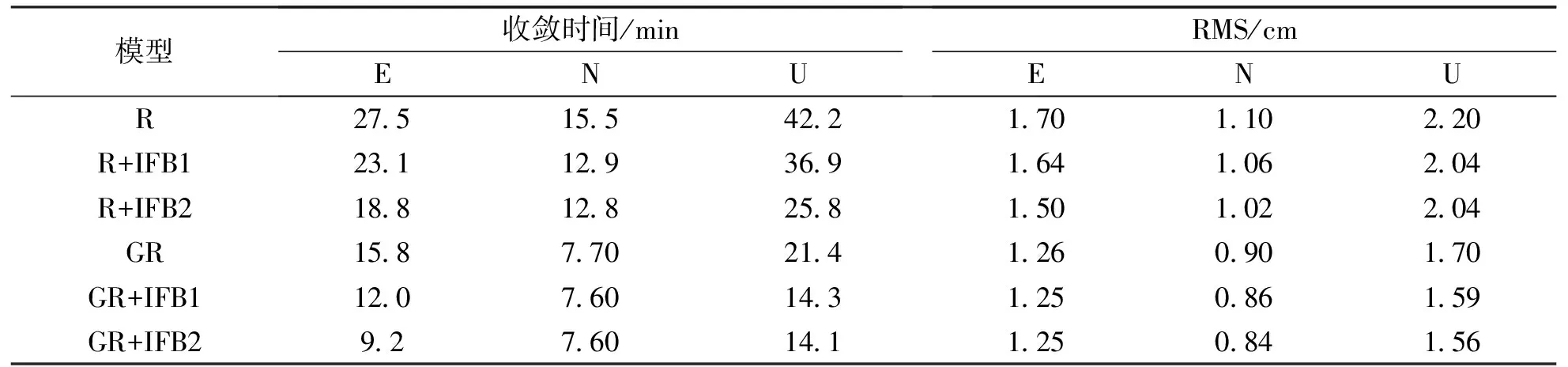
表2 10个测站GLONASS和GPS/GLONASS连续三天PPP平均收敛时间和RMS值

4 结 论

本文通过MGEX 10个测站对GPS、BDS、GLONASS和Galileo多系统PPP模型(IF-PPP, UC-PPP)进行定位性能分析,结果表明两种PPP模型在定位性能上相当. 在单系统、双系统和四系统中,两种PPP模型在收敛性能要优于单频PPP,PPP收敛时间缩短20 min左右,定位精度提高1.6 cm左右,BDS和GLONASS PPP的定位性能要劣于GPS PPP,因其钟差产品、卫星分布和定轨的精度较差. 但组合系统能够提高卫星数目改善几何构型,并且能够提高定位精度和定位抗差性. 另外,对单系统GLONASS和组合系统GPS/GLONASS中GLONASS伪距IFB进行估计,结果表明估计每颗GLONASS卫星伪距IFB模型比GLONASS伪距IFB为频率二次多项式模型在PPP定位性能上较优,考虑GLONASS伪距IFB相比忽略伪距IFB能够提升PPP定位性能,使PPP收敛时间缩短,定位精度提高.