一种移动FH-FSK通信多普勒估计方法
王维伟, 孙慧嵩, 颜宏璐
一种移动FH-FSK通信多普勒估计方法
王维伟1, 孙慧嵩2,3,4, 颜宏璐2,3,4
(1. 大连测控技术研究所, 辽宁 大连, 116013; 2. 哈尔滨工程大学 水声技术重点实验室, 黑龙江 哈尔滨, 150001; 3. 工业和信息化部 海洋信息获取与安全工信部重点实验室(哈尔滨工程大学), 黑龙江 哈尔滨, 150001; 4. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨, 150001)
在进行水下移动通信时, 多普勒效应会对信号造成影响, 常规估计多普勒频偏因子的方法是通过发射多普勒敏感脉冲信号进行估计。在跳频通信-频移键控(FH-FSK)通信中, 单个码片具有较好的多普勒敏感性, 文中采用32个跳频码片作为同步信号, 对同步信号中逐个码片进行多普勒因子估计。在多普勒因子选择时, 提出进行2次卡尔曼滤波后再取中值的方法, 使估计值更接近准确值。考虑到多普勒效应对同步造成的影响, 采用同步后进行多普勒补偿再次同步的方法, 进一步减少解码时由于同步偏差较大带来误判的可能性。仿真试验结果表明, 基于卡尔曼滤波的多普勒因子选择方法能使多普勒估计值更贴近理论值, 且重同步后通信误码率降低。该方法能够提高多普勒估计精度, 进一步提升移动FH-FSK通信性能。
水下通信; 跳频通信-频移键控通信; 多普勒估计; 卡尔曼滤波
0 引言
近些年来, 随着水下航行器的快速发展, 移动水声通信越来越受到人们的重视[1]。水下环境的复杂性以及运动产生的多普勒效应都会对相互通信造成影响, 使通信的可靠性变差[2]。跳频通信(frequency hopping, FH)通过扩展频谱的方式提高了系统的抗干扰能力, 使系统能够在复杂信道条件下实现远距离的可靠通信。在实际应用中, FH常与频移键控(frequency-shift keying, FSK)调制方式相结合形成FH-FSK通信[3]。
美国海军Seaweb水声通信网络使用了传输速率为80 bit/s的FH-FSK通信技术进行试验研究, 发现在浅海信道中该方案比差分相移键控(diffe- rential phase shift keying, DPSK)方案更稳健[4]。中科院声学所为“蛟龙号”深海载人航行器所研制的水声通信系统中集成了FH-FSK通信体制, 试验结果显示, 在航行器启动螺旋桨推进器的情况下, 在所集成的4种通信方式中, 只有FH-FSK系统可以正常工作[5]。FH-FSK通信系统凭借良好的可靠性和保密性, 以及能进行多址通信的优势, 在水声通信网络和水声遥控等领域得到广泛应用。水声通信系统的研究主要在于如何降低信道对通信信号的畸变影响[6], 所以水声FH-FSK通信系统的高可靠性同步检测和多普勒估计与补偿问题值得进一步研究[7]。文献[8]通过在通信频带内划分独立的频带, 用导频的方式来估计多普勒频偏, 并对该方法进行了仿真, 仿真结果表明, 基于导频的多普勒频移估计及补偿方法具有较强的抗窄带干扰能力。
文中主要研究移动FH-FSK通信中多普勒估计技术, 由于单个跳频码片具有较好的多普勒敏感性, 因此, 可以对已知频率的跳频码片进行多普勒估计, 进而得到多普勒频偏因子。该项技术的特点在于基于Goertzel能量检测方法进行同步, 并采用卡尔曼滤波方法进行多普勒估计改进。
1 多普勒效应对信号的影响
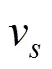
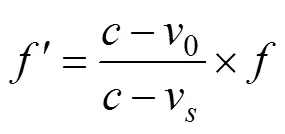
当声源静止时, 信号的频偏和时长变化对应的表达式分别为
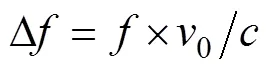

2 多普勒效应影响下的同步设计
良好的同步是正常通信的前提, 常规的同步方法可分为外同步法和内同步法2种。外同步法是利用相关性较好的信号作为同步头, 利用同步信号的相关性建立同步, 这种方法简单且同步速度快, 但同步头会占用信道频率资源和信号功率, 且信号隐蔽性较差。内同步法是基于发送信号本身进行同步, 这种方法不需要其他辅助信号, 而是直接在通信信号中提取同步信息, 这样不仅增加了通信的频带利用率, 而且提高了通信的隐蔽性[10]。文中同步信号由32个跳频码片构成, 考虑到在移动通信中多普勒效应会对同步信号造成影响, 由于信号波形发生了变化, 采用拷贝相关法不能达到较好的效果。因此, 文中采用基于Go- ertzel能量叠加检测算法的内同步法实现同步。
2.1 帧结构设计


图1 信号的帧结构
2.2 模型仿真设计


2.3 Goertzel算法
传统的基于快速傅里叶变换(fast Fourier transform, FFT)获得频谱能量的方法计算的是窗内所有频点的能量, 不符合同步时能量检测的要求。Goertzel算法[11]是一种比FFT计算效率更高, 能在给定信号中求出某一特定频率能量的方法。在通信中, 由于信息频率是不断跳变的, 若信号窗长度和单个跳频信号长度相同时, 在同一个窗函数内可能出现2个频点。因此, 只对单一频点能量进行计算的Goertzel算法更符合检测要求。
2.4 Goertzel能量检测法
FH-FSK通信中同步的方法是基于Goertzel能量叠加检测进行的。FH-FSK通信中的各个频点都按照一定规律进行跳变, 每个频点对应的信号都具备一定能量, 因此可以按照通信中同步信号对应频率的能量进行叠加, 通过能量峰值位置判断信号的起始位置。图2给出了通过Goertzel能量检测方法确定同步信号位置的过程。由于同步信号频率是已知的, 首先将频率按照大小进行排序, 然后长度为、重叠长度为的窗函数依照频率的顺序依次计算窗内当前频点对应的能量, 之后按照同步码片中各码片频点的顺序将能量值进行移位叠加, 移动窗长为形成能量峰值, 最后, 根据能量峰值的位置确定同步码片的位置。

图2 Goertzel能量检测同步过程
3 基于码片的多普勒估计技术
3.1 多普勒估计方法


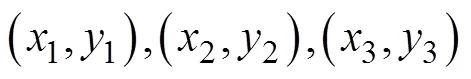

图3 离散傅里叶变换能量拟合示意图


得到表达式为

3.2 多普勒估计算法的改进

在进行多普勒因子选择时, 常规的处理方法是从均值或中值中选取。由于水声信道环境复杂, 在进行多普勒因子估计时存在估计不准的情况, 如果存在多个码片偏差较大, 采用均值法会使通信估计偏差增大, 甚至导致估计错误。均值法只能在估计值中的所有值都是准确估计时, 才能够确保更高的精度。如果估计值中有一半以上估计准确, 中值法就不会产生较大的偏差, 但是精度不能保证。从图4中可以看出, 由于每个码片多普勒因子偏差较大, 不适合采用均值法, 但是采用中值法又不能确保多普勒因子的估计精度。由图5中给出的信噪比在-10~10 dB时, 分别采用均值法和中值法进行多普勒因子选取情况, 可以看出, 采用中值法进行取值更接近真实值, 因此采用中值法选取性能略优于均值法。鉴于这2种方法都存在一定的误差, 因此在中值法选取的基础上, 提出一种新的方法——基于卡尔曼滤波的多普勒因子选择。

图4 码片对应多普勒因子估计情况

图5 中值法和均值法估计结果
3.3 卡尔曼滤波处理
卡尔曼滤波是一种高效的线性估计算法。将前一时刻的状态估计值和当前测量的信息进行融合得到当前时刻的状态估计值, 通过递推方式将新产生的估计值与测量值不断融合进行修正, 从而得到一个最优状态估计[13]。若测量系统是线性的, 该系统可以表达为

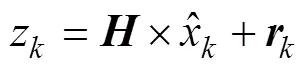
4 算法仿真及分析
首先对多个已知频率码片分别进行多普勒估计, 然后对计算得到的多个多普勒因子进行卡尔曼滤波处理, 再对滤波后的结果进行取值, 从而得到新的多普勒因子估计值。这种方法能够提高估计精度, 进一步提升系统估计的准确性。考虑仿真中要有足够的数据量进行统计分析, 仿真次数设置为500次, 单次数据量达到256 bit, 可以实现最小误码率10–5的仿真结果。
图7中给出了信噪比为–5~10 dB时, 采用3种方法对应的估计偏差, 从图中可以看出, 三者与理论值相差量级限制在10–4, 在当前速度下经过2次卡尔曼滤波后再进行取值, 通信的估计精度得到了一定的提升, 相比于直接取中值, 通信性能提升了10–5左右。
文中研究固定速度下多普勒效应对码片的影响, 即假设多普勒效应对信号每个码片频率的影响相同。前文介绍了根据32个已知频率估计出多普勒因子的方法, 在估计出多普勒因子后需要对信号进行多普勒补偿, 即计算出经多普勒效应影响后信号码长及对应频率, 从而消除多普勒效应对信号的影响, 确保通信的有效性。
图8中给出了在精准同步下多普勒补偿后的通信性能。图中“ + ”标识表示不进行多普勒补偿的情况, 通信的误码率维持在0.5左右, 无法进行通信; “ * ”标识表示按照通信预设速度进行补偿时的通信性能曲线, 可以看出如果准确估计多普勒因子, 可以消除多普勒效应对通信的影响。“”标识为采用2次卡尔曼滤波后取中值, 估计出多普勒因子进行补偿后通信的误码率曲线, 虽然没有完全消除多普勒效应的影响, 但是很大程度上改善了通信的性能, 当信噪比高于–6 dB时, 经过信道编码后能够纠正传输错误, 实现无误码传输。“△”标识和“★”标识分别对应一次卡尔曼滤波取中值和直接取中值时通信的误码率曲线; 说明采用2次卡尔曼滤波的方法比这2种方法性能更为优异, 在误码率为10–3时, 分别获得2 dB和3 dB增益。

图6 多普勒因子选择方法比较

图7 多种方法性能比较
Fig.7Performance comparison of different methods

图8 精准同步下多普勒估计性能
Fig.8 Doppler estimation performance under precise synchronization
按照发送端和接收端双方已有的参数对同步信号进行设置, 采样率为48 kHz, 通信频带带宽为4 kHz; 采用在同步位置随机取值的方法, 进行200次真实值选取, 从而忽略同步位置偶然性影响。在同步偏差设为1/2码片长时, 图9中给出了速度为4 m/s时通信对应的同步错误概率。图中“”标识表示拷贝相关方法进行同步时的情况, 信噪比为-15 dB时, 同步错误概率大于95%, 无法通信。而同样信噪比条件下, “ * ”标识则表示基于Goertzel能量检测方法的同步错误概率小于10%, 通信准确性更高。可以看出, 基于Goertzel能量检测方法在移动平台下进行通信具有较好的适应性, 相对于拷贝相关方法能够相对准确地进行同步; Goertzel能量检测方法由于采用的对应频率能量叠加的方式, 所以使得信号在存在多普勒效应的情况下, 不会出现较大的偏差。而拷贝相关方法本质上是基于信号本身的相关, 由于信号波形发生了变化, 所以不能达到较好的效果。
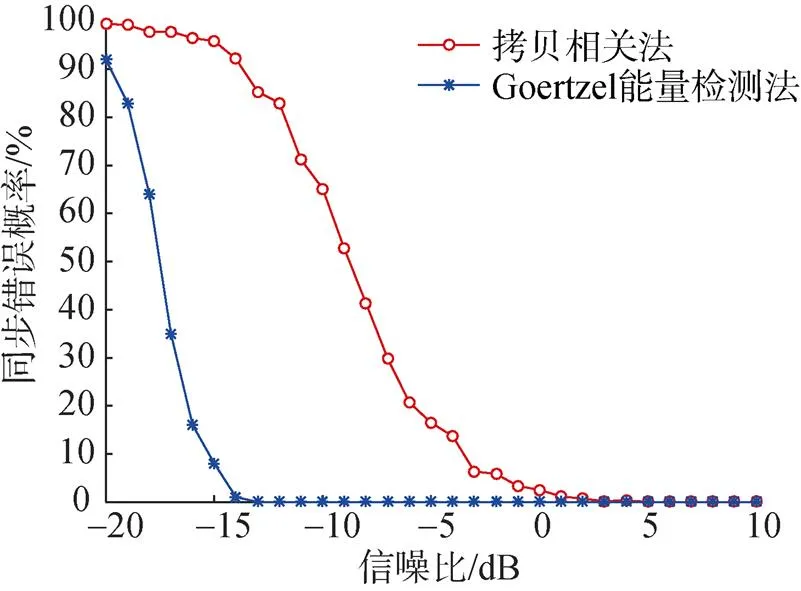
图9 速度为4m/s时同步性能
图10中给出了同步补偿后FH-FSK水声通信的性能。图中“ * ”标识表示基于Goertzel能量检测方法进行同步且准确估计多普勒因子的情况下通信的性能; “”标识表示采用重同步的通信性能; “△”标识表示采用一次Goertzel能量检测方法即无重同步时通信性能。信噪比为-5 dB时, 有重同步情况下的误码率小于无重同步时的误码率, 并且两者都小于10-2, 可以进行通信。可以看出, 单独采用Goertzel能量检测方法进行同步虽然能够大致确定信号的位置, 但是由于某些点估计偏差较大在解码时依旧发生错误。因此, 通过同步后进行多普勒补偿, 然后再次同步的方法能够进一步减少解码时由于同步偏差较大带来误判的可能性。

图10 同步补偿后系统性能
5 结束语
文中基于Goertzel能量检测方法进行同步, 并估计出同步码片对应的多普勒因子, 采用卡尔曼滤波的方法对估计结果进行滤波处理, 进一步提升移动FH-FSK通信性能。考虑到多普勒效应对同步造成的影响, 采用同步后进行多普勒补偿再重新同步的方法, 进一步减少解码时由于同步偏差较大带来误判的可能性。文中主要研究固定速度下多普勒效应对信号造成的影响, 然而实际应用中, 移动平台运动复杂, 需要进一步研究变速情况下对多普勒因子的估计。虽然估计出了多普勒因子, 但是并未完成消除多普勒效应对通信造成的影响。由于DFT插值法不能确保每个码片的估计准确性, 可以采用准确性更高的多普勒估计方法, 进一步提升通信性能。
[1] Yin J W, Ying H J, Guo L X. Study on Point-to-point Mobile Underwater Acoustic Communication[J]. Acta Physica Sinica, 2008, 57(3): 1753-1758.
[2] 惠俊英, 生雪莉. 水下声信道[M]. 北京: 国防工业出版社, 2007.许肖梅. 水声通信与水声网络的发展与应用[J]. 声学技术, 2009, 28(6): 811-816.
Xu Xiao-mei. Development and Applications of Underwater Acoustic Coumunication and Networks[J]. Technical Acoustic, 2009, 28(6): 811-816.
[3] Porter M B, Mcdonald V K, Baxley P A. SignalEx: Linking Environmental Acoustics with the Signaling Schemes[C]//Oceans 2000 MTS/IEEE Conference and Exhibition. Providence, USA: IEEE, 2000: 595-600.
[4] 朱维庆, 朱敏, 武岩波, 等. 载入潜水器“蛟龙”号的水声通信信号处理[J].声学学报, 2012, 37(6): 565-573.
Zhu Wei-qing, Zhu Min, Wu Yan-bo, et al. Signal processing in Underwater Acoustic Communication System for Manned Deep Submersible “Jiaolong”[J]. Acta Acustica, 2012, 37(6): 565-573.
[5] 董继刚. AUV水声通信系统研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
[6] 范巍巍. AUV水声跳频通信关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
[7] 申晓红, 王海燕, 赵宝珍, 等. 基于混沌序列的水声跳频通信系统研究[J]. 西北工业大学学报, 2006, 24(2): 180-184.
Shen Xiao-hong, Wang Hai-yan, Zhao Bao-zhen, et al. A More Secure Underwater Acoustic Frequency-Hopping Communication System Based on Chaotic Sequence[J]. Journal of Northwestern Polytechnical University, 2006, 24(2): 180-184.
[8] Caley M, Duncan A. Investigation of Underwater Acoustic Multi-path Doppler and Delay Spreading in a Shallow Marine Environment[J]. Acoustic Australia, 2013, 41(1): 20-28.
[9] 胡莉, 张力伟, 周希元. 帧同步检测技术的研究进展[J]. 无线电工程, 2009, 39(2): 12-15.
Hu Li, Zhang Li-wei, Zhou Xi-yuan. Research Advances in Frame Synchronization Detection[J]. Radio Engineering of China, 2009, 39(2): 12-15.
[10] Mitra S K. Digital Signal Processing a Computer- Based Approach[M]. 4th Edition. New York: McGraw-Hill Higher Education, 2010.
[11] 魏清洁, 王玉彬. 二元一次函数曲线拟合的Matlab实现[J]. 德州学院学报, 2011(s1): 148-151.
[12] Kalman R E. A New Approach to Linear Filtering and Prediction Problems[J]. Journal of Basic Engineering Transactions, 1960, 82(1): 35-45.
A Doppler Estimation Method of Mobile FH-FSK Communication
WANG Wei-wei1, SUN Hui-song2,3,4, YAN Hong-lu2,3,4
(1. Dalian Scientific Test and Control Technology Institute, Dalian 116013, China; 2. Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China; 3. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China; 4. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China)
During underwater mobile communication, the signals will be affected by Doppler effect. The conventional method for estimating the Doppler frequency offset factor adopts transmission of Doppler sensitive pulse signal. In frequency hopping frequency-shift keying(FH-FSK) communication, single chip has better Doppler sensitivity. In this paper, 32 frequency hopping chips are used as synchronizing signals, and Doppler factor estimation is performed for the chips one by one in the synchronizing signal. In the Doppler factor selection, two times of Kalman filtering are performed to obtain the median value so as to make the estimated value more accurate. Considering the influence of the Doppler effect on synchronization, the method of Doppler compensation after synchronization and resynchronization is adopted to further reduce the possibility of misjudgment caused by large synchronization deviation during decoding. Simulation results show that the Doppler factor selection method based on Kalman filter can make the Doppler estimation closer to the theoretical value and reduce the bit error rate after resynchronization. It is proved that this method can improve the accuracy of Doppler estimation and the performance of mobile FH-FSK communication.
underwater communication; frequency hopping frequency-shift keying(FH-FSK) communication; Doppler estimation; Kalman filtering
TJ630.34; TN929.3
A
2096-3920(2019)06-0629-07
10.11993/j.issn.2096-3920.2019.06.005
2019-04-06;
2019-05-21.
国家重点研发计划(2018YFC0308500, 2017YFC0305702); 中国科学院水声环境特性重点实验室开放课题(SHHJ- KFKT-1801).
王维伟(1982-), 男, 高级工程师, 主要研究方向为水声通信技术.
王维伟, 孙慧嵩, 颜宏璐. 一种移动FH-FSK通信多普勒估计方法[J]. 水下无人系统学报, 2019, 27(6): 629-635.
(责任编辑: 许 妍)

