基于PMF算法的水下地形辅助导航性能研究
徐振烊, 张静远, 王 鹏, 王新鹏
基于PMF算法的水下地形辅助导航性能研究
徐振烊, 张静远, 王 鹏, 王新鹏
(海军工程大学 兵器工程学院, 湖北 武汉, 430033)
针对目前水下地形辅助导航性能受诸多因素影响而无法得到最佳发挥的问题, 采用双线性插值法制备了相应分辨率的水下数字地图, 基于直接概率准则的质点滤波(PMF)算法, 较为全面地仿真分析了水下航行器航速、测深误差、航向误差、速度误差、初始位置偏差, 以及水下地形特征等因素对导航性能的影响规律, 对PMF算法在复杂条件下的应用性能进行了剖析。仿真结果表明, PMF匹配算法在复杂条件下具有较强的稳定性; 一定范围内, 该算法对速度和航向表现出较好的抗误差能力, 但速度太低会严重影响匹配性能; 该算法受测深误差和初始位置偏差的影响程度较大, 对测深精度和惯性导航系统提出了相对较高的要求; 该算法地形适应性较强, 但丰富地形更有利于匹配导航; 通过合理地选择应用参数, 可有效降低匹配误差, 提高导航性能。该项研究可为日后匹配算法在水下导航工程实践中的应用提供参考。
水下航行器; 地形辅助导航; 数字地图; 质点滤波算法; 导航性能
0 引言
目前, 随着水下遂行任务的多样化, 潜艇、无人水下航行器、鱼雷、自航水雷等水下航行器对导航精度的要求越来越高。水下地形辅助惯性导航可有效降低水下航行器的导航定位误差, 增强隐蔽性, 提高生存能力, 为水下高精度自主导航定位提供重要保证, 受到各国的高度重视[1-3]。
水下环境相对复杂, 匹配导航精度受多种因素影响和制约, 其中, 匹配算法是水下地形匹配辅助导航核心技术。目前地形匹配算法主要有基于地形轮廓匹配(terrain contour matching, TERCOM) 算法、基于扩展卡尔曼滤波的惯性地形辅助导航(sandia intertial terrain-aided navigation, SITAN)算法和基于直接概率准则的贝叶斯估计法等。前2种算法前期已在陆上得到了较为广泛的应用, 表现出了良好的匹配特性[4-6]。但TERCOM 算法属于相关批处理, 有一定的延时性, 无法进行实时匹配, 而SITAN算法需要对地形作近似线性化处理, 在这一过程中势必会产生误差。鉴于研究的问题是关于非线性的状态估计问题, 因而选择基于直接概率准则的质点滤波(point-mass filter, PMF)算法。Bergman[7]针对陆上飞行器地形辅助导航问题, 仿真证明了 PMF 算法的可行性。随后, Karlsson[8]、Yingrong[9]及Anonsen等[10]相继将该方法运用到水下, 提出了基于水下环境的PMF地形匹配算法。Meduna等[11]利用性能不同的自主水下航行器进行了相关海试, 验证了滤波算法能够克服测量设备精度对匹配结果的影响。谌剑等[12]分析了网格分辨率与匹配算法定位精度的关系, 讨论了通过合理选取网格分辨率提高PMF算法水下匹配定位精度的可行性。刘洪等[13]对PMF算法进行了相应改进, 并验证其在水下地形匹配导航中的地形适应性及可行性。
目前对地形辅助导航的研究较多地集中于匹配算法改进上, 对其他影响因素与匹配误差间的关系研究相对较少或者仅仅针对某一两个因素进行分析, 目的多在于验证算法的可行性, 而针对滤波算法开展的多因素与匹配性能的关系研究较少且不全面, 理不清其间关系就会制约匹配算法在地形辅助导航中更好的应用。文中首先根据某海域的公开地形水深数据, 通过线性插值法构建相应分辨率的水下数字地图模型; 而后基于PMF匹配算法, 以导航性能为研究对象, 全面分析多因素对匹配性能的影响, 对匹配算法的应用性能进行了更进一步的剖析, 为日后匹配算法在水下地形辅助导航工程中的更好应用、应用参数的选取及匹配区选择提供参考。
1 水下数字地图模型构建
水下环境较陆上相对复杂, 量测工作有一定困难, 工作量大且不易于大范围开展, 高清图像的实时获取也相当困难, 因此通常选择数字高程模型(digital elevation model, DEM)来表达水下地形信息。DEM对地形的表征模型主要分为规则格网结构模型、不规则三角形网模型(triangulated irregular network, TIN)和等高线模型3种。鉴于规则格网结构模型具有便于数据的存储、使用、管理、分析和计算等优点, 文中采用如图1所示的正方形规则格网结构模型(和方向上的格网间距相等), 将对象海域按一定的格网尺寸予以划分以形成二维格网结构。

图1 规则格网结构数字高程模型
水下地形分布不均匀、非线性强, 利用二维随机过程模拟生成的地形不能真实地反映地形实际特征及分布情况。因此, 选取台湾海峡附近东经117.508 3º~117.708 1º, 北纬21.238 0º~23.104 6º海域真实水深数据建立水下数字地图, 如图2所示。
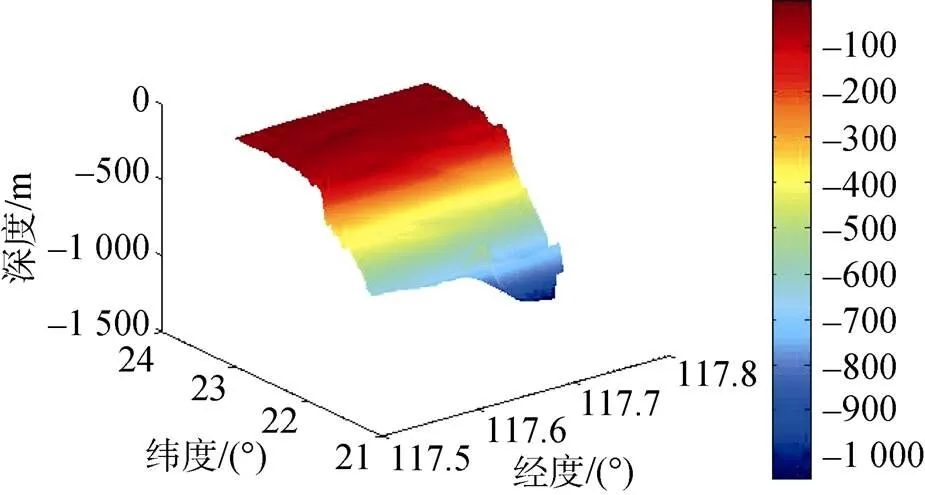
图2 水下地形DEM三维图
鉴于目前技术条件、工作量和水文环境等方面的制约, 制备的水下数字地图分辨率较低, 无法满足水下辅助导航需求。为了研究相关因素对导航定位精度的影响, 需要采用插值法对原始数据进行预处理, 通常采用的插值法有双立方插值法、最近邻插值法和双线性插值法等。双线性插值法计算量较小, 精度基本能够满足要求, 文中采用双线性模型进行插值计算。


式中,0,1,2,3为待定系数, 由下式求得

确定待定系数后便可确定插值点的高程值。
2 PMF匹配算法
水下地形辅助导航主要是利用海底丰富的地形信息, 及测量设备将实时测得的地形水深数据与数字地图基准数据库中的高程数据进行相关处理, 推算出当前航行器的位置, 以修正单纯依靠惯性导航系统产生的误差[14-15]。PMF算法将递推贝叶斯积分简化为在被简化离散了的搜索区域上的有限网格黎曼和。将后验概率密度用网格点集来进行逼近表示, 各个网格点的权值表示状态变量在每个网格点的概率, 解决了非线性模型的线性化近似所带来的一系列问题。
建立二维非线性模型



式中,= 1,…,,= 1,…,, 将权值归一化

测量更新

进一步归一化

根据权值求得逼近后验概率密度, 算出定位估计误差, 如此迭代重复计算, 直至循环到既定次数结束。
3 数值仿真与分析
水下地形辅助导航性能受到航速、测深误差、航向误差、速度误差、初始位置偏差及水下地形特征等因素的影响。为探究各因素对导航性能的影响规律, 以便能更好地合理选择应用参数及匹配区域, 提升导航性能, 文中选用分辨率为40 m的水下数字地图, 采用PMF匹配算法, 对相关条件对匹配性能的影响进行仿真分析。

为了兼顾航行器的任务需求、续航能力及研究的可行性, 同时保证计算速度和搜索效率, 设定搜索区域为正方形, 分辨率为地图分辨率的2倍, 算法每秒匹配1次, 测量噪声为协方差为4的白噪声, 过程噪声为协方差在和方向均为60的白噪声, 针对各研究内容仿真条件予以特别说明, 其他基本仿真条件如表1所示。

表1 仿真参数设定
3.1 航行器速度对匹配结果的影响
航路起始点为(2200 m, 4800 m), 航行器沿方向水平航行, 航向为0°, 每秒匹配1次, 航迹及航路对应水下地形如图3和图4所示。为了探究速度对匹配性能的影响, 航行器航速分别设定为0.5, 1, 2, 4, 8, 10, 12, 15 m/s, 其余参数设定同表1, 图5给出了航速为4 m/s和15 m/s时的大起伏区匹配结果, 航速与匹配误差对应关系如表2所示。
由图5及表2分析可知, 航速对匹配误差有一定影响, 匹配误差随航速的适当增大而呈现减小至基本稳定的趋势, 且收敛速度更快, 匹配效率更高。航速过小, 经过的地形相似性较大, 匹配易受到测深序列中冗余数据的影响, 误匹配率增大, 导致系统匹配误差较大, 匹配效果不理想。随着航速的逐渐增大, 尽可能地使各次测深点位于不同的地图格网中, 加大各匹配点测深差异, 避免了匹配过程中相似地形的干扰, 使获取的地形信息更加丰富有效, 匹配误差得到有效抑制, 渐趋平稳。因此, 实际应用中应根据任务需要, 结合地图分辨率及地形信息丰富程度合理地设定航行器速度。

图3 大起伏区匹配航路图

图4 大起伏区航路实时对应的水下地形

图5 不同航速下的匹配结果

表2 航速与匹配误差对应关系
3.2 测深误差对匹配性能的影响
为了探究测深误差对匹配性能的影响, 航行器测深误差标准差分别设为1, 2, 6, 10, 20, 40 m, 其他仿真条件设定同表1, 仿真结果如图6及表3所示。

图6 不同测深误差下的匹配结果

表3 测深误差与匹配误差对应关系
由图6及表3分析可知, 一定条件下, RMSE和误差均值均随测深误差的增大而增大。测深误差为10 m时, 匹配结果开始发散, 可见匹配性能受深度测量误差的影响较大。这主要是因为PMF算法为实时测量匹配, 每次匹配过程中测深误差都会影响测深序列与数字基准地图的精确匹配, 因此应尽可能地提高测深精度, 降低误匹配率。
3.3 航向误差对匹配性能的影响
为了探究航向误差对匹配性能的影响, 航行器航向误差标准差分别设为0.1, 1, 2, 4°, 其他仿真条件同表1, 仿真结果如图7及表4所示。
由图7及表4分析可知, 随着航向误差的增加, 匹配误差随之增大, 匹配性能变差。当航向误差为2°时, 算法开始发散, 这主要是因为航向误差关乎航行器指示航迹偏离真实航迹的程度, 航行器惯导指示航迹与真实航迹间的物理间距随着航行时间的积累而逐渐增大, 当航向误差超出算法容差范围时, 以致航行到某一时刻时搜索区域无法覆盖真实位置, 严重影响系统匹配性能。

3.4 速度误差对匹配性能的影响
为了探究速度误差对匹配性能的影响, 将航行器的速度误差标准差分别设为0.1, 0.2, 0.5, 1, 2, 4 m/s, 其他仿真条件设定同表1, 仿真结果如图8及表5所示。
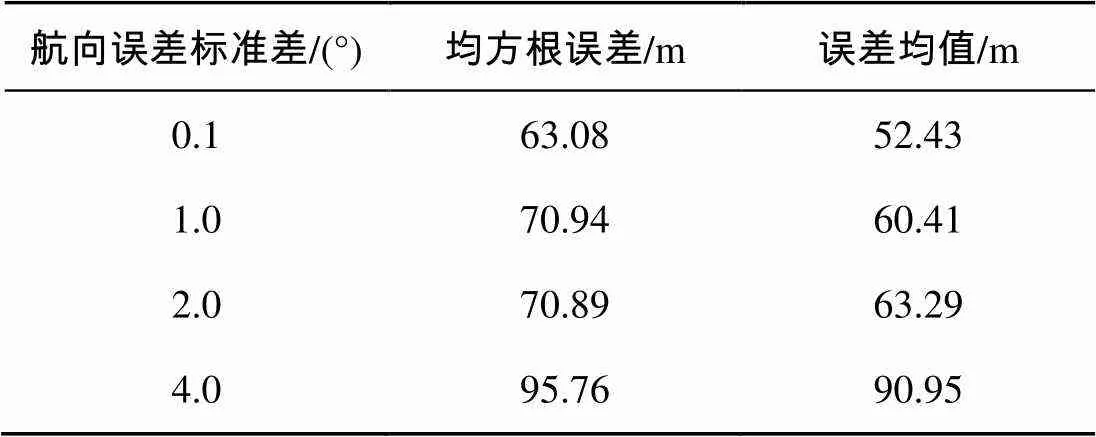
表4 航向误差与匹配误差对应关系

表5 速度误差与匹配误差对应关系
由图8及表5分析可知, 随着速度误差的增加, 匹配误差随之增大, 匹配性能变差, 后期匹配结果有发散的趋势, 匹配不稳定。这主要是因为速度误差影响了航行器指示航迹与真实航迹的间距, 航行器惯性导航指示航迹与真实航迹间的物理间距随着航行时间的积累而逐渐增大。匹配前期由于航行时间不长, 算法逐渐收敛, 当航行时间逐渐增大, 累积误差超出算法容差范围时, 以致航行到某一时刻时搜索区域无法覆盖真实位置, 进而影响系统整体匹配性能, 出现后期匹配不稳定的趋势。
3.5 初始位置偏差对匹配性能的影响
为了探究初始位置偏差对匹配性能的影响, 航行器初始位置偏差分别设为(50 m, 80 m)、(100 m, 80 m)、(200 m, 180 m)、(300 m, 200 m), 其他仿真条件同表1, 仿真结果如图9及表6所示。
由图9及表6分析可知, PMF算法导航性能受初始位置误差影响较大, 在匹配前期匹配误差较大, 收敛速度随初始位置误差的增大而变慢, 主要原因是当惯性导航初始定位精度较差时, 在搜索范围有限的情况下, 匹配误差就会增大, 而增大搜索范围, 同时会加大计算量, 增加计算时间, 影响匹配效率。但PMF算法在一定范围的初始误差下, 定位精度依然较高, 最终使匹配结果渐趋平稳。

图8 不同速度误差下的匹配结果

表6 初始位置偏差与匹配误差对应关系

3.6 地形特征对匹配性能的影响
小起伏或平坦区地形起伏相对较小, 斜坡大起伏区地形变化较大, 水深序列相差较大, 地形丰富程度高于小起伏或平坦区。为了探究地形特征对匹配性能的影响, 分别选择上述地形信息丰富程度不同的2种地形进行仿真分析, 其他仿真条件设定同表1, 2种地形匹配航路图及航路各点对应水下地形如图10和图11所示, 匹配结果如图12所示, 小起伏或平坦区误差均值和均方根误差分别为74.14 m和82.20 m, 大起伏区误差均值和均方根误差分别为59.16 m和72.99 m。
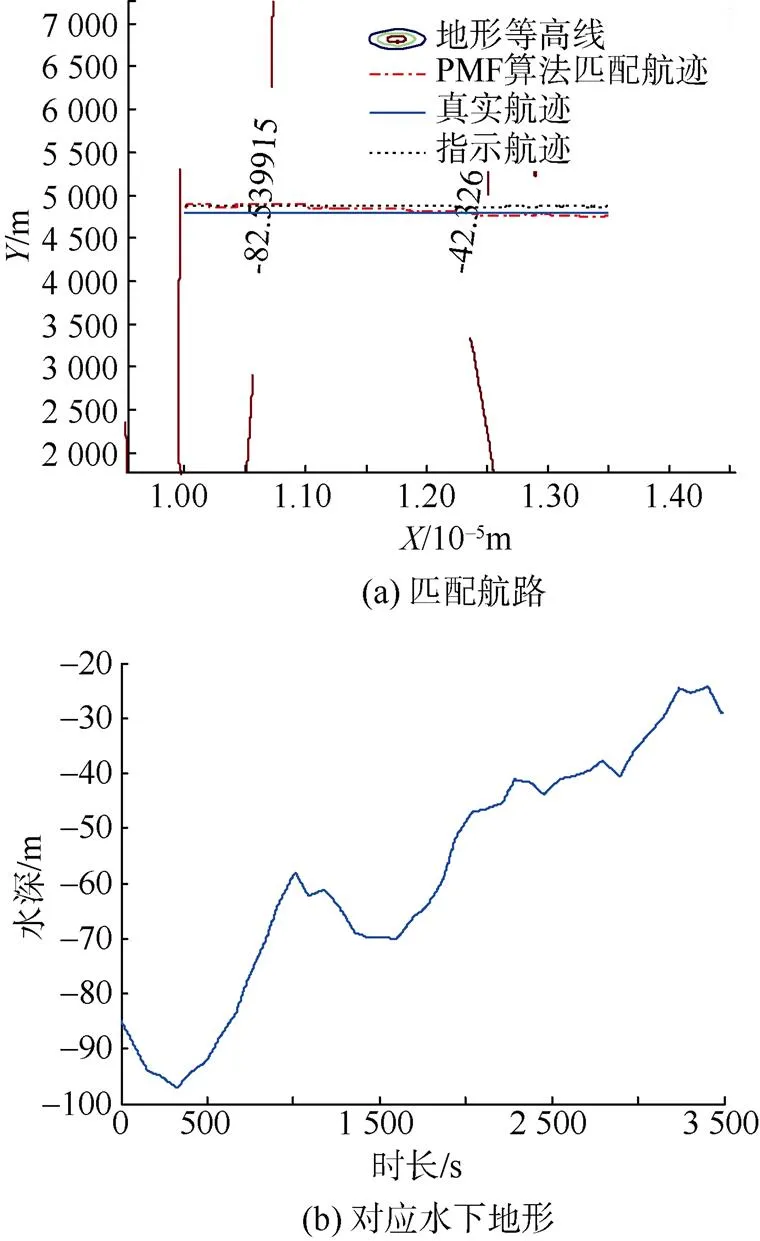
图10 小起伏或平坦区匹配航路及对应水下地形


图12 不同地形匹配结果
由图10~图12可以看出, 在上述的2种地形中, 大概2 500 s以后, 航行器航行到了地形较为平坦区, 水深序列差异变小, 匹配误差随之相应增大, 导航效果较前期变差。说明匹配算法性能的发挥与所选匹配区域的地形特征有很大关联, 地形特征变化明显的区域匹配误差较小, 更有助于匹配导航。
综合对比2种地形, 小起伏或平坦区地形信息不丰富或相对匮乏, 地形起伏变化较小, 匹配误差较大, 导航性能较差; 大起伏区地形信息丰富, 地形起伏变化明显, 匹配误差较小, 收敛速度更快, 导航效果较好, 进一步说明地形信息丰富区比匮乏区更适合导航, 导航效果更好。
4 结束语
文中以PMF匹配算法为支撑, 匹配导航性能为研究对象, 通过仿真分析, 全面细致地讨论了航行器航速、测深精度、航向误差、速度误差、初始位置偏差以及水下地形特征等多因素对导航性能的影响, 对PMF算法的应用性能进行了剖析, 得出了如下相关结论:
PMF算法在地形辅助导航方面具有较强的稳定性和适应性; PMF算法具有实时匹配, 定位精度较高, 抗干扰能力强等优点, 但也存在计算量较大, 收敛速度较慢等问题; 算法在一定的误差范围内可以保证较好的匹配性能, 但随着误差的增大而超出算法承受能力时, 导航性能就会变差; 同等误差条件下, 地形信息丰富的区域较平坦区更利于算法导航性能的发挥; 针对速度、速度误差、测深误差等时间-空间尺度因素对导航性能的影响, 其本质是反映在测量数据与基准数据的偏离度上导致误匹配, 可从提高测量设备精度及控制航行速度上解决此类问题; 针对航向误差、初始位置偏差及地形特征等因素对导航性能的影响, 更多的是对系统整体性能提出了要求, 在适当提高惯性导航系统性能的基础上, 可通过合理设置匹配区数量及质量, 使得航行器导航误差得到及时修正。
在日后工程实践中, 可以根据研究结果合理地进行应用参数设定和匹配地形选择, 减小误差对匹配结果的影响, 综合提高辅助导航性能; 另一方面, 为了满足任务需求, 同时又考虑到经济性, 可根据研究结果进行综合考量, 对相关因素进行取舍和资源分配。
文中是针对辅助导航性能提高而开展的相关误差研究, 相比以往研究较为全面、系统, 通过对系统的进一步了解, 可为日后导航性能在实践应用中的更好发挥, 以及从事相关研究人员提供参考; 采用的匹配算法较以往的TERCOM算法精度更高, 实时性更强。但也存在一定的缺点: PMF算法易受初始误差的影响, 对惯性导航系统的要求较高, 不适合大范围搜索。后续会对2种算法进行结合, 在提高搜索效率的同时提高匹配精度; 同时, 针对分辨率与匹配误差间的定量关系及算法的进一步优化改进, 将结合木兰湖实测水深数据开展细致深入的研究分析。
[1] Deng Z L, Ge Y T, Guan W G, et al. Underwater Map-matching Aided Inertial Navigation System Based on Multi-geophysical Information[J]. Frontiers of Electrical and Electronic Engineering in China, 2010, 5(4): 496-500.
[2] Wadhams P. The Use of Autonomous Underwater Vehicles to Map the Variability of Under-ice Topography[J]. Ocean Dynamics, 2012, 62(3): 439-447.
[3] 张静远, 谌剑, 李恒, 等. 水下地形辅助导航技术的研究与应用进展[J]. 国防科技大学学报, 2015, 37(3): 128-135.Zhang Jing-yuan, Shen Jian, Li Heng, et al. Research and Application Progress on Underwater Terrain-aided Navigation Technology[J]. Journal of National University of Defense Technology, 2015, 37(3): 128-135.
[4] 朱华勇, 沈林成, 常文森.基于地形差分矩的TERCOM地图性能估计[J]. 国防科技大学学报, 2000, 22(4): 98-101.Zhu Hua-yong, Shen Lin-cheng, Chang Wen-sen. Estimating the Performance of TERCOM Map Based on Moment of Terrain Difference[J]. Journal of National University of Defense Technology, 2000, 22(4): 98-101.
[5] 马昕, 袁信. 地形辅助惯性导航系统研究[J]. 南京航空航天大学学报, 1997, 29(3): 289-294.Ma Xin, Yuan Xin. Research on Terrain-Aided Navigation System[J]. Journal of Nanjing University of Aeronautics &Astronautics, 1997, 29(3): 289-294.
[6] Hollowell J.Heli /SITAN: A Terrain Referenced Navigation Algorithm for Helicopters[C]//IEEE Position, Location, and Navigation Symposium 1990(PLANS’90). Las Vegas, USA: IEEE, 1990: 616-625.
[7] Bergman N. Recursive Bayesian Estimation Navigation and Tracking Applications[D]. Linkoping: Linkoping University, 1999.
[8] Karlsson T. Terrain Aided Underwater Navigation Using Bayesian Statistics[D]. Linkoping: Linkoping University, 2005.
[9] Yingrong X. Terrain Aided Navigation[D]. Stockholm: Royal Institute of Technology, 2005.
[10] Anonsen K, Hallingstad O, Hagen, et al. Terrain Aided AUV Navigation——a Comparison of the Point Mass Filter and Terrain Contour Matching Algorithms[C]//UDT Europe 2005 Conference Proceedings. Amsterdam: UDT, 2005: 1-10.
[11] Meduna D, Rock S, Mcewen R. AUV Terrain Relative Navigation Using Coarse Maps[C]//Proceedings of the 2009 Unmanned Untethered Submersible Technology Conference. Durham: University of New Hampshire, 2009: 1-11.
[12] 谌剑, 张静远, 查峰. 变分辨率质点滤波水下地形匹配算法[J]. 中国惯性技术学报, 2012, 20(6): 694-699.Shen Jian, Zhang Jing-yuan, Zha Feng. Alterable Resolution Point-mass Filter Algorithm for Underwater Terrain Matching Method[J]. Journal of Chinese Inertial Technology, 2012, 20(6): 694-699.
[13] 刘洪, 高永琪, 张毅. 基于质点滤波的水下地形匹配算法分析[J]. 弹箭与制导学报, 2013, 33(3): 12-16.Liu Hong, Gao Yong-qi, Zhang Yi. The Analysis on Underwater Terrain Matching Algorithm Based on Point-mass Filter[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2013, 33(3): 12-16.
[14] 高永琪, 刘洪, 张毅. 测量误差对水下地形匹配性能的影响研究[J]. 弹箭与制导学报, 2014, 34(1): 180-183.Gao Yong-qi, Liu Hong, Zhang Yi. The Study on Measurement Errors about Underwater Terrain Matching Performance[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(1): 180-183.
[15] 邹炜, 孙玉臣. 水下地形匹配辅助导航技术研究[J]. 舰船电子工程, 2017, 37(8): 5-10.Zou Wei, Sun Yu-chen. Summary of Underwater Terrain Matching Aided Navigation Technology[J]. Ship Electronic Engineering, 2017, 37(8): 5-10.
Analysis on Performance of Underwater Terrain Aided Navigation Using PMF Algorithm
XU Zhen-yang, ZHANG Jing-yuan, WANG Peng, WANG Xin-peng
(College of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China)
Aiming at the problem that the performance of underwater terrain aided navigation is affected by many factors so that best performance cannot be obtained, an underwater digital map with corresponding resolution is made via bilinear interpolation method, and the point-mass filter(PMF) algorithm based on direct probability criterion is adopted to simulate the effects such as speed, depth error, heading error, speed error, initial positional deviation, and underwater topographical features on the navigation performance for undersea vehicle. And the application performance of the PMF algorithm under complex conditions is analyzed. Simulation results show that: 1) the PMF matching algorithm has strong stability under complex conditions; 2) within a certain range, the algorithm shows better resistance to speed and heading errors, but the matching performance will seriously degrade if the speed is too low; 3) the algorithm is greatly affected by the depth error and the initial position deviation, and it needs relatively high requirements for sounding accuracy and inertial navigation system; 4) the algorithm has strong terrain adaptability, and rich terrain is more conducive to matching navigation; and 5) proper selection of the application parameters can effectively reduce the matching error and improve the navigation performance.
undersea vehicle; terrain aided navigation; digital map; point-mass filter (PMF) algorithm; navigation performance
TJ630.33; U666.1
A
2096-3920(2019)06-0614-10
10.11993/j.issn.2096-3920.2019.06.003
徐振烊, 张静远, 王鹏, 等. 基于PMF算法的水下地形辅助导航性能研究[J]. 水下无人系统学报, 2019, 27(6): 614-623.
2019-03-15;
2019-04-04.
国防十三五预研项目(3020603030404).
徐振烊(1994-), 男, 在读硕士, 主要研究方向为武器系统运用与保障工程.
(责任编辑: 许 妍)

