基于SPSS数据分析的服装号型设计

刘睿智， 赵守香

( 北京工商大学 计算机与信息工程学院，北京 100048)

中国是最大的服装生产国、销售国和出口国，世界上每3件服装就有1件来自中国。服装是人们生活中的必需品，关系到其生活质量。服装号型对于服装销售至关重要，服装号型对消费者各种身材和体型覆盖率越大则越有利于产品的销售。虽然我国出台了相关的号型标准，但都是推荐性标准，生产企业在此基础上建立了自己的号型结构体系，并且不同地区、不同年龄的消费者身材体型不尽相同，需要生产企业深入调研设计号型标准。SPSS软件是一款强大的数据分析软件，利用它可以简明、快速、准确地确定号型分类及设置。文中以陕西地区男式上衣为研究对象，具体讨论如何利用SPSS进行大数据分析，精确设计服装号型。

1 样本选取与数据采集

样本量的确定是数据统计的基础。采集数据量过大会费时费力，数据量过小容易产生较大误差，科学合理的样本量对统计分析预测至关重要。采用简单随机抽样方法，按下面公式进行计算：

式中:N为样本容量；Z为置信水平下的统计量；S为总体标准差；d为允许误差。成年人体各控制部位尺寸可接受的误差和标准差见表1[1]。95%置信水平下Z统计量为1.96，选取最大的S/d值6.70，经计算N为172。随机抽取了172名成年男子并测量获取到了他们的体型信息。

表1 人体各控制部位的数值

2 数据预处理

在数据采集过程中难免会出现偏差，造成数据的失真，因此需要对这些数据进行奇异值的检查和处理，剔除一些异常数据以保证结果准确。在进行统计分析时，许多分析方法要求数据符合某种概率分布，大多数方法要求符合正态分布，因此还需要进行正态分布检验。

检查是否存在奇异值主要有两种方法,分别是茎叶图和箱图，具体如图1所示。茎叶图可以看出奇异值的数量，箱图可以找到奇异值的位置，文中将两种方法组合运用，以增强数据的准确性。在茎叶图中，显示了整体身高变量的频数、茎和叶[2]。茎表示数值的整体部分，叶表示数值的小数部分，“≥186”表示身高变量数据中存在一个奇异值。从箱图中可以看出，107号是奇异值，该奇异值是由于身高过高导致的，因此将107号样本数据剔除。按照该方法对其他变量进行检验，将样本中4个奇异值剔除，最终样本数量为168个。

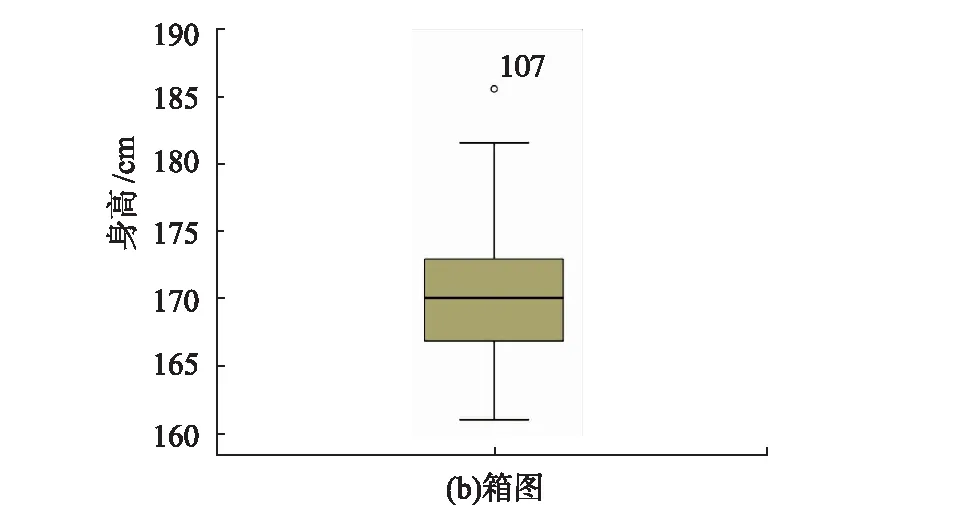
图1 检查奇异值的两种方法Fig.1 Two ways to cheek singular values

正态分布检验常用的方法是P-P概率图和Q-Q概率图，其中P-P概率图简单直观、便于判断，因此文中采用该方法对身高变量进行正态分布检验，检验结果如图2所示。由图2可以看出，样本数据大致聚集在一条直线上，可以认定身高变量基本符合正态分布，且各点是无规则的即样本是随机的。同理可得，其他变量也基本遵循正态分布。

图2 身高及身高去趋势的正态P-P分布 Fig.2 Height and height trending normal P-P diagrom

3 数据的基本分析

3.1 描述性分析

文中选取最大值、最小值、平均值及标准差等具有代表性的指标进行分析，分析结果见表2。

表2 变量统计性描述

由表2可以看出，陕西地区成年男子身高、体质量、胸围方差较大，表示个体在这些变量上存在着很大差异，其他变量差异性较小。

3.2 相关性分析

相关性分析是研究变量之间关系密切程度常用的方法之一。变量间的相关程度可以用相关系数衡量。相关系数用r表示，正态分布的等间隔测度变量x与y间的相关系数采用Pearson 积矩相关公式计算：

表3为各变量间相关系数矩阵。由表3可以得出：所有变量均呈正相关关系。其中，身高与体质量、全臂长之间存在中度相关或高度相关；胸围与肩宽、后背长、颈围存在中度相关或高度相关；其他变量之间也存在中度相关及低度相关。相关性分析是进行回归分析、建立回归模型的重要依据，相关性越强，线性回归模型效果越好。

表3 变量间相关系数矩阵

3.3 因子分析

因子分析的目的是从众多变量中挑选出一个或几个具有代表性的变量[3]，因此因子分析的前提条件是变量之间存在较强的相关关系。在因子分析前需要检验变量间是否满足较强相关关系，常用的检验方法有KMO检验和Bartlett球形度检验。KMO检验统计量用于比较变量间简单相关系数和偏相关系数的指标，计算公式为

式中：rij为变量xi和其他变量xj间的简单相关系数；pij为变量xi和其他变量xj间在控制剩余变量下的偏相关系数。KMO取值范围在0～1之间，当所有变量间简单相关系数平方和大于偏相关系数平方和时，KMO接近于1，变量间的相关性强，适合进行因子分析。文中运用KMO和Bartlett球形度检验对样本数据进行测试，具体结果见表4。Bartlett球形度检验的统计量根据相关系数矩阵的行列式计算得到，若变量观测值较大且对应的p值小于给定的显著性水平α，认为原有变量适合进行因子分析。由表4可以看出，KMO值为0.832，较接近于1，说明适合进行因子分析；同时，Bartlett球形度检验中显著性接近于0，显著性水平α为0.05，0小于显著性水平α，适合进行因子分析。因此，两种检验方法均证明变量间适合进行因子分析。

表4 KMO 和Bartlett检验结果

总方差解释见表5。表5中初始特征值列反映了因子分析初始解的情况，第1个因子的特征值为4.531，解释原有7个变量总方差的64.732%，累计方差贡献率64.732%；第2个因子的特征值为1.509，解释原有7个变量总方差的21.560%，累计方差贡献率86.283%，其余数据含义类似，初始解中提取了7个因子，原有变量总方差均被解释，累计方差贡献率100%。提取载荷平方和列描述了因子解的情况，由于指定提取2个因子，它们共解释了原有变量总方差的86.283%，整体上，原有变量信息丢失较少，因子分析效果较理想；旋转载荷平方和列描述了最终因子解情况，因子旋转后累计方差贡献率没有发生变化，但重新分配了各个因子解释原有变量的方差，使得因子更易于解释。

表5 总方差解释

注：提取方法为主成分分析法。

图3为因子分析碎石图。

图3 因子分析碎石图Fig.3 Gravel map

由图3可以看出，第1个因子的特征值很高，对解释原有变量的贡献最大；第3个因子以后的特征值都较小，对解释原有变量的贡献很小，因此提取两个因子是合适的。

旋转后的成分矩阵见表6。由表6可以看出，第1个因子主要解释了总肩宽、胸围、后背长和颈围这几个变量，身高、全臂长和体质量主要由第2个因子解释。

4 聚类分析

聚类分析是将样本数据按照一定的规则进行分类，同类样本具有较大的相似度，不同类样本之间存在着较大差异。K-means均值聚类方法具有思想简单、易于理解、容易实现、处理速度快、占用内存少等优点，适合大样本聚类，分类效果较好[4]，因此文中采用此方法对体型数据进行聚类分析。聚类分析的核心步骤是：确定聚类数目；确定初始类中心点；确定样本点到中心点的欧氏距离，完成一次迭代过程；重新确定中心点并重复以上步骤，直至迭代终止。

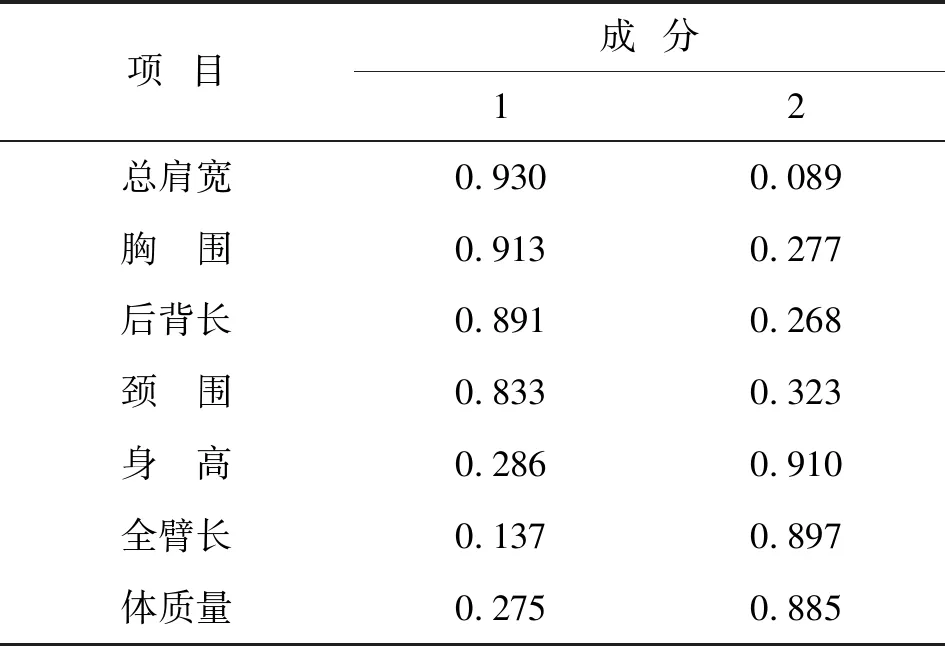
表6 旋转后的成分矩阵

注：提取方法为主成分分析法； 旋转方法为凯撒正态化最大方差法；旋转在 3 次迭代后已收敛。

4.1 聚类变量的确定

通过体型的特征指标确定聚类变量，特征指标包括身体的不同部位，即身高、体质量、胸围等[5]。通过因子分析可知，在两个因子中都存在着具有代表性的变量，通过计算因子中相关指数，找出相关指数最大的变量作为控制变量即聚类变量，相关指数计算公式为

式中：i=1,2,…,m，m为所在类的指标个数；rij为相关系数，i≠j，j=1,2,…,m。计算结果见表7。

表7 因子相关指数

4.2 聚类结果分析

将身高和胸围作为聚类变量,按照K-means均值聚类方法对样本数据进行分类。考虑到服装生产的实际，服装号型设置不宜过多，因此3～5类最为合理。经过比较分析，发现聚类数为3时分类结果最清晰，效果最好，最终聚类中心见表8。由表8可以看出，不同类别个案数及所占比例中间多、两边较少，表明聚类结果合理。胸围的聚类中心大致为86，93，99，身高为166，171，177，参考国家号型标准同时兼顾分析结果，将相邻体型之间的胸围差设置为4，身高差设置为5，结果清晰均匀。

表8 最终聚类中心

Tab.8 Final cluster center

项目聚类123胸围85.992.698.8身高166.4170.6177.1个案数578922比例345313

4.3 中间体数值的确定

将不同类别样本数据分离出来，分别计算不同变量的平均值，作为中间体数值，具体结果见表9。中间体具有一定的代表性，反映了不同分类样本的体型特点:M表示体型样本身高较低，胸围较小；N表示体型样本频率最大，表明此体型人数最多，体型中等；P为体型样本身高较高，身材健壮[6]。为便于表示体型，将表8中1体型用M表示，2体型用N表示，3体型用P表示。如果按照表9中的数值进行服装号型的推算，必然会带来许多不便，因此需要对其进行圆整，圆整后结果见表10。

表9 平均值

Tab.9 Average value

项目MNP身高166.417170.587177.064体质量59.06362.77369.573胸围85.89592.55298.773颈围38.07440.15341.586总肩宽43.97047.01349.586后背长41.50544.36846.341全臂长54.60255.84557.177

表10 圆整后平均值

Tab.10 Rounded average

项目MNP身高166171177体质量596369胸围869399颈围384042总肩宽444750后背长424446全臂长555657

4.4 各部位档差的设置

档差的设置是为了便于号型的制定。档差设置时，不仅要考虑顾客的舒适性，还要便于企业生产，档差设置太大不能满足众多的消费者需求，档差设置太小则不利于生产者批量化生产。文中利用回归方程设置各部位档差。胸围在第1个因子中具有代表性，因此其他变量用胸围来描述，同理第2个因子用身高表示。在不同体型样本中，分别建立身高与体质量、全臂长的线性关系，胸围与颈围、总肩宽、后背长之间的线性关系[7]。身高用H表示，胸围用B表示，线性关系见表11。

表11 线性回归方程

首先设置身高和胸围的档差分别是5和4，将其代入不同部位的线性回归方程可以得到相应的档差。为便于生产，将3类体型不同档差进行统一化，得到了最终确定的档差，具体结果见表12。由表12可以看出，颈围和总肩宽档差大于国家标准中规定的数值(颈围档差为1，总肩宽为1.2)，这充分体现了陕西男子的体型特征，身材中等，肩宽颈粗的特点，这与陕西男子的体型特征相一致。

表12 档差设置

注：括号外为计算值，括号内为采用值。

4.5 确定不同号型具体数值

在计算不同号型具体数值时，首先要统计分析不同体型各部位的最大值和最小值，然后结合中间体、档差、最大值、最小值和线性方程综合考虑数值的设置。以体型N为例，首先统计各部位最大值和最小值，具体见表13；再按照中间体及档差设置数值；最后根据最值和线性方程进行调整修正，最终号型划分结果见表14[8]。同理，按照此步骤对M和P体型部位数值进行设置。

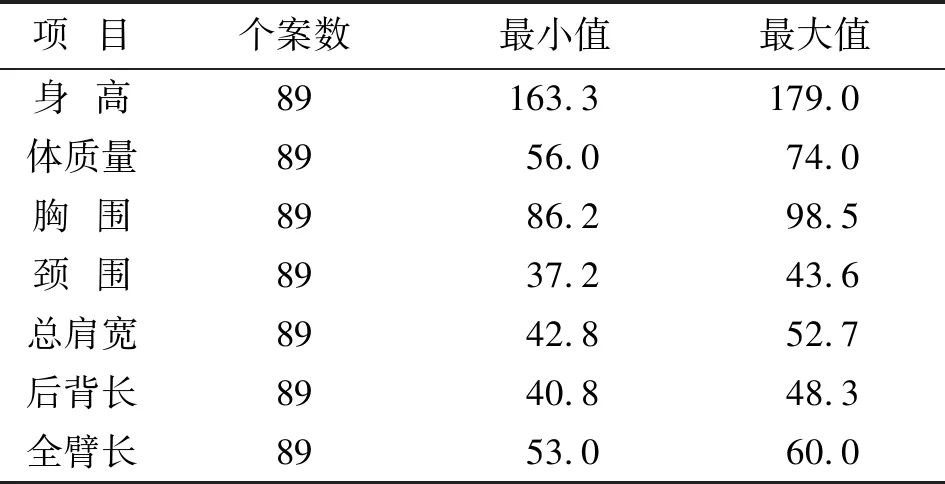
表13 N体型变量统计描述

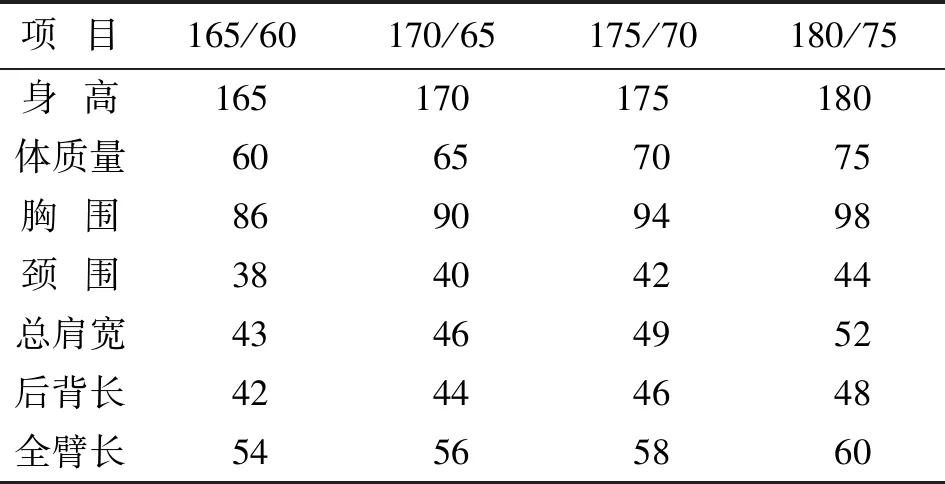
表14 N体型下的号型设置

5 结语

号型设置是否合理对于服装生产和销售至关重要。利用SPSS数据分析软件并根据随机样本数据信息可以快速、准确地构建服装号型体系，方便生产企业根据不同地域、不同年龄的目标客户建立合理的号型标准[9]。利用陕西地区男子身材体型数据信息，结合SPSS数据分析工具，划分了N，M，P 3种体型，并在每种体型下设置了相关号型及不同号型的数据特征，为服装设计及生产提供参考与借鉴。