冲击载荷下TC18钛合金力学性能模拟研究
贾宝华,王丹丹,李 革,顾永强
(内蒙古科技大学,内蒙古 包头 014010)
0 引 言
TC18钛合金具有淬透性、锻透性、塑性好的特点,近些年作为承力件被广泛应用于航空航天等高科技领域。在实际使用中,承力件不可避免的要承受冲击载荷作用[1],因此对TC18钛合金进行动态力学性能方面的研究十分必要。由于TC18钛合金在准静态下的强度非常高,再加上材料的应变速率效应,进行动态力学性能试验比较困难,可优先考虑采用数值模拟方法进行研究。数值模拟结果的精确性主要取决于合金本构方程的精确性。当采用ABAQUS软件进行冲击载荷下的动态力学性能模拟时,仅可使用经典的J-C模型。该模型适用于描述大多数金属材料的动态力学性能,具有良好的通用性。在常温下,J-C模型的应变速率强化项采用了较为简单的对数关系,即认为流动应力与应变速率的对数呈线性关系[2]。高应变速率会使塑性变形阶段的本构关系表达式产生较大误差。另外在整个动态力学响应过程中,不同材料会呈现出不同的微观结构变化,统一采用经典的J-C模型时,其精确性较差。
根据以往研究,大多数金属材料属于应变速率敏感材料,在高应变速率和准静态下的力学性能截然不同[3-4]。近年来,国内很多学者针对金属材料的动态力学性能进行了试验研究[5-6]。Ran等[7]采用分离式Hopkinson压杆技术,对Ti-55511合金在350~2 900 s-1等应变速率下进行了室温动态压缩试验,结果表明:Ti-55511合金的应变速率硬化效应和应变速率敏感性显著,在高应变速率加载条件下形成脆性剪切带。秦建峰等[8]采用分离式霍普金森压杆对TC4钛合金热氧化后的冲击性能进行了研究。结果表明,热氧化使得 TC4钛合金具有较好的静态力学性能和较高的应变速率强化效应;用修正后的J-C模型对其进行实验数据拟合,能更好地表征其力学性能。张长清等[9]采用分离式霍普金森压杆对TC4-DT钛合金进行动态压缩试验,得到真实应力-应变曲线,使用改进的J-C本构模型拟合实验数据,得到该材料室温下的动态塑性本构方程,对比模拟结果和实验数据,证明该本构模型可以更精确可靠地预测TC4-DT钛合金高应变速率下的塑性流变应力。陈小翠等[10]为了更高精度地模拟高应变速率下金属材料的局部变形特征,在混合有限元的基础上,基于有限元分析程序重新编写了新单元,计算精度明显提高。
综上所述,对金属材料的冲击性能研究十分必要。由于试验研究难度大,耗资多,载荷作用时间极短,对仪器精度和采集速度要求很高,尤其对于TC18钛合金这类高强度材料,试验研究难度更大。有限元分析(finite element analysis, FEA)利用数学近似的方法对真实物理系统(几何和载荷工况)进行模拟,操作简单,可以方便地实现更高应变速率下的动态力学性能研究。
为了更精确地实现高强度金属材料更高应变速率下的数值模拟,以TC18钛合金试验数据为基础,在J-C模型的基础上做了调整,利用ABAQUS软件的子程序接口自定义了材料本构子程序UMAT,以代码的形式来扩展ABAQUS程序的功能。通过与ABAQUS/Standard软件分析结果以及实验结果的对比,验证自定义材料本构子程序UMAT计算结果的精确性与可靠性。
1 UMAT用户材料子程序
1.1 实验
在常温状态下,采用分离式霍普金森压杆(SHPB)装置对TC18钛合金试件进行高应变速率(500、1 000、1 500 s-1)下动态压缩实验。试件为φ6 mm×6 mm的圆柱体。在入射杆和透射杆上贴有应变片,对实验数据进行采集和存储。
1.2 冲击载荷下TC18钛合金本构方程
用J-C模型模拟TC18钛合金受冲击载荷的应力σ,如式(1)所示。
(1)
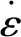

(2)
为了提高拟合精度,也为给其他材料的冲击模拟提供更为合理的本构方程,对经典的J-C本构方程加以调整,使得应变速率和应变耦合效应更加精确,具体如式(3)。

(3)
式中:D、E、F为常数,可由实验数据拟合得出。
基于调整后的J-C本构方程(式3),对TC18钛合金在常温冲击载荷下的实验数据进行精细拟合。其应力-应变关系描述如式(4)。
σ=(1 060-6 882.3ε2+3 094.3ε-1.652)×
(4)
1.3 应力更新算法
将修正的J-C方程应用于应力更新算法,基于Von-Mises屈服面,采用J2流动法则,使塑性流动沿着屈服面的法线方向进行。为了避免显示积分算法的误差累积以及不稳定性,采用完全隐式的积分算法。
首先给定一个弹性预测步,在弹性预测阶段,塑性应变保持不变。之后塑性调整步返回至更新屈服面上,总体应变和塑性流动方向在塑性修正阶段保持不变。
(5)
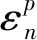
(6)
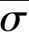
(7)
式中:G为剪切模量。用牛顿迭代法调整参数,至屈服函数无尽趋近于0,即满足屈服准则时迭代过程终止。
(8)
(9)
这样,塑性应变、内变量和塑性参数更新为方程组(10)。
(10)
Δλn+1=Δλn+δλn
1.4 材料雅克比矩阵
在完全隐式的积分算法中,会用到材料雅克比矩阵来求解平衡方程,用DDSDDE矩阵来表示。
λ*和μ为拉梅常数,可以用弹性模量E和泊松比υ来表示它们。
(11)
(12)
1.5 UMAT子程序流程
基于上述的应力更新算法和一致切线刚度矩阵,ABAQUS软件主程序在增量步开始时在积分点上调用UMAT子程序,UMAT子程序流程图如图1所示。

图1 UMAT子程序计算流程图Fig.1 Computational flow diagram of UMAT subroutine
2 模型的建立
2.1 有限元模型的建立
压缩试件模型为φ6 mm×6 mm的圆柱体。入射杆和透射杆均简化为φ25 mm×1 000 mm的圆柱体。模型的几何尺寸、载荷及其约束均关于中心轴线对称,故选用二维轴对称单元。对称轴设置为对称性边界条件;压杆和试件之间的接触设置为光滑无摩擦的硬接触;透射杆末端设置固定约束;在压杆接触试件的杆端做了网格加密。图2为TC18钛合金试件受冲击时的二维有限元模型图。
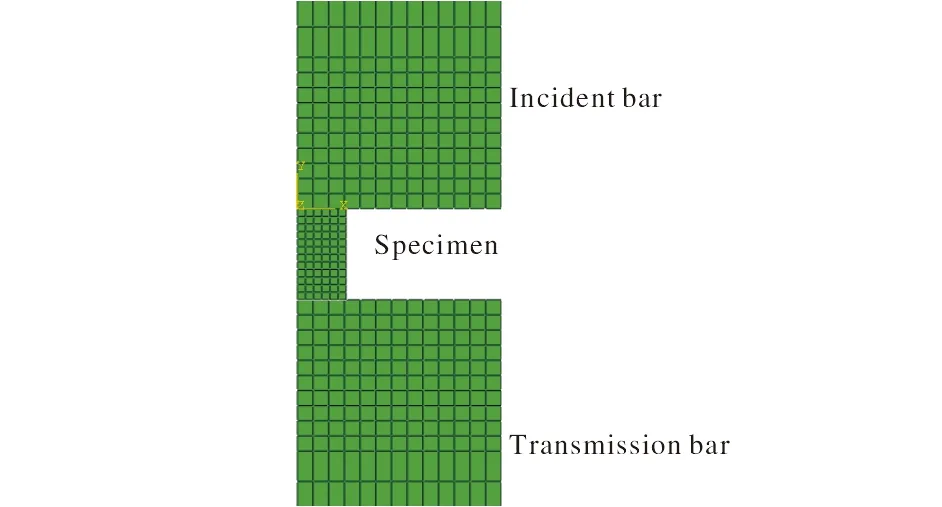
图2 TC18钛合金试件受冲击时的二维有限元模型Fig.2 Two-dimensional finite element model diagram of TC18 titanium alloy specimen under impact loads
2.2 材料参数
模拟过程中的模型信息如表1所示。入射杆和透射杆的材料参数如表2所示。在使用经典的J-C本构方程计算时,TC18钛合金试件的材料参数如表3所示。在使用UMAT子程序计算时,UMAT子程序中一共设有10个材料常数组成PROPS数组,物理含义如表4所示。并申请一个13维的存储状态变量矩阵,其中1~6为弹性应变,7~12为塑性应变,13为塑性应变速率。
表1模型信息
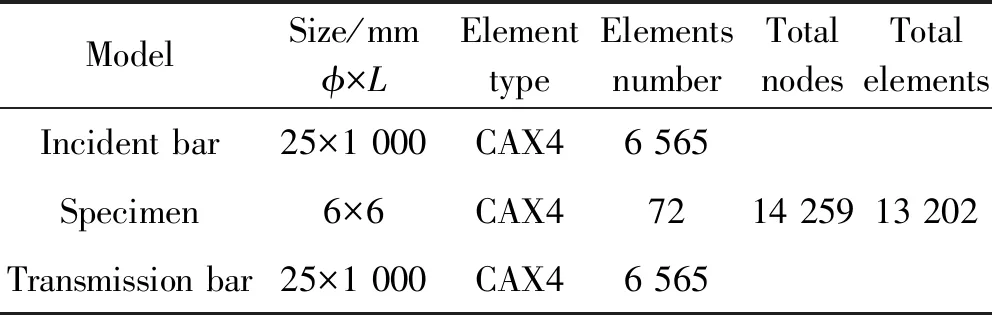
Table 1 Model information
表2入射杆和透射杆的材料参数

Table 2 Material parameters of incident and transmission bar
表3TC18钛合金试件的材料参数

Table 3 Material parameters of TC18 titanium alloy specimen
表4UMAT子程序的材料参数

Table 4 Material parameters of UMAT subroutine
2.3 施加载荷
为了简化模型,模拟过程中用入射杆端部施加冲击载荷速度来代替撞击杆的应力脉冲作用。冲击载荷速度与应变速率的关系如下:
(13)
式中:L为试件长度;V1(t)、V2(t)分别为试件入力端和出力端的速度。模拟过程中,在应变速率为500、1 000、1 500 s-1时,冲击速度分别为4 500、5 750、7 000 mm/s。
3 结果与分析
使用ABAQUS软件模拟了应变速率为500、1 000、1 500 s-1时TC18钛合金的受力情况。对比分析了在相同边界条件及相同载荷条件下,UMAT子程序的计算结果、ABAQUS软件自带本构模型计算结果和实验数据。
3.1 应变速率分析
为了验证ABAQUS/Standard软件结合UMAT子程序计算的正确性,输出应变和时间的数据,拟合求导得到应变速率进行验证,如图3所示。由图3可以看出,在冲击速度为4 500、5 750、7 000 mm/s时,应变速率均十分接近500、1 000、1 500 s-1。由此验证UMAT子程序和模型的正确性。
3.2 应力-应变曲线分析
为了进一步验证UMAT子程序的精确性,将 ABAQUS/Standard软件结合 UMAT子程序进行应变速率分别为500、1 000、1 500 s-1的有限元模拟。在相同模型、接触条件及载荷下,使用ABAQUS软件自带本构模型进行模拟计算。图4为TC18钛合金试件在应变速率500、1 000、1 500 s-1下的UMAT计算数据和ABAQUS自带本构模型计算数据和实验数据的对比图。从图4可以看出, UMAT子程序计算的应力-应变分布曲线更接近实验数据。
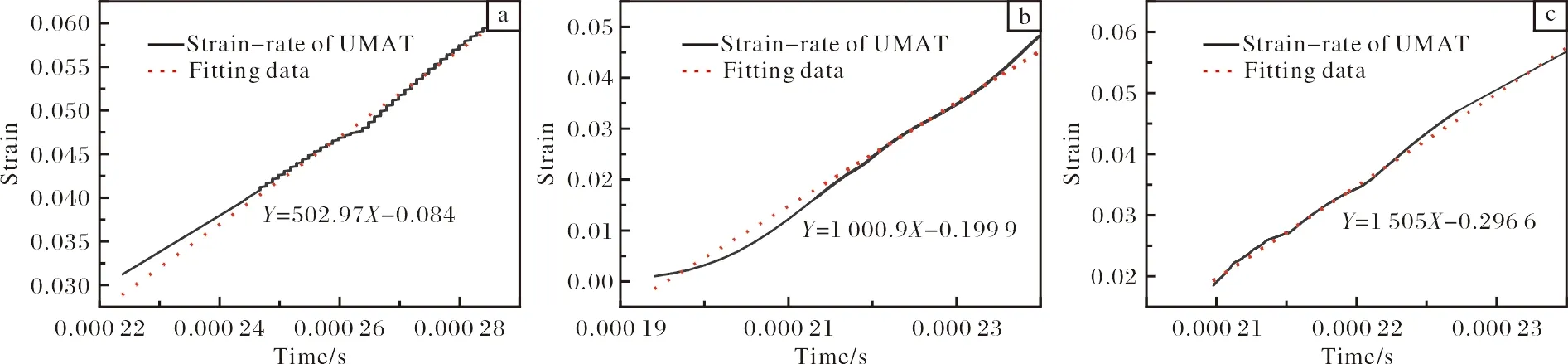
图3 UMAT子程序拟合的不同冲击速度下应变速率曲线Fig.3 Strain rate curves fitted by UMAT subroutine under different impact velocities: (a)4 500 mm/s; (b)5 750 mm/s; (c)7 000 mm/s
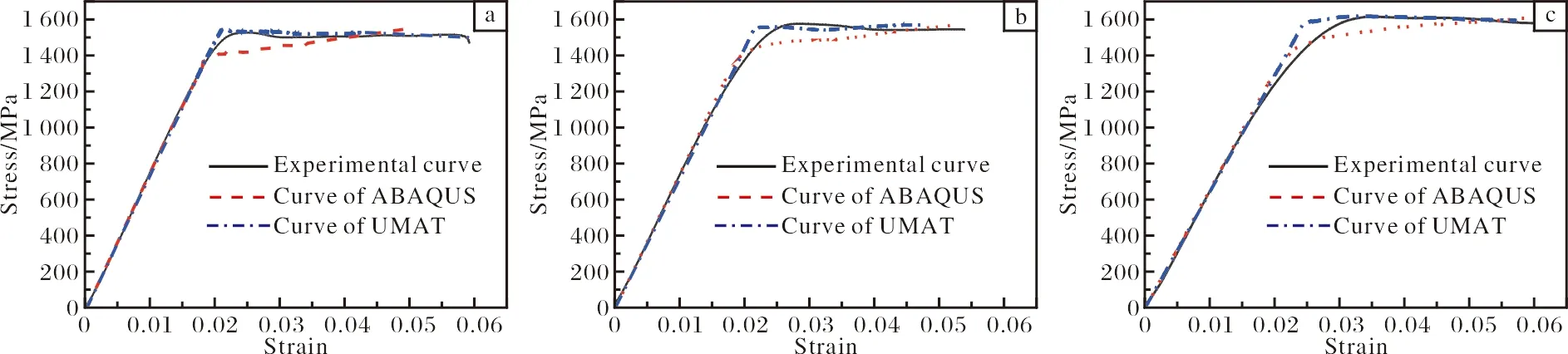
图4 不同方法得到的不同应变速率下应力-应变数据对比图Fig.4 Comparison of stress-strain data obtained by different methods under different strain rates: (a)500 s-1; (b)1 000 s-1; (c)1 500 s-1
图4比较直观地表明了UMAT子程序的计算结果相比ABAQUS软件更精确。为了定量地证明上述结论,引入统计分析参数平均相对误差绝对值AARE来表征,其数学表达式如下。
(14)
式中:N为流变应力数据点的个数;Ei表示流变应力的实验值;Pi表示流变应力值的模拟值。分别将由2个本构模型计算的流变应力值代入式(14),得到各自的平均相对误差绝对值,如表5所示。由表5可看出,在应变速率为500、1 000、1 500 s-1下,由UMAT子程序模拟的平均相对误差绝对值均低于ABAQUS软件自带本构模型进行模拟的平均相对误差绝对值。
表5UMAT子程序和ABAQUS软件在不同应变速率下的平均相对误差绝对值(%)
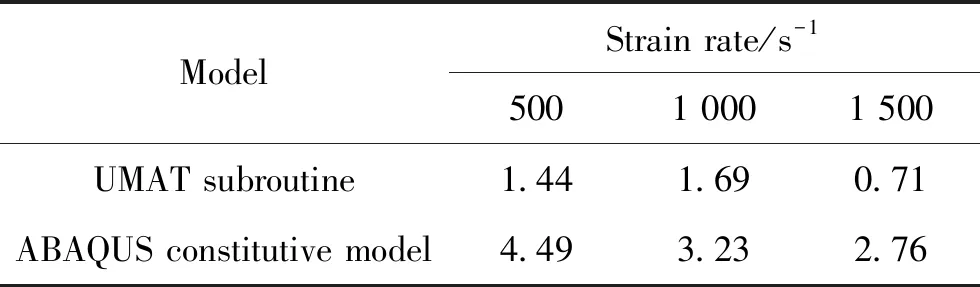
Table 5 Average absolute value of relative error under different strain rates obtained by UMAT subroutine and ABAQUS software
综上,从定性和定量2方面均表明本研究开发的UMAT子程序相比ABAQUS软件自带模型具有更高的模拟计算精度,能够更准确地反应TC18钛合金在冲击载荷下的力学性能,从而为TC18钛合金的力学性能仿真计算奠定基础。
3.3 嵌入UMAT后应力云图分析
基于以上对模型和子程序的验证,嵌入UMAT子程序计算结束时,提取不同应变速率下TC18钛合金的应力云图。图5分别取自应变速率500、1 000、1 500 s-1下计算结束时刻的应力分布云图。由图5可见,TC18钛合金试件的应力云图呈现均匀的红色,说明应力分布均匀,Mises应力分布相差不超过1 MPa,该精度十分可靠[11]。另外,随着应变速率的增大,应力最大值随之增加,应变速率为1 500 s-1时最大应力达到1 615 MPa。
4 结 论
(1)经过对J-C模型的修正,利用ABAQUS软件重新定义材料子程序UMAT。修正后的J-C本构模型嵌入UMAT子程序后,计算结果相比常规的ABAQUS模拟结果更精确。

图5 TC18钛合金在不同应变速率下的应力云图Fig.5 Stress contours of TC18 titanium alloy under different strain rates: (a)500 s-1; (b)1 000 s-1; (c)1 500 s-1
(2)通过对TC18钛合金在不同应变速率下的应力云图进行分析,表明试件上的应力分布均匀,符合理论预期,并且应力最大值随着应变速率的增加而增大。
在实际工作中,TC18钛合金构件除了承受高应变速率冲击载荷,还可能同时承受高温载荷的作用。今后将进一步考虑对高温及高应变速率共同作用下的TC18钛合金动态力学性能进行模拟程序的二次开发。

