粗颗粒填料蠕变的缩尺效应研究

马 捷，韩文喜，2，聂 超

(1.成都理工大学环境与土木工程学院，四川成都610059；2.地质灾害防治与地质环境保护国家重点实验室，四川成都610059)

0 引 言

在我国西南地区，许多地基建设的形式为高填方，而填料在高填方工程中起到了十分重要的载体作用。高填方工程往往具有岩土种类多、填方量巨大等特点，且有些工程所在地地质条件十分复杂[1-3]。而粗颗粒土作为许多填方工程的主要填料，其力学特性直接关系到填方体的变形和稳定性[4]。目前，很多实际工程现场案例反映出填筑体存在沉降问题，需要进一步的探究分析。而对于粗颗粒填料的填筑体沉降计算问题，学界尚未形成一个成熟的体系[5- 8]。这是因为岩土体复杂多变的特性，加之复杂的地形因素的影响，故而分析岩土体在自重作用时的沉降问题变得比较困难。由于粗颗粒填料既不同于土，又不同于岩石，故其变形机理尚不明确，往往属于弹塑性或粘弹性的问题范畴[9-11]。

本文针对高填方粗颗粒填料蠕变的缩尺效应问题进行研究。以灰岩质粗颗粒土为试验研究对象，对贵州某高填方工程填料的级配进行了3次缩尺，形成了3组最大粒径不同的相似级配；之后，通过击实试验确定3种缩尺级配试样的最大干密度，研究总结了粗颗粒土最大干密度与级配缩尺比的关系；然后对3种缩尺试样分别进行对应尺寸的单轴侧限压缩试验；最后，对3组侧限压缩蠕变试验的结果选择了合理的经验公式，描述了应变-时间的关系，总结了粗颗粒填料最大粒径与其蠕变变形的关系，为后续不同级配填料的蠕变变形提供理论依据。

1 粗粒料蠕变缩尺效应的室内试验

1.1 级配缩尺试验

本次研究采用的填料为灰岩质填料，填料颗粒粒径最大达500 mm。由于室内侧限压缩蠕变试验最大粒径可达200 mm，本文同样采用灰岩对其缩尺效应进行研究。缩尺后的级配见表1。表1中，试样D1所含有的最大粒径为200 mm，试样直径为1 000 m；试样D2所含有的最大粒径为60 mm，试样直径为300 mm；试样D3所含有的最大粒径为40 mm，试样直径为200 mm。对原级配进行以上3次缩尺，然后进行蠕变试验研究。

表1 试样级配

按下式计算每组试样的不均匀系数Cu与曲率系数Cc，即

(1)

(2)

式中，d60为限制粒径，即小于该粒径的土粒质量为总土粒质量的60%；d30为中值粒径，即小于该粒径的土粒质量为总土粒质量的30%；d10为有效粒径，即小于该粒径的土粒质量为总土粒质量的10%。计算结果汇总至表2。

表2 不同试样级配特征值

1.2 室内击实试验

试样的密实度对后续的侧限压缩试验有重要的影响。这是因为在侧限压缩试验中，由于试样受竖直向下的应力，其密实度影响着试样产生的沉降量。因此，试样的密实度不同，可能会导致不同的试验结果。本次试验采取重型击实法击实，测得3种缩尺级配试样的最大干密度，见表3。

表3 不同最大粒径所对应的最大干密度

从表3可以看出，试样最大干密度与最大粒径呈近似线性正相关关系。通过上述试验，可以确定相似级配法缩尺后的试样的最大干密度。为了统一密实度，避免压实度差异对侧限压缩试验结果产生影响，基于实际填方工程中的填料压实度，确定了侧限压缩试验中的试样的压实度为93%，试样D1的密度为2.015 g/cm3；试样D2的密度为1.97 g/cm3；试样D3的密度为1.96 g/cm3。

1.3 3种缩尺试样模型的侧限压缩蠕变试验

(1)准备制样。将灰岩质填料筛分，按表1级配进行配比，全部按含水率为0.31%添加水量后进行拌和。

(2)将拌和好的填料分别等分5次，对应装填至大型(直径1 000 mm)、中型(直径300 mm)、小型(直径200 mm)3种不同尺寸的单轴侧限压缩试验仪中，分别加压蠕变，每种试样所加压强都分别为0.34、0.54、0.74 MPa和0.94 MPa。在加压蠕变过程中，按0.1、0.25、1、2.25、4、6.25、9、12.25、16、20.25、25、30.25、36、42.25、60 min时间顺序测量记录试样高度的变化，后每隔1 h测记1次，直到蠕变完成。

(3)稳压0.5 h后，待到单位时间内的蠕变量满足稳定要求(蠕变完成以12 h内位移变化小于0.02 mm为标准)[12]，再升压至下一级压力。

(4)重复加压步骤，直至加压至最后一级压力，直到在这一级压力下达到稳定状态。

表4 压缩指标计算结果

2 数据分析

2.1 侧限压缩蠕变试验

3种不同缩尺级配试样压缩指标计算结果见表4。不同轴向应力σ下，缩尺比与沉降量关系见图1。

图1 不同轴向应力下的缩尺比-沉降量关系

从图1可知，3种不同缩尺级配的试样在不同应力状态下沉降量与缩尺比之间的关系。轴向应力σ=0.34 MPa时，试样的沉降与其缩尺比呈近似正相关关系，且线性相关系数R2=0.997 8>0.9，体现出这一级轴向荷载下试样沉降量与缩尺比之间有着十分良好的线性正相关关系；σ=0.54 MPa时，试样沉降量与缩尺比的线性相关系数R2=0.999 6>0.9，线性关系更加良好；当试样处于0.74 MPa以及0.94 MPa的轴向应力下时，相关系数R2=1，试样沉降量与缩尺比有着严格的线性正相关关系。同时还可以发现，轴向应力越高，试样沉降量与缩尺比关系曲线的斜率越大，同时截距越小。

通过对沉降量—缩尺比曲线的拟合，可建立蠕变量与缩尺比的关系。根据两者之间的线性关系，可以建立如下关系式

S=a×M-b

(3)

式中，S为蠕变变形量；M为缩尺比；a、b为拟合常数。

而通过对试样D1侧限压缩蠕变试验数据分析得出，式(3)可按如下表达

(4)

式中，Es为压缩模量；p、q为常数。本次试验中，p取847.5，q取0.12，按上式对不同缩尺比下试样的沉降量进行反演计算与拟合，计算结果见表5～6。

表5 试样D1缩尺比与沉降量的拟合关系

由表5～6可以看出，试样D1的压缩模量与轴向应力、缩尺比之间有良好的线性关系，通过对D1试样的侧限压缩试验，可得该试样在各个应力状态下试样沉降量与缩尺比的关系。

同理，可以得到试样D2、D3的试验结果，拟合公式模型同式(4)。对于D2，p取1 674.8，q取0.12；对于D3，p取2 238.4，q取0.12。按式(4)对不同缩尺比下试样的沉降量进行反演计算。计算结果见表7～10。

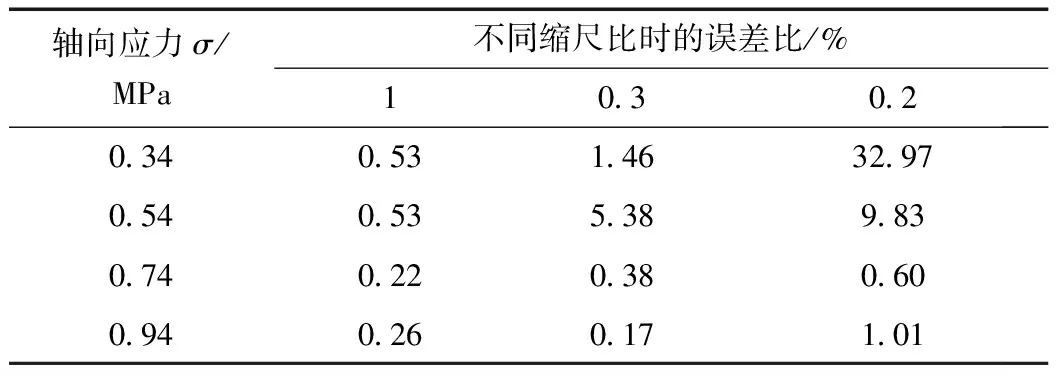
表6 试样D1线性拟合与试验值误差比值

表7 试样D2缩尺比与沉降量的拟合关系

表8 试样D2线性关系与试验值误差比值

表9 试样D3缩尺比与沉降变形量的拟合关系

表10 试样D3线性关系与试验值误差比值

从表7～10可以看出，试样D2、D3的压缩模量、应力状态、缩尺比与蠕变量之间建立的关系同样呈近似线性，但试样D2、D3的线性效果不如试样D1好。因此，在计算压缩模量、应力状态、缩尺比与蠕变量关系式时，取缩尺比较大的试样的参数与实际结果更吻合。

2.2 应力—应变分析

本次研究使用MATLAB拟合出3种试样的应力—应变曲线，与试样的应力—应变曲线对比见图2。在均方根、和方差都趋于0的情况下，得到解释能力与拟合效果最好的拟合方程形式为

(5)

式中，ε为应变；a、b、c为拟合方程参数，3种试样拟合方程参数见表11。

表11 应力—应变曲线拟合参数

图2 3种试样的应力—应变曲线与MATLAB模拟曲线对比

从各试样的应力—应变参数可以看出，当轴向应力越大时，应变的增量越小。且当应力趋于无穷大时，应变趋于不变，即应力-应变曲线有1条水平的渐近线。经过MATLAB软件推算，在轴向应力很大的情况下，试样D1的应变趋于10.05%；试样D2的应变趋于7.34%；试样D3的应变趋于3.58%。由此可以推断，在应力足够大的情况下，在侧限压缩条件下时，粗颗粒土体会成为近似刚体，不再发生压缩变形，此时土体蠕变量完全可以满足要求。同时可以判断应变渐进值与缩尺模量呈正相关关系。

3 结 语

本文通过贵州某高填方工程灰岩质粗颗粒填料的缩尺蠕变试验，研究了粗颗粒填料在压缩蠕变过程中的工程特性与规律，得出以下结论：

(1)试样最大干密度与最大粒径呈近似线性正相关关系。

(2)试样的沉降量与最大粒径呈正相关关系。由此推测，可能是由于最大粒径改变后，粗颗粒填料自身强度发生变化，粗颗粒填料内部颗粒形状差异变大，从而导致沉降量增大。同时，经过试验可得试样经过相似级配法缩尺后，其沉降位移量与缩尺比有着严格的正比关系。

(3)随着轴向应力的增大，粗颗粒土的蠕变将趋于定值，且此渐近值与试样缩尺比呈正相关关系。