基于多迭代变分模态分解与复合多尺度散布熵的生物组织变性识别方法*

胡伟鹏,邹 孝,刘 备,赵新民,钱盛友

(湖南师范大学物理与电子科学学院,长沙 410081)

高强度聚焦超声治疗就是将超声波的能量聚焦于靶区,使靶区内产生高温,利用蛋白质在一定的温度下会产生变性使组织细胞坏死的原理,达到治疗或组织切除目的[1]。在治疗过程中,随着超声波聚焦于靶区,靶区的细胞逐渐失去活性[2],位于超声波传播路径上的正常组织也会吸收超声能量,且越接近靶区的组织吸收的能量越多,因此使用超声治疗中需要实时监测治疗区域情况。迄今为止,超声领域的研究人员已经从超声衰减系数,声速和熵等参数对采集的超声信号进行研究,希望找到能准确反映生物组织特性的参数[3-6]。但采集的超声背散射回波信号含有大量的噪声,对判断生物组织是否变性造成了很大的困难。减少超声背散射信号中的噪声,对准确判断生物组织是否发生变性非常重要。

经验模态分解(Empirical Mode Decomposition,EMD)与变分模态分解(Variational Mode Decomposition,VMD)凭借其强大的分析和去噪能力广泛应用于各个领域[7-11]。但是EMD得到的本征模函数(Intrinsic Mode Function,IMF)存在模态混叠,微弱信号难以提取,容易产生虚假信号[12-13],对于频率相近的分量难以正确分离。与EMD相比VMD的鲁棒性较好[14],在分析频率相近的分量时更加容易分离,但是VMD分解的模态数是一个定值,在分解过程中部分噪声信号会与有用信号分在同一个IMF中。本文基于VMD提出了多迭代变分模态分解(Multi-Iterative Variational Mode Decomposition,MIVMD),MIVMD在计算过程中,计算了各个IMF的能量比,将低能量比的IMF滤除,并根据重构信号中有用频率的能量比进行多次分解重构。

由于超声波在生物组织内的非线性传播特性,实验采集的超声背散射信号是一种非线性信号[15]。信号的复杂程度会根据生物组织变性程度的改变而改变。目前为止,我们通常通过计算信号的熵值来评估信号的复杂程度[16-18]。散布熵(Dispersion Entropy,DE)是一种新的评估时间序列动态特征的参数,DE不会产生未定义的熵值,且时间序列的微小改变不会对DE造成很大影响[19]。复合多尺度散布熵(Composite Multi-scale Dispersion Entropy,CMDE)是DE的改进,进行多尺度处理,能从更多尺度下对时间序列的复杂性进行分析[20]。复合化能克服多尺度散布熵的缺点,能结合多个粗粒化序列的信息,降低熵值的标准偏差使熵值更可靠。针对生物组织在一定温度下逐渐产生变性的特性,GK模糊聚类可以根据输入特征产生一个聚类中心,根据特征对聚类中心的隶属度判断输入特征属于哪一类,因此可以判断生物组织是否变性。

通过上述分析,本文提出了MIVMD-CMDE-GK模糊聚类的生物组织变性识别方法。将采集的超声背散射信号进行MIVMD重构,计算重构信号的CMDE,并将得到的所有CMDE作为特征参数通过GK模糊聚类得到两个聚类中心,计算熵值与聚类中心的贴近度,根据贴近度的大小判断生物组织是否变性。实验结果表明,本文所提的MIVMD-CMDE-GK方法有效提高了超声背散射信号对生物组织变性识别的能力,为超声治疗诊断提供了参考。

1 原理与方法

1.1 模态分解

1.1.1 变分模态分解

VMD算法中,原始信号分解得到的IMF为调频-调幅信号,表达式为:

uk(t)=Ak(t)cos[φk(t)]

(1)

(2)

式中:uk(t)为VMD分解得到的第k个IMF,Ak(t)为瞬时幅值,φk(t)为瞬时相位,ω′k(t)为瞬时频率。

VMD计算过程中,不断更新IMF的中心频率和带宽,在各个IMF的带宽和最小时停止计算,且各IMF之和为原始输入信号。约束变分问题函数如下:

(3)

式中:{ωk}={ω1,ω2,…,ωk}为IMF的中心频率。通过使用增广拉格朗日函数对约束变分问题进行求解,如式(4)所示:

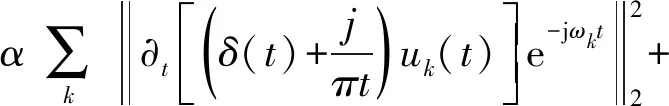
(4)

式中:α为二次惩罚参数,λ(t)为拉格朗日惩罚算子。使用交替方向乘数法求解式(4)的鞍点,同时更新uk,ωk,λ三种参数。将原始信号x(t),通过VMD分解成k个IMF的方法如下[21]:

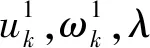
②更新uk,ωk,λ:

(5)

(6)

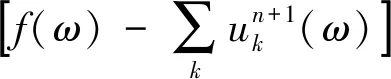
(7)

③设置精度ω,满足当式(8)时,输出结果uk。否则重复②步。

(8)

1.1.2 多迭代变分模态分解

由于噪声频率分布范围广,而VMD分解重构得到的模态数有限,因此得到每个IMF中都含有噪声。为了更好的将信号中的噪声滤除,提出了MIVMD,通过多次选择有用信号能量占比高的分量重构,达到滤除噪声的目的。MIVMD计算方法入下:

①对输入信号进行VMD分解,IMF数为k。

②计算各IMF中的主频能量占此IMF能量的比,能量比越大说明噪声信号越少。

③将能量比小的IMF分量滤除,使用剩余分量重构信号。

④计算重构信号的频谱能量,计算最大的前k-1个频谱能量占重构信号总能量的比。

⑤设定占比阈值,当能量占比小于阈值时,将重构信号视为输入信号并重复步骤(1)～步骤(4)。当能量占比大于阈值时,停止迭代,输出重构信号。

1.2 复合多尺度散布熵

对长度为N采集信号x(t),计算信号的DE如下[22]:

①通过正太分布函数,将采集信号x(t)映射成y(t)

(9)

式中:σ为标准差,mean为采集信号的平均值。

②将y(t)映通过式(10)映射成到1至c的集合z(t),c为类别数。

zc(t)=round[cy(t)+0.5]

(10)

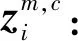
(11)

④每种分散模式的概率为:

(12)

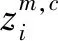
⑤计算DE:

(13)

CMDE是对DE的改进,先对原始输入信号x(t)进行粗粒化尺度因子为τ的处理,得到第K个粗粒化序列:

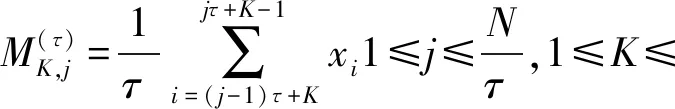
(14)

然后对得到的τ个粗粒化序列散布熵求均值,得到该粗粒化尺度因子下的CMDE为:

(15)

1.3 GK模糊聚类

GK模糊聚类是一种距离协方差矩阵能自适应动态度量的模糊聚类算法,假设输入的特征为B={b1,b2,…,bN},GK模糊聚类的目标函数为[23]:

(16)

可以得到e个聚类中心Oi(i=1,2,…,e);f为模糊指数,模糊指数会影响聚类效果,f太大会导致各类之间相互重叠;U为隶属度矩阵U=[μij]e×N;μij表示第j个元素隶属于第i类的隶属度且满足:

(17)

Dij表示第j个元素与聚类中心Oi的距离泛数:

(18)

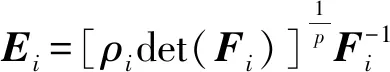
(19)

常用拉格朗日乘法对GK模糊聚类的目标函数进行优化,得到最小值点(U,V),其必要条件为:

(20)

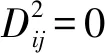
(21)

1.4 评价参数

为了便于比较不同方法的去噪效果,使用信噪比和均方根误差来进行评价。

信噪比:

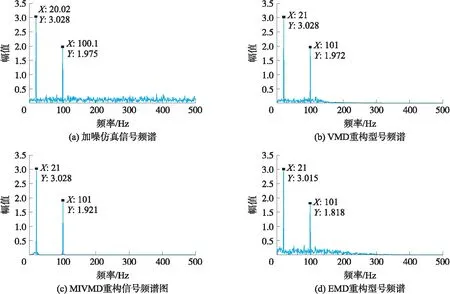
图1 仿真信号与重构信号的频谱对比

(22)

Ps,Pn分别代表有用信号和噪声的有效功率。信噪比越大说明去噪效果越好。

均方根误差:

(23)

signal′,signal,l分别为重构信号、未加噪信号、信号长度。均方根误差越小说明去噪效果越好。

本文采用划分系数PC、划分熵系数PE和Xie-beni指数评估聚类效果[24]。PC,PE均与隶属度矩阵有关,当PC越接近1与PE越大接近0时,聚类的效果越好。XB是用来评估类间距离的一种指数,值越小,聚类类间距离越大,聚类效果越好。

划分系数PC:

(24)

划分熵系数PE:

(25)

Xie-beni指数表达式为:

(26)

式中:θ为类的平均方差,Jmin是类间最短模糊距离。

2 实验分析

2.1 信号去噪

使用VMD、MIVMD、EMD,分别对加噪信号进行重构分解。未加噪仿真信号为x(t)=3sin(40πt)+2sin(200πt),加噪仿真信号为Q(t)=x(t)+η,η为高斯白噪声。对加噪仿真信号分别进行VMD分解重构、MIVMD分解重构并与EMD分解重构进行比较。图1(a)为信噪比为2.31 dB时加噪仿真信号频谱图,图1(b)～1(d)分别为VMD,MIVMD,EMD三种方法重构信号的频谱图。从图1可以发现,EMD和VMD均能抑制中高频噪声,但是对两个有用频率之间的噪声抑制效果较差。而本文提出的MIVMD不仅能抑制中高频噪声,还能有效地抑制两个有用频率之间的噪声。

为了验证MIVMD对低信噪比信号有更好的滤波能力,使用EMD、VMD和MIVMD对信噪比不同的仿真信号进行重构,并计算重构信号的信噪比和均方根误差如图2所示。由图2可知,MIVMD重构信号的信噪比高于EMD与VMD重构信号的信噪比,MIVMD重构信号的均方根误差低于EMD与VMD重构信号的均方根误差。同时可以发现,VMD与EMD重构信号的信噪比随输入信号信噪比增加而增加,而MIVMD在计算过程中,对各个IMF分量的能量进行了分析,因此MIVMD重构信号的信噪比在某一定值附近浮动。

图3(a)、3(b)分别为通过光纤水听器采集的正常与变性组织的超声背散射信号,使用MIVMD对采集的超声背散射信号进行分解重构,模态数设定为5,结果分别如图3(c)、3(d)所示。可以观察到通过MIVMD重构获得的回波信号有明显的脉冲波形,且波形震荡衰减。

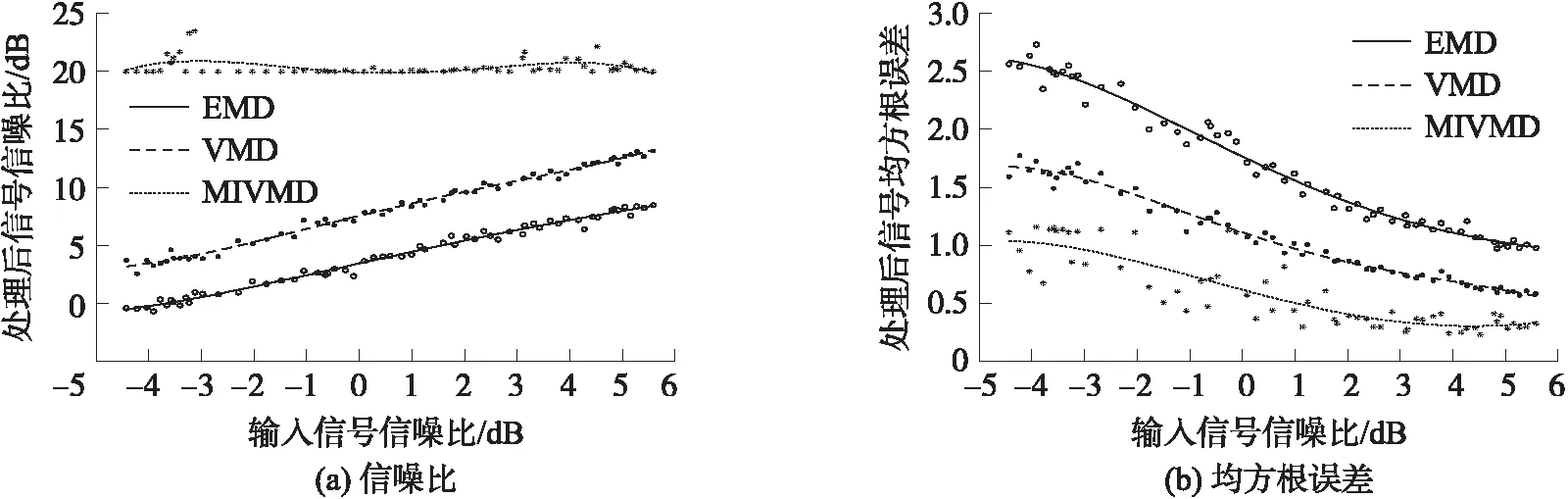
图2 不同输入信噪比下不同方法的去噪效果比较

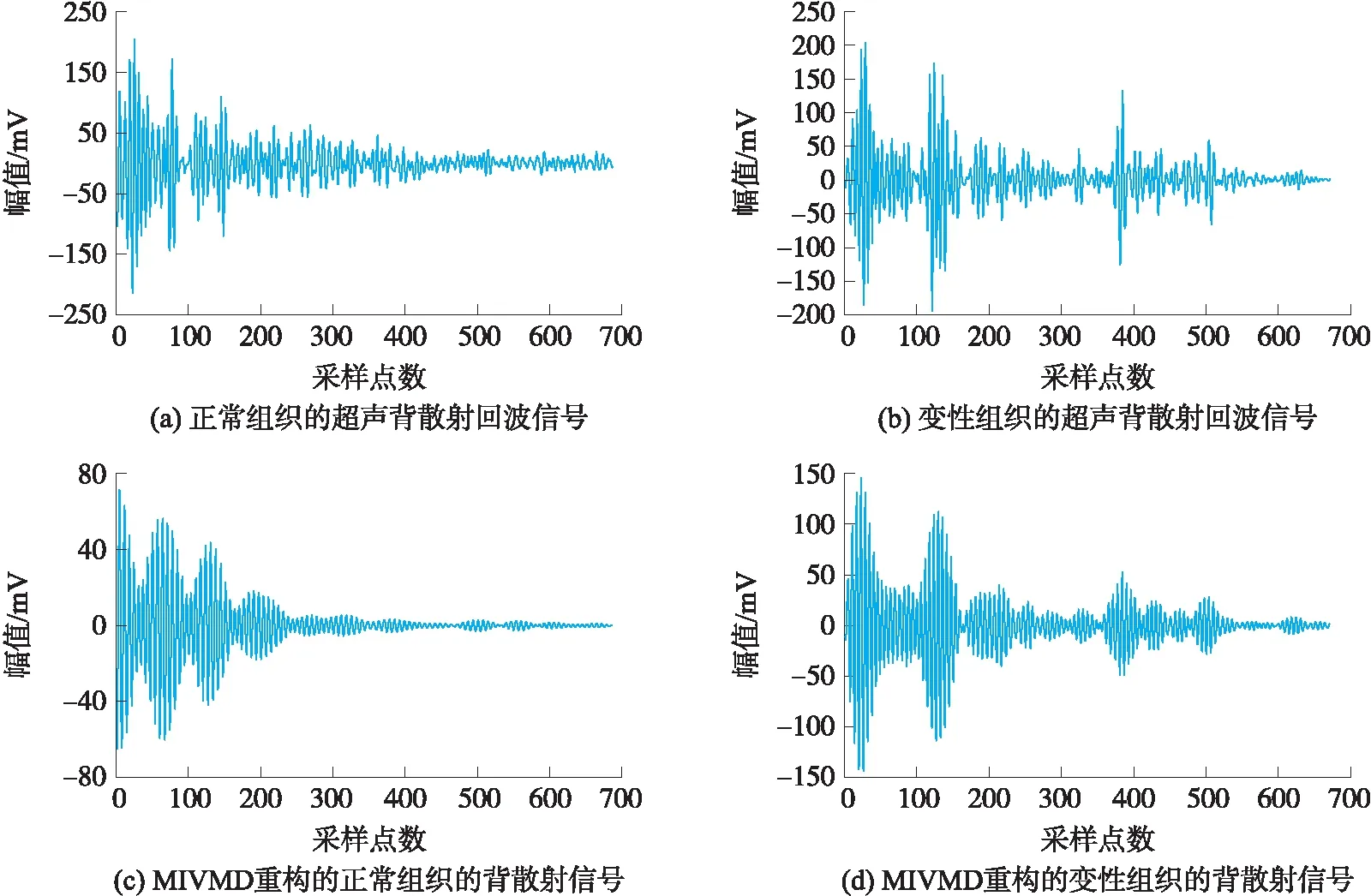
图3 超声背散射回波信号

2.2 变性识别

为了验证本文提出的生物组织变性识别方法的有效性,本文将该方法的判定结果与实际切片判断结果进行比较。实验使用HIFU对新鲜离体猪肉组织辐照来改变生物组织特性,使用热敏电阻测量声焦域处的生物组织温度,最大温度在90 ℃以内;考虑到HIFU环境中强超声的影响,使用光纤水听器(FOPH2000;RP acoustics)获取监控超声的回波信号,并经数字示波器(Model MDO3032;Tektronix)转化为数字信号后进行保存。采集了16组样本共288例实验数据。为找到CMDE的最佳尺度,研究了3到20尺度下,第一组样本的超声背散射信号。为验证MIVMD处理能使提取的特征参数更加有效,使用CMDE对经VMD和MIVMD处理的重构信号进行分析。在使用CMDE进行分析时,为了避免将所有数据视为一种散布模式,需要将类别数设定大于1,本文将变性与未变性组织的信号视为两种类别,因此设定类别数为2。计算CMDE时散布模式数应小于信号长度,而信号进行粗粒化处理将会减少信号长度,为了在分析不同尺度下CMDE时不受维数影响,将维数设定为2。设定延时是为了从不同时间分辨率下对信号进行分析,但延时过大时,信号的有用信息会被丢失且产生混叠,通过比较将CMDE的延时设定为2。

由图4(a)可以发现,使用VMD-CMDE方法得到的变性与未变性组织熵值之间存在差值,但是在尺度为6、16、19时变性与未变性组织熵值之间的差值小。通过图4(b)可以发现,由MIVMD-CMDE得到的变性与未变性组织熵值差值比VMD-CMDE方法得到的熵值差值大,在尺度8到11时,变性组织与未变性组织的熵值差较大,其中在尺度为9时差值最大。经过上述分析,经过MIVMD重构的实际超声背散射信号的CMDE值能用于识别生物组织变性识别。

为了证明尺度为9时CMDE能较好的区分变性组织与未变性组织,分别计算了尺度为9时,经MIVMD处理的16组实验的变性组织与未变性组织的超声回波信号的CMDE均值。同时与文献[16-18]中的近似熵(Approximate entropy,ApEn)、样本熵(Sample Entropy,SE)、模糊熵(FuzzyEntropy,FE)进行比较。如图5所示,可以发现,部分样本组的SE与ApEn中出现变性时的熵值比未变性时的熵值小。所有样本组的变性与未变性的FE不存在交叠,但是部分样本组的变性与未变性的熵值差较小。所有样本组的变性与未变性的CMDE值不存在交叠;相较于FE,变性与未变性的CEMD差值较大。变性组织的超声回波信号的CMDE均值比未变性组织的超声回波信号的CMDE均值高出0.110 8,约为8.12%。

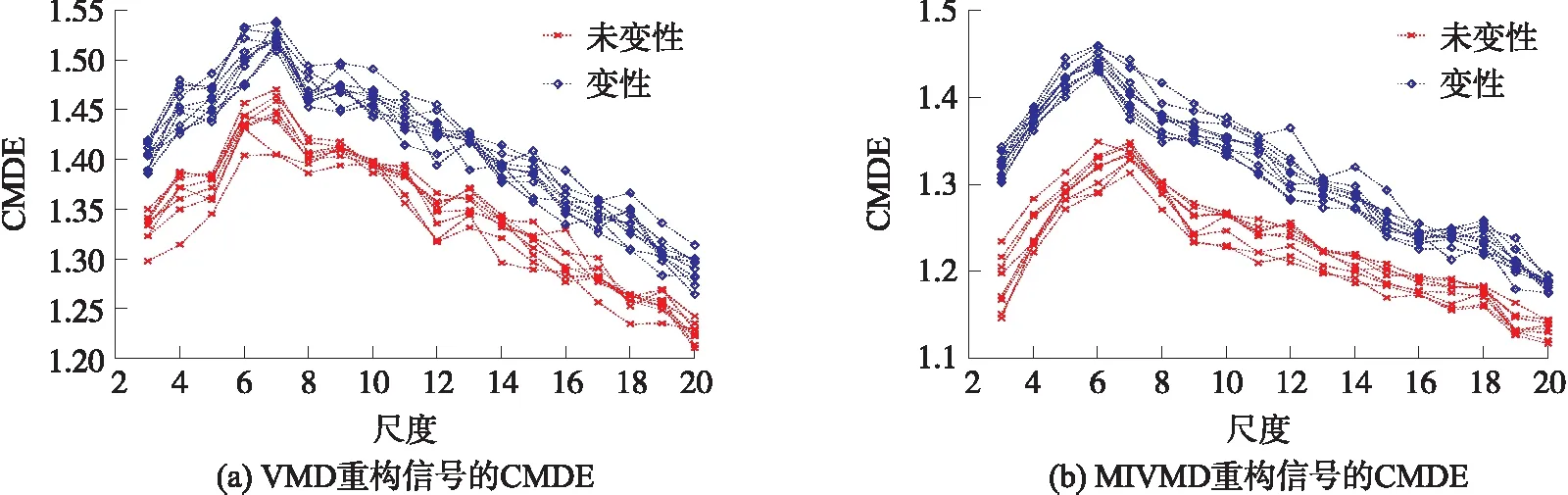
图4 不同信号处理方式时尺度对CMDE值的影响

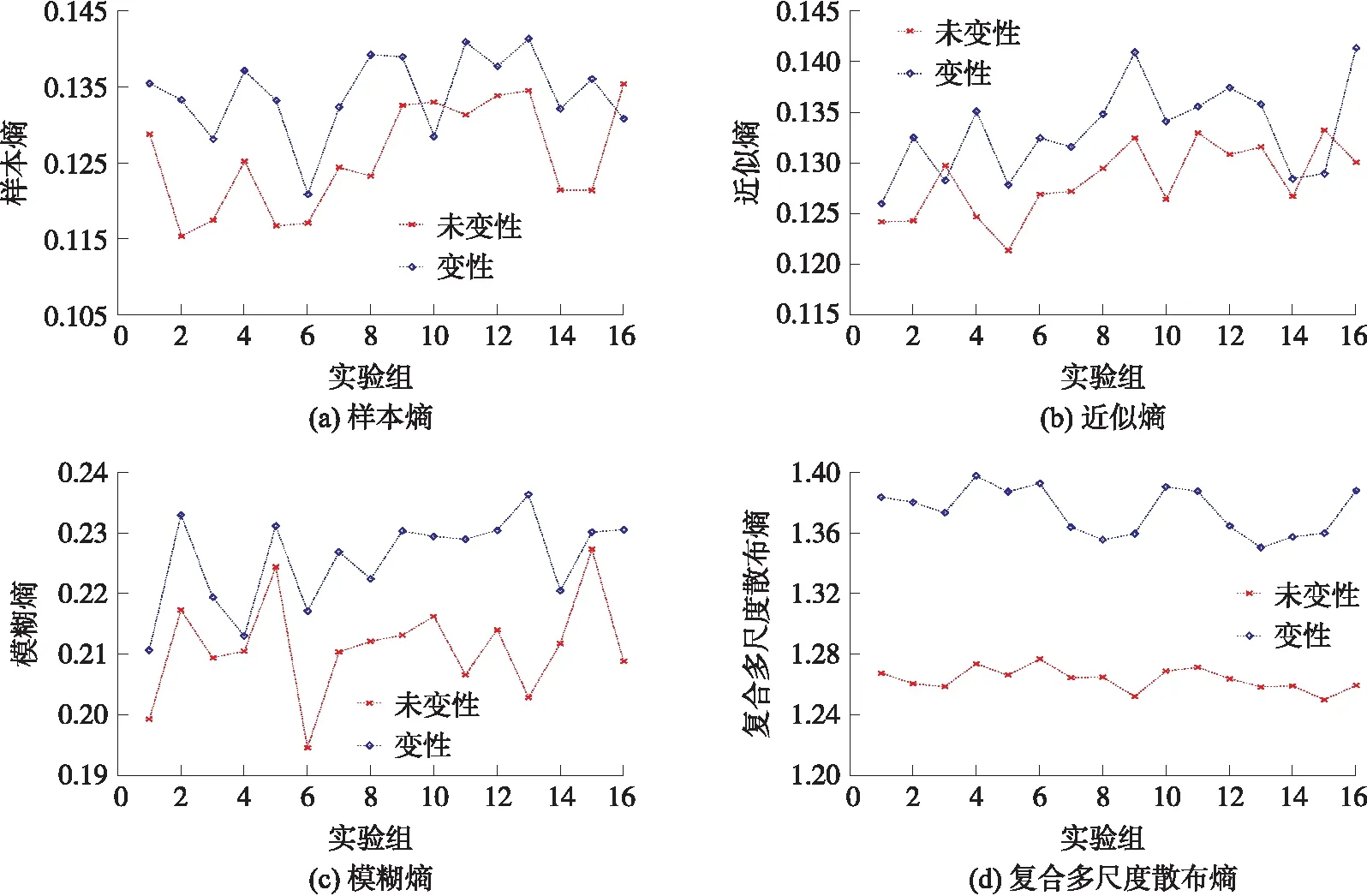
图5 变性与未变性组织的回波信号的不同熵

将所有特征参量视为未知参量进行GK聚类得到未变性与变性两个聚类中心,计算CMDE与两个聚类中心的贴近度,根据贴近度判断样本是否变性,并分别计算MIVMD-SE-GK、MIVMD-ApEn-GK、MIVMD-FE-GK和MIVMD-CMDE-GK四种方法的PC、PE、XB及变性识别率,结果如表1所示。

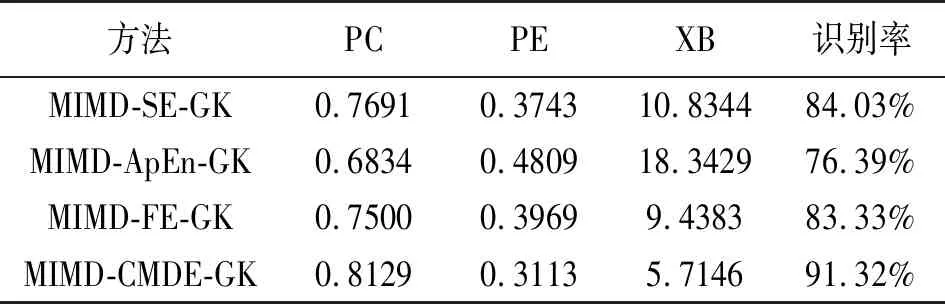
表1 特征参数对聚类效果的影响

通过对MIVMD-SE-GK、MIVMD-ApEn-GK、MIVMD-FE-GK和MIVMD-CMDE-GK方法分析可以发现,MIVMD-ApEn-GK方法的PC指数最小且PE指数最大,聚类划分在四种方法中最模糊,XB指数最大说明MIVMD-ApEn-GK方法的类间分离最小,聚类离散程度最大。与MIVMD-ApEn-GK方法相比,MIVMD-SE-GK和MIVMD-FE-GK方法的PC、PE、XB评价指数都有所改善。在四种方式中,MIVMD-CMDE-GK方法的PC指数最大且PE指数最小,聚类划分在四种方法中最清晰,XB指数最小说明MIVMD-CMDE-GK方法的类间分离最大,聚类离散程度最小。在四种方法中,MIVMD-CMDE-GK方法的识别率最高,说明CMDE对变性生物组织的识别能力比ApEn、SE、FE要强。

3 结论

超声治疗中采集的超声背散射信号含有大量的噪声,且噪声频率范围广,对判断生物组织是否变性造成了影响。针对上述问题提出了MIVMD,同时采用了CMDE算法对超声背散射回波信号进行特征提取并结合GK模糊聚类进行生物组织变性识别。通过仿真和实例验证可以得到一下结论:①MIVMD分解重构的去噪能力比EMD和VMD更好。②利用CMDE对处理过后的超声背散射信号进行了特征提取,结果表明:当延时、类别、嵌入维数均设定为2时,变性组织超声背散射信号的熵值要高于未变性组织超声背散射信号的熵值。经MIVMD处理的超声背散射信号的CMDE值在尺度为9时两者差别最大。③对MIVMD分解重构处理的超声背散射信号进行SE、ApEn、FE和CMDE特征提取并进行GK聚类发现,CMDE有更好地表征生物组织是否变性的能力。