快递员最优送货路线研究

张东翰，赵锐

（商洛学院 数学与计算机应用学院，陕西商洛 726000）

现今，各种购物网站应有尽有，人们在家就可以购买各种生活用品，这给广大消费者带来了便利，也为快递公司的发展提供了机遇。然而，放眼于当今中国快递行业的发展，送货效率的高低已成为快递公司生存与发展的决定因素之一，送货路线的选择是影响送货效率的主要因素之一，快递公司要想在巨大的竞争潮流中站稳脚跟，获得更多的效益和长远的发展，必须在一定的硬件条件下，巧妙地借助信息技术和数学方法，为其快递员制定一套具体可行的送货路线方案。对于最优路线的研究，目前已有许多专家学者做了大量的工作，包括模型的建立，计算方法的改进和问题的变形与推广。大多数研究都是利用中国邮递员问题的知识建立相关的模型，并对路线优化给出了许多不同的算法，例如，贪心算法，匹配算法，动态规划算法和构造法等[1-9]。本文以商洛市商州区为研究对象，根据中国邮递员问题的相关理论[10-11]，对送货员的送货路线进行了研究，得到了商州区快递员送货的最优路线，同时也为其他区域的最优路线研究提供了理论参考。

1 商州区主要街道分布

通过对商州区人口密集分布的街道进行研究和分析，得知商州区繁华的街道有文卫路，团结路，西街，东街，西背街，东背街，中心街，工农路，西关，东关，金凤路，假定送货点分布在各个道路上的，可将快递员送货路线必须经过送货点的问题转化成经过送货点的所在道路的问题即快递员必须经过他负责区域的所有路线，以最快的速度完成所有的送货。对于这个问题的研究，仅以中心广场区域为例进行路线优化研究。

2 快递员送货路线问题分析

本研究利用谷歌地球软件将快递公司所管辖的区域各街道绘制出来，并结合百度地图测距工具以及谷歌地球的测量功能将实际长度测量出来（如图1 所示），再在考察路线的实际情况的基础上，运用相关的求最短路的方法对路线进行优化，最终得出快递员送货的最优路线。

图1 快递员最优路线问题分析流程图

3 模型建立

3.1 模型假设

结合商州区快递员送货的特点，仅以商州区中心广场这个区域为例建立模型，建立模型前有以下假设：

1）假设该区域内快递员的送货点（即接收人的接收点）在各条路线上是均匀分布的。

2）假设该区域快递员的送货量在配送车的车载量以内。即快递员从起点出发，走完所负责区域的所有路线，完成所有的送货量。

3.2 实际的路线转化成平面图形

3.2.1 实际的道路信息转化成虚拟的平面图形

忽略各个道路的宽度，形状，将它抽象成直线，将各个道路的交叉点同样抽象成一个点，使整条路拆分成不再有交叉口的平面图。对于弯曲的街道，可以根据实际情况将它拉伸成一条直线或者转化成一个点。比如，中心广场这块道路的信息处理，由于中心广场是一个圆盘，圆盘连接北新街东段，北新街中段，中心街和和平路四个方向的道路，为了方便计算，将中心广场抽象成一个点，将中心广场与四条道路的交点延长交汇成一点（以两旁的圆盘实际长度的平均值增加到该道路中）。

3.2.2 测量距离

利用谷歌地图软件和百度地图将路线绘制并测量出来，再在增加路线长度的基础之上，就可以得到图2 和图3 所示的路线赋权图。

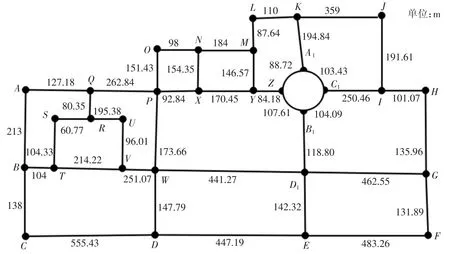
图2 含中心广场的赋权路线图

3.3 路线模型分析

如果只考虑快递员送货的路线，解决此问题的方法是将问题转化成中国邮递员问题来求解。在图3 中，快递员无论在那个点出发，只要经过所有的路线至少一次，并且所走的路线总路程最短。因此，快递员的出发点，快递公司可根据自身的具体情况可任意选一点。

经过对问题的分析，可以将快递员送货路线模型的研究转化为对解决带有附加条件的中国邮递员问题的研究。因此，本研究内容可以用图论语言叙述为：在路线赋权图G 中，寻找一条回路c，使c 包含的每条边至少一次且回路c 的长度最短。

如果此非负赋权图G 是欧拉图，则只要找出它的欧拉环游，就得到了最优路线。如果非负赋权图G 不是欧拉图，即图G 中有奇度数结点，可以通过添加重复边的方法，使图G 扩充为一个欧拉图G*，并且使得图G 中各边的权值和尽可能的小，可用Fluery 算法求出G*的欧拉环游，从而得出最优路线。

图3 简化后的赋权路线图

4 模型求解

4.1 赋权路线图转化成欧拉图

在问题分析中，可知解决快递员最优送货路线问题的思路可分为两种情况：一种是图G 中没有奇度数结点，此时图G 是欧拉图。欧拉环游就是最小的送货路线。另一种是图G 中含有奇度数结点，如果图G 有两个奇度数结点时，找出这两个点间的最短路并加入图G 中，此时得到的图为欧拉图，图中的欧拉环游就是最小送货路线，如果图G 中的奇度数结点大于两个时，需要对这些奇度数结点进行配对，将这些奇度数结点（奇度数结点的个数为偶数）间的最短路加入图G 中，得到的欧拉图中的欧拉环游就是快递员最小的送货路线。

通过对简化后的赋权路线图（图3）的分析，发现具有奇度数的结点有12 个，分别为B 点，T点，V 点，D 点，E 点，G 点，I 点，K 点，M 点，Y 点，N点，X 点。图G中有大于两个奇度数结点时，存在奇度数结点两两配对的方案共有显然，用原始的计算两两点间距离的配对办法工作量巨大，不科学。因此，采用在图3 中加边的方法对这12 个点进行配对。具体方法如下：

1）将这12 个点人工进行初步配对，配对的原则是寻找距离最近的两点进行连接，比如离B点最近的点是T 点，依据此法将剩下的10 个点配对，配对的结果如图4 所示。

2）初步配对好后，在含有配对两点的最小欧拉圈中比较其权值是否小于其它几条权值和的一半。如果小于，将这两点的配对先确定下来。如果大于，将这两点的配对去掉，把连接这两点剩余的几条边相连接，再用这一步的方法进行判断，直到完成最终的配对。此时得到的12 个点的连接就是遍历这12 个点的最短路，最终配对的结果如图5 所示。

由图5 可知，送货路线添加了8 条重复弧。根据Dijkstra 算法可以验证，这8 条弧是经过12个奇度数结点最短的路径。

4.2 Fleury算法

步骤1：令图G 中所有点的集合为V(G)，所有边的集合为E(G)，在V(G)中选任意一点v0,w0=v0。

步骤2：设途径已经选定，则wt=v0v1v2…vt从E(G)-E(W)中选取一条边 ei+1，使得 ei+1与 vi相关联，且除非已经没有选择的余地，否则不要选E(G)-E(W)的割边。

步骤3：反复的执行第二步，直到所有的边都被选到为止。如此得到的wt=v0v1v2…vt就是图G的欧拉环游。

需要注意：按照Fleury 算法寻找欧拉环游时，首次从起点出发，每次选定的下一个点尽量是没有被选过的点，直到选完所有的点第一次回到起点。然后再从起点出发按照此方法，直到所有的边都被选完，最终回到起点。

图4 人工初步配对后的赋权图

图5 赋权路线图转化成欧拉图

4.3 最优路线方案

假设快递员送货的起点在I 点。因此，利用Fleury 算法步骤得到图5 的欧拉环游为：W=IZKMYXNPQBTVDWD1EGD1ZIGD1EDBTQVWPXNMYZKI。

将上面找到的欧拉环游还原到图2 中，得到了中心广场区域快递员最优送货路线的方案是：

从宏影路与北新街东段的交汇处（起点）—中心广场东侧—宏影路—和平路—金凤路—金凤路与北新街中段的交汇处—北新街中段—北新街中段与迎宾路的交汇处—迎宾路—府前路—府前路与人民路的交汇处—人民路—人民路与北新街中段的交汇处—北新街中段—北新街中段与文卫路的交汇处—文卫路—文卫路与团结路的交汇处—团结路—团结路与工农路的交汇点—工农路—西关与西街的交汇处—工农路—工农路与西背街的交汇处—西背街—西背街与中心街的交汇处—中心街—西街与东街的交汇处—东街—东环路—东环路与东背街的交汇处—东背街——东背街与中心街的交汇处—中心街—中心广场的西侧—中心广场的东侧—宏影路与北新街东段的交汇处（起点）—北新街东段—东环路—东环路与东背街的交汇处—东背街—东背街与中心街的交汇处—中心街—中心街与西街的交汇处—西街—西关—西关与文卫路的交汇处—文卫路—团结路与文卫路的交汇处—团结路（从文卫路与团结路交汇点向东走第一个路口）—苏尚巷与北新街中段的交汇处—苏尚巷—团结路（从文卫路与团结路交汇点向东走第二个路口）—团结路—工农路与团结路的交汇处—工农路与北新街中段的交汇处—北新街中段—北新街与迎宾路的交汇处—迎宾路—府前路—府前路与金凤路的交汇处—金凤路—北新街中段—中心广场西侧—戏乡巷—戏乡巷与和平路的交汇处—戏乡巷—北新街东段—宏影路与北新街东段的交汇处。

5 结语

该模型以商洛市商州区为研究对象，从实际问题出发，容易理解与灵活应用，不仅可以为快递员节省送货时间，降低送货成本，减轻快递员每天的工作量，使快递公司的运行更加高效，更能带动商州区的经济发展，具有一定的实用性和较强的推广性，而且也为现实中其它路线优化提供了一定的理论基础和参考依据。