基于双边函数全局运动模型的海冰漂移监测方法
徐嘉 张绪冰 王凯
(1 北京空间飞行器总体设计部,北京 100094)(2 中国地质大学(武汉)地理与信息工程学院,武汉 430074)
大面积海冰对海上航运安全等方面产生重要的影响,常导致海港封港、船舶损坏、航道阻塞、海洋工程设施损毁等问题,在海冰密集度较高的海域,尤其是南北极区,缺乏对海冰漂移的监测,将难以获取海冰的快速运动变化情况,使得船舶受困于密集的浮冰区[1-2]。因此,研究海冰漂移监测方法,对实时掌握海冰漂移的状态,提高海冰运动的分析与预报能力,具有重要的价值[3-4]。
相较于数值模拟和浮标观测海冰漂移监测方法受到场地限制等影响[5-6],采用卫星遥感方式对海冰漂移进行监测,具有探测范围广、实时性强、周期性监测等优势;尤其是合成孔径雷达(SAR)成像模式,不受云雾、雨雪等恶劣天气条件的干扰,同时具有多极化、多波段、透射性强等优点受到广泛的关注[7-9]。
目前,在海冰漂移遥感监测的方法研究方面,普遍采用最大互相关(Maximum Correlation Criterion, MCC)[10]方法,光流法[2,11]、特征点匹配等方法[12-13]进行海冰漂移运动的监测。MCC方法受影像噪声影响较大,在海冰发生旋转与形变状态下误差较大;光流法通过计算每一个像素的光流移位来近似得到一个密集的速度场,该方法对时间分辨率较低或信噪比较低的图像不适用,且在计算过程中反复的迭代,使得计算量较大,效率不高。基于特征点匹配的方法可以通过一定量的匹配特征点计算海冰的运动场,可以有效减少计算量,提高检测效率,并且对于尺度缩放、灰度变换,以及一定的图像形变具有较好的鲁棒性。目前普遍采用经典的尺度不变特征变换(Scale Invariant Feature Transform,SIFT)算法进行不同时相的海冰遥感影像特征点匹配,但是,在实际的应用研究中发现,采用SIFT方法进行海冰漂移监测,存在较多的误匹配点,在采用随机采样一致(RANSAC)等误匹配剔除方法后,仍然会有一些误匹配点导致海冰漂移计算的误差。
针对上述方法存在的问题,本文基于SAR影像,采用全局运动模型双边函数(Bilateral Functions for Global Motion Modeling,BFGMM)算法,进行海冰漂移运动的计算。该算法基于分段光滑函数描述模板图像与匹配图像之间的全局性约束运动模型,避免了仿射变换、非线性薄板样条函数等模型在剔除误匹配点同时,破坏了模型函数的全局属性的问题,能够实现特征点的精确匹配[14]。对北冰洋边缘海波弗特海域海冰哨兵1号(Sentinel-1)SAR影像进行了海冰漂移速度矢量场的计算。
1 双边函数全局运动模型方法
1.1 模型的概述
针对海冰漂移运动的计算,基于海冰SAR影像之间特征点的匹配,属于一个基本的视觉计算问题,研究人员通常关注那些鲜明的、易于匹配的离散的特征点,尽管目前在图像匹配领域经典描述方法有SIFT、加速顽健性特征算法(Speeded-Up Robust Features, SURF)以及相关的改进算法如主成分分析-尺度不变特征变换(Principal Component Analysis SIFT,PCA-SIFT)、梯度定位方向直方图(Gradient Location-Orientation Histogram,GLOH)、独立成分分析-尺度不变特征变换(Independent Component Analysis-Scale Invariant Feature Transform, ICA-SIFT)等,但是它们仅仅基于局部信息的对应关系仍然容易出现不稳定和匹配异常的现象。一些适合全局参数化的方法,只能在诸如静态场景中不同视角图像的仿射变换,以及针对光滑形变的非刚体的薄板样条等特定的图像运动变换模型下取得一定的成功,并在运动模型的约束下,借助于随机采样一致(RANSAC)方法进行误匹配(外点)的剔除。为图像配准建立一个通用的运动模型是困难的,不仅匹配点分散而且存在噪声,还可能出现大量的运动不连续问题,因此建模需要检测和改变运动边界的参数化,然而仅仅关注建模的运动方面,将会丢弃大量的信息,这增加了一般模型的脆弱性,同时也限制了模型的鲁棒性。
双边函数全局运动模型采用分段光滑函数作为稳健的全局性约束,集成处理模型拟合、误匹配剔除,匹配集扩展等问题,实现图像的配准。所谓双边函数,即通过将期望输出作为函数域的一部分以达到平滑的目的,称之为双边函数。双边域基于尽可能平滑的传统数据模型采用全局函数拟合空间分段光滑运动数据,并通过最小化全局代价函数实现上述计算。全局光滑性使得双边运动模型计算具有很强的鲁棒性和高精度,无需随机采样一致(RANSAC)假设和检验框架,计算模型能有效验证新的匹配假设,实现大量的特征点匹配,同时将误匹配概率降为最小值。
1.2 模型的原理
针对一个非刚体运动拟合问题,即求出与给定数据集一致的最光滑的函数fk(Po),其中Po表示图像像素坐标,fk(Po)表示像素的移动。光滑性(无限可微性)意味着连续性的约束,即[14]
(1)
式(1)使得像素Po邻域的函数值相似,该模型导致不连续的运动边界处产生较大的误差。双边函数全局运动模型将fk(Po)函数的域改进为空间维和运动维的双边域,对像素Po的空间进行重新定义,P=[xyuv]T,使得空间域内的不同速度的像元点将不再毗邻,这样在保持函数fk(P)平滑约束的同时,可以赋予在空间坐标上相邻的像元不同的函数值。如果P的域中的两个像元点之间的运动差趋近于无穷大,那么两个像元点的分离度也趋近于无穷大,降低了像元彼此之间的影响。这样,无论像元的空间坐标如何,在像元运动空间的不连续值增加时,双边域的平滑度惩罚项不会趋近于无穷大。
将像素P的运动表示为m=[uv]T,针对待匹配的两幅海冰影像,定义集合N={Poj,mj,aj},j为匹配索引,Poj表示像元的空间位置,mj表示像元的运动假设,aj为4×1的向量,表示从局部特征方向导出的相对仿射方向,以下以双边变换仿射为例进行双边函数的具体阐述。
双边变换仿射是一组在双边域上平滑变化的仿射参数集,令P是在D(D=4)维双边域中的一个点,q为标量。不失一般性,仅考虑x方向的运动,给定观测数据如下[14]
(2)
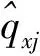
qx(P)=f1(P)x+f2(P)y+f3(P)
(3)
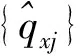
(4)
需要搜索最小代价的fk(P)函数,代价函数表示为
(5)
其中C(·)表示Huber代价
(6)
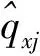
(7)
式中:g(P-Pj,γ)=e-|P-Pj|2/γ2。采用式(7)基于N维向量wk和标量Hk卷积的形式,便可以采用梯度下降的方式计算式(5)最小化能量。式(5)中基于Huber代价的能量可以通过平滑约束忽略一些外点,实现稳健的非参数化的平滑曲线拟合。注意:所得到的式(3)所示双边仿射模型并非一一映射函数,相反,其通过检测(qx-(x+u))2代价来确定匹配空间位置P是否有效。
qy(P)=f4(P)x+f5(P)y+f6(P)
(8)
2 研究区域与数据
本文的研究区域为北冰洋边缘海波弗特海域(Beaufort Sea),位于北纬70°以北,地处美国阿拉斯加州北部和加拿大西北部沿岸以北至班克斯岛之间,北极群岛以西,楚科奇海以东。该区域气候严寒,海面几乎全年冰封,仅在8月~9月沿岸出现狭窄的无冰海面,可以通航。近岸处每年8月、9月间化冻,马更些湾和阿蒙森湾因有来自较低纬度的马更些河等大河注入,无冰海面可宽达100多千米。
采用的影像数据为Sentinel-1数据,Sentinel-1是欧洲雷达遥感卫星,用于全球环境和安全监视(Global Monitoring for Environment and Security,GMES)。Sentinel-1作为一个星座包含两颗卫星,分别是Sentinel-1A和Sentinel-1B在同一轨道平面内,相位相差180°,任务提供了一种可以使用雷达独立连续测绘地图的能力,拥有更高的重访频率,更好的覆盖能力,更好的时效性和可靠性。Sentinel-1任务的总体目标是提供连续的C波段合成孔径雷达遥感应用。该任务的关键设计参数在于重访时间、覆盖性、时效性,还结合了雷达频率谱段、极化方向、分辨率及其他成像质量参数。
本文采用的试验数据如表1所示,总共取了4组影像,每组影像两个不同时相的影像,第一幅为初始海冰模板影像,第二幅为海冰漂移待匹配影像,具体数据的成像时间与经纬度坐标,图1为试验数据在波弗特海域的空间分布示意。
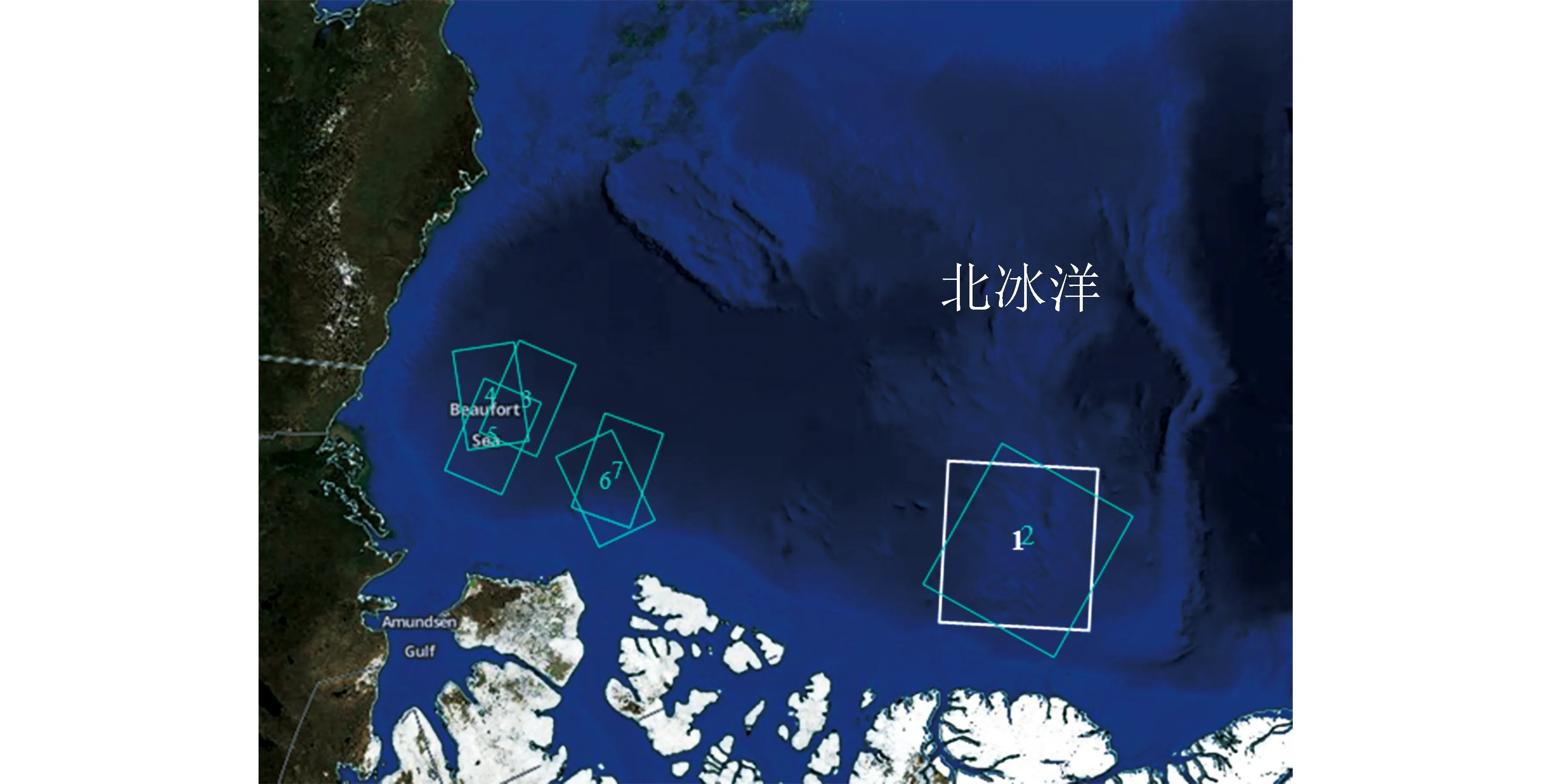
图1 海波弗特海域Sentinel-1试验数据空间分布示意图
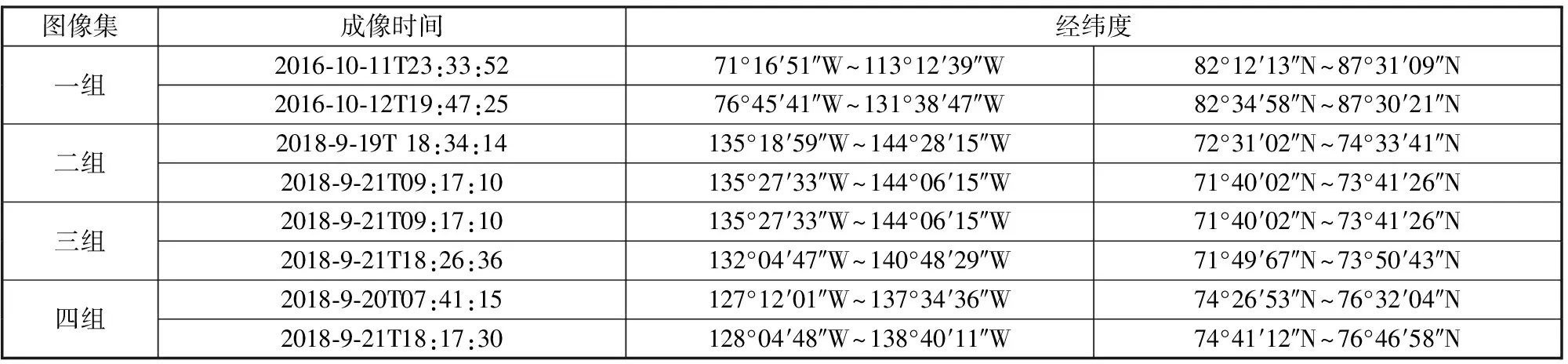
表1 海波弗特海域Sentinel-1试验数据
3 试验结果与分析
3.1 算法精度分析
本文将BFGMM算法与经典的SIFT算法进行对比,基于表1中第二组至第四组数据进行了试验,试验结果如图2和表2所示。通过三组数据的对比试验可以看出,SIFT算法在基于SAR影像的特征点匹配中存在较多的错误匹配,而BFGMM算法则无论从正确匹配的特征点对数量,以及匹配精度上比前者都要高,具体如表2所示:SIFT算法在三组数据上的匹配正确率分别为47.06%,59.29%和98.36%,而BFGMM算法的正确匹配率均超过98%;同时如图2所示,BFGMM算法中即使存在误匹配的特征点对,其绝对误差也相对较小。因此从算法的精度而言,BFGMM算法要优于SIFT算法。
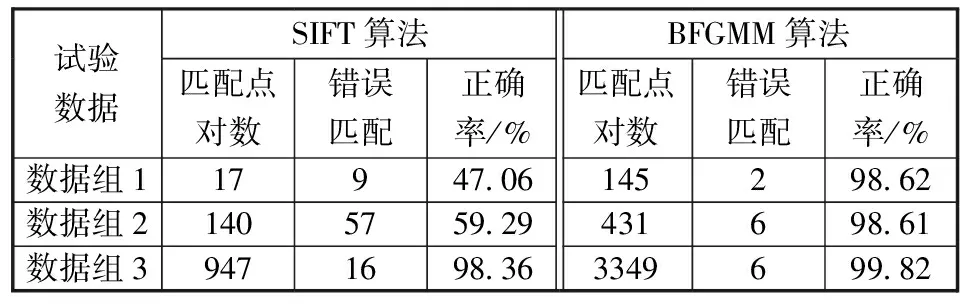
表2 BFGMM算法与SIFT算法特征点匹配精度对比分析



图2 BFGMM算法与SIFT算法特征点匹配精度对比分析
3.2 波弗特海域海冰漂移分析
1)特征点匹配
选取表1中第一组数据进行分析,即2016年10月11日的Sentinel-1影像为海冰初始状态模板图像(71°16′51″~113°12′39″W,82°12′13″~87°31′09″N),2016年10月12日的Sentinel-1影像为海冰漂移后的待配准图像(76°45′41″~131°38′47″W,82°34′58″~87°30′21″N)。模板图像中检测特征点9287个,海冰漂移图像检测特征点9003个。采用BFGMM算法进行特征点匹配,正确匹配点对为1336对。特征点检测及特征点配准结果如图3、图4所示。
图3 波弗特海域海冰图像特征点提取

图4 BFGMM算法特征点匹配结果
2)海冰漂移速度计算
计算匹配点的移动速度,首先计算海冰漂移时间
T=t1-t2
(9)
式中:T为海冰漂移时间,t1为海冰漂移初始影像成像时间,t2为漂移后影像成像时间。本例中海冰漂移初始影像成像时间为2016年10月11日23:33:52,漂移后影像成像时间2016年10月12日19:47:25,海冰漂移时间即为72 813 s。
匹配点的位移量计算公式为
(10)
式中:S为图像像元尺寸,(x1,y1)为海冰漂移前的匹配点坐标,(x2,y2)为漂移后的匹配点坐标。匹配点移动速度V为
(11)
3)海冰漂移速度场空间分布
在海冰漂移速度计算的基础上,依次计算各对匹配点的移动速度,根据移动速度值的大小进行分级彩色渲染,具体如图5所示。其中位移线中的蓝色端点为海冰初始特征点位置,位移线末端为海冰漂移后特征点位置。图5反应了海冰漂移的方向、位移量、速度大小以及漂移速度场空间分布等,由图5分析可知:该区域海冰西南方位运动较快,速度基本大于1.4 m/s,从西南方向往东北方向过渡,漂移速度逐步减缓,中部范围至东北角速度主要处于1.2~1.4 m/s之间,少量局部区域海冰运动速度低于1.2 m/s。

注:红色位移线表示该点处海冰移动速度大于1.4 m/s,绿色位移线表示海冰运动速度在1.2~1.4 m/s之间,蓝色位移线表示该点处海冰运动速度小于1.2 m/s。
图5 海冰漂移速度场空间分布
Fig.5 Spatial distribution of velocity field of sea ice
4 结束语
本文基于双边函数全局运动模型的特征点匹配算法,采用Sentinel-1雷达数据,通过对波弗特海域海冰漂移运动分析,进行了北极所选区域海冰漂移运动的监测研究。全局运动模型双边函数方法基于分段光滑函数描述海冰漂移运动,能够较精确描述运动模型的全局属性,实现海冰漂移前后特征点的精确匹配;此外,采用该方法选取波弗特海域Sentinel-1雷达影像数据进行海冰漂移运动分析,并绘制了海冰运动速度场空间分布图。试验结果表明:采用全局运动模型双边函数方法对极地海冰运动漂移进行分析具有很高的可靠性,该算法针对海冰漂移前后的特征匹配正确率在98%以上,且正确匹配的特征点数量更多,较经典的SIFT等方法有明显提高。该研究可为利用卫星多极化、多波段遥感手段提高极区环境监测能力提供更加准确和高效的方法,对于地球系统观测和科学研究、极区航道利用、海上航运安全、极区自然资源开发以及军事活动等具有重要支撑作用。

