给水管网混沌粒子群优化算法及模型实验研究

王伟伟，车然娜，丁 超，，贺海浪，徐彬彬

（1.安徽建筑大学，合肥 230601；2.安徽省综合交通研究研究院股份有限公司，合肥 230088）

给水管网的设计是城镇国民基础建设，在城镇的建设和发展中发挥着极其重要的作用。 整个给水系统中，给水管网投资占整个工程费用的70%～80%［1］。研究表明，通过优化计算，可节省5%～10%的工程投资［2］。 另外，由于老旧城区给水管网布置不尽合理，使得管网系统优化、改进面临着严峻的问题。因此如何设计一个即科学又经济的给水管网系统具有重要的现实意义。

目前，遗传算法、声搜索算法等智能算法［1-3］都被广泛的应用于给水管网的优化研究中。 但由于存在将算法与具体问题相结合的难点，导致了优化搜索效率低，难以计算高复杂的问题。因此本文提出了一种改进的混沌粒子群算法的管网多目标优化模型，避免了粒子群算法局部搜索能力差的问题，克服了传统管网优化智能算法存在的问题，提高了给水管网优化效率。

粒子群算法（Particle swarm optimization）是一种智能优化的演化算法［4］，操作方便、收敛速度快。 文献［5］运用了PSO结合惩罚函数对单目标管网优化进行了研究，说明了PSO在单目标管网优化问题中的有效性和高效性。但是存在优化目标单一、局部寻优能力差等问题。

1 给水管网优化设计的数学模型

在管网优化设计中，必须考虑水压、水量的保证性、水质的安全性、可靠性和经济性［5］4个方面的问题。本文以经济性和可靠性为目标函数，将其余参数作为约束条件，对管网系统进行优化求解。

1.1 目标函数的建立

1.1.1 经济性目标函数

对于管网经济性，目标函数是管网年用费折算率值最小，对于单水源供水系统可由非线性数学模型进行描述，如式（1）：

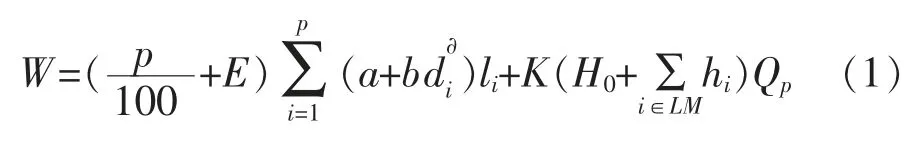
1.1.2 可靠性目标函数

给水系统可靠性是指规定的使用状态下，在规定时间内完成预定功能的性能［6］。 针对给水管网优化模型特点，本文以管网供水量与需水量之比作为管网可靠性的数学表征式，由于不同类型用户的用水标准不同，对用水节点施加一个权重系数ξi，如式（2）：

式中 ξi为用水节点权重；为节点须水量为节点供水量。

1.2 约束条件

水力约束：

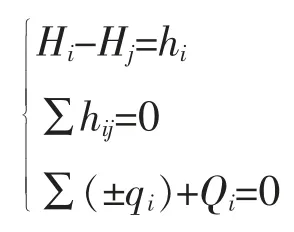
节点水压约束：

式中 Hc为自由水压；Ha为允许自由水压；Hmax为允许最大水压。

流速和管径约束：

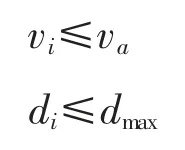
式中 va，dmax分别为允许最大流速、允许最大管径。

2 给水管网优化的PSO原理及改进

针对给水管网多目标优化的复杂性，本文提出了改进的PSO算法，可以提高优化的收敛效率，提高给水管网优化效果。

2.1 PSO原理

文献［6］基于鸟群觅食行为提出了PSO，在PSO中每个优化问题的潜在解都可以想象成搜索空间中的一只鸟，成为“粒子”。粒子追寻当前的最优粒子在解空间中搜索，PSO初始化为一群随机粒子，然后通过迭代找到最优解［7］。PSO广泛的应用于解决单目标优化问题。

假设在N维区域中，粒子群规模为n，xi=（xi1，xi2，…，xiD）是粒子i的位置，vi=（vi1，vi2，…，viD）是粒子i的速度，pi为粒子i的最优位置，pg为全体最优位置。粒子更新如式（3）：

式中 w为惯性权重；c1，c2为学习因子。

2.2 基于PSO的二维多目标搜索算的改进

近年来，多目标PSO得到了各界学者广泛关注，国内外学者已进行了广泛研究，证明多目标粒子群算法在求解多目标优化问题时往往更实用有效［7］。

本文改进了多目标粒子群算法，通过设计不可行域，改进适应度函数的方式，对约束条件进行处理。通过对非劣集（非劣集是指当前新粒子不受其他粒子及当前非劣集中粒子的支配）的筛选、更新，对多目标优化函数进行求解。

2.2.1 约束条件的处理

对于约束条件的处理，是遗传算法、粒子群算法等智能算法应用于给水管网优化设计研究的热点和难点问题，目前大多数研究者采用惩罚函数法来处理约束条件。 然而在研究过程中，对于惩罚因子的确定困难且繁琐。对于多目标PSO算法，运用不可行域对约束条件进行更为便捷、有效处理，搜索空间如图1。

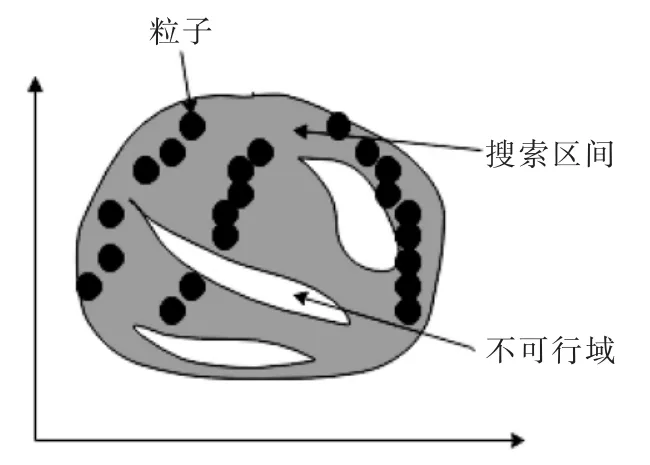
图1 多目标PSO算法原理

考虑到可行空间被割裂，在粒子非劣集更新的时候，对于在不可行区域的粒子，给予一随机选择更新。

2.2.2 改进约束多目标PSO流程

约束多目标PSO算法流程如图2，总体步骤为：

（1）随机产生一个化种群，包括粒子速度、位置，并对粒子最优值进行初始化。

（2）根据约束支配关系初始筛选非劣解。

（3）按指定次数循环迭代：①对惯性权重、学习因子等自适应参数进行调整；②非劣集筛选、更新：当粒子不受其他粒子支配时把粒子放入非劣解集，每次更新前都从非劣解集中随机选择一个粒子作为群体最优粒子。

图2 多目标PSO算法流程

2.3 对于管网PSO混动权重的引入

混沌运动具有的遍历型、随机性等特点，将其结合到粒子群算法，可以有效解决粒子早熟问题，加强搜索效率，提高最优解的精度和收敛速度［8］。 算法流程如图3。

图3 给水管网混沌PSO算法流程

对于本模型，计算如式（4）：

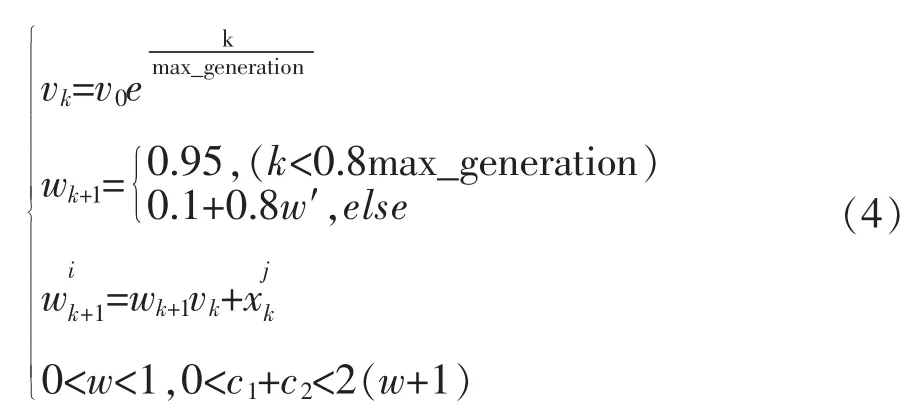
式中 v为速度；x为粒子位置；c1，c2为学习因子。

2.4 基于混沌粒子群算法的给水管网多目标优化模型建立

传统管网优化模型中，仅以经济性作为优化目标，未考虑管网的稳定性，这导致给水管网故障率高，容易影响到居民正常用水。 本文设计目标函数为具体求解过程如图4。

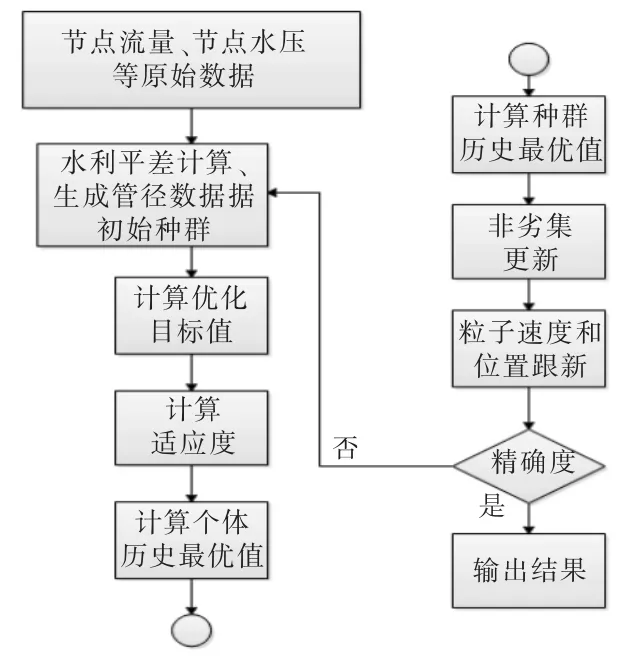
图4 优化模型流程

3 实验模拟

某城市给水管网一个泵站供水，地面相对高度按0.00m计算。设计水量3.2万m/s，要求最小服务水头24m。根据混沌粒子群算法在给水管网优化设计中的应用，对管网进行的优化分析，如图5。给水管网管段与节点信息如表1。

图5 给水管网实例

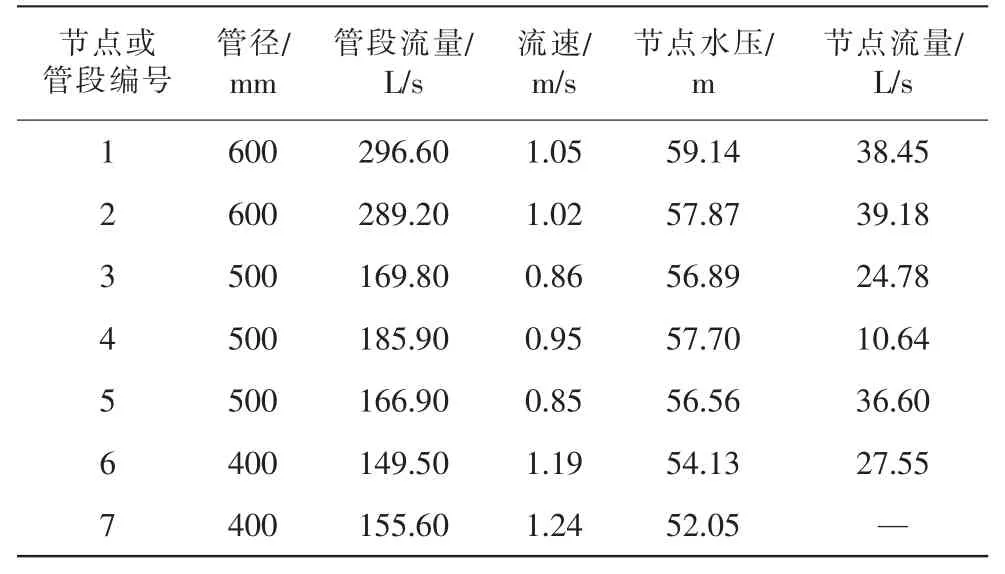
表1 管段与节点信息

最终得优化方案管网设计方案计算得管网年折算费用为329860.472元，管网运行费用462367.569元，管网设计方案计算得总管网年折算费用792228.041元，可靠性计算得0.6601。

4 结语

基于对传统粒子群算法的改进，设计了一种给水管网混沌粒子群优化算法，提高了算法的遍历能力，并且结合多目标优化算法，以经济性和可靠性为目标函数得到了优化结果，得到了较为满意的结果。